NAG Toolbox Chapter Introduction

F07 — linear equations (lapack)

This chapter provides functions for the solution of systems of simultaneous linear equations, and associated computations. It provides functions for

• matrix factorizations;
• solution of linear equations;
• estimating matrix condition numbers;
• computing error bounds for the solution of linear equations;
• matrix inversion;
• computing scaling factors to equilibrate a matrix.

Functions are provided for both real and complex data.

For a general introduction to the solution of systems of linear equations, you should turn first to the F04 Chapter Introduction. The decision trees, in Decision Trees in the F04 Chapter Introduction, direct you to the most appropriate functions in Chapters F04 or F07 for solving your particular problem. In particular, Chapters F04 and F07 contain Black Box (or driver) functions which enable some standard types of problem to be solved by a call to a single function. Where possible, functions in Chapter F04 call Chapter F07 functions to perform the necessary computational tasks.

There are two types of driver functions in this chapter: simple drivers which just return the solution to the linear equations; and expert drivers which also return condition and error estimates and, in many cases, also allow equilibration. The simple drivers for real matrices have names of the form f07_a and for complex matrices have names of the form f07_n. The expert drivers for real matrices have names of the form f07_b and for complex matrices have names of the form f07_p.

The functions in this chapter (Chapter F07) handle only dense and band matrices (not matrices with more specialised structures, or general sparse matrices).

The functions in this chapter have all been derived from the LAPACK project (see Anderson et al. (1999)). They have been designed to be efficient on a wide range of high-performance computers, without compromising efficiency on conventional serial machines.

This section is only a brief introduction to the numerical solution of systems of linear equations. Consult a standard textbook, for example Golub and Van Loan (1996) for a more thorough discussion.

We use the standard notation for a system of simultaneous linear equations: where $A$ is the coefficient matrix, $b$ is the right-hand side, and $x$ is the solution. $A$ is assumed to be a square matrix of order $n$.

If there are several right-hand sides, we write where the columns of $B$ are the individual right-hand sides, and the columns of $X$ are the corresponding solutions.

We also use the following notation, both here and in the function documents:

Inequalities of the form $\left|A\right|\le \left|B\right|$ are interpreted component-wise, that is $\left|a_{ij}\right|\le \left|b_{ij}\right|$ for all $i,j$.

If $A$ is upper or lower triangular, $Ax=b$ can be solved by a straightforward process of backward or forward substitution.

Otherwise, the solution is obtained after first factorizing $A$, as follows.

General matrices (LU factorization with partial pivoting) where $P$ is a permutation matrix, $L$ is lower-triangular with diagonal elements equal to $1$, and $U$ is upper-triangular; the permutation matrix $P$ (which represents row interchanges) is needed to ensure numerical stability.

Symmetric positive definite matrices (Cholesky factorization) where $U$ is upper triangular and $L$ is lower triangular.

Symmetric positive semidefinite matrices (pivoted Cholesky factorization) where $P$ is a permutation matrix, $U$ is upper triangular and $L$ is lower triangular. The permutation matrix $P$ (which represents row-and-column interchanges) is needed to ensure numerical stability and to reveal the numerical rank of $A$.

Symmetric indefinite matrices (Bunch–Kaufman factorization) where $P$ is a permutation matrix, $U$ is upper triangular, $L$ is lower triangular, and $D$ is a block diagonal matrix with diagonal blocks of order $1$ or $2$; $U$ and $L$ have diagonal elements equal to $1$, and have $2$ by $2$ unit matrices on the diagonal corresponding to the $2$ by $2$ blocks of $D$. The permutation matrix $P$ (which represents symmetric row-and-column interchanges) and the $2$ by $2$ blocks in $D$ are needed to ensure numerical stability. If $A$ is in fact positive definite, no interchanges are needed and the factorization reduces to $A=UD{U}^{\mathrm{T}}$ or $A=LD{L}^{\mathrm{T}}$ with diagonal $D$, which is simply a variant form of the Cholesky factorization.

Given one of the above matrix factorizations, it is straightforward to compute a solution to $Ax=b$ by solving two subproblems, as shown below, first for $y$ and then for $x$. Each subproblem consists essentially of solving a triangular system of equations by forward or backward substitution; the permutation matrix $P$ and the block diagonal matrix $D$ introduce only a little extra complication:

General matrices ( LU factorization)

Symmetric positive definite matrices (Cholesky factorization)

Symmetric indefinite matrices (Bunch–Kaufman factorization)

Frequently, in practical problems the data $A$ and $b$ are not known exactly, and it is then important to understand how uncertainties or perturbations in the data can affect the solution.

If $x$ is the exact solution to $Ax=b$, and $x+\delta x$ is the exact solution to a perturbed problem $\left(A+\delta A\right)\left(x+\delta x\right)=\left(b+\delta b\right)$, then where $\kappa \left(A\right)$ is the condition number of $A$ defined by

In other words, relative errors in $A$ or $b$ may be amplified in $x$ by a factor $\kappa \left(A\right)$. Estimating condition numbers discusses how to compute or estimate $\kappa \left(A\right)$.

Similar considerations apply when we study the effects of rounding errors introduced by computation in finite precision. The effects of rounding errors can be shown to be equivalent to perturbations in the original data, such that $\frac{‖\delta A‖}{‖A‖}$ and $\frac{‖\delta b‖}{‖b‖}$ are usually at most $p\left(n\right)\epsilon$, where $\epsilon$ is the machine precision and $p\left(n\right)$ is an increasing function of $n$ which is seldom larger than $10n$ (although in theory it can be as large as $2^{n-1}$).

In other words, the computed solution $\hat{x}$ is the exact solution of a linear system $\left(A+\delta A\right)\hat{x}=b+\delta b$ which is close to the original system in a normwise sense.

The previous section has emphasized the usefulness of the quantity $\kappa \left(A\right)$ in understanding the sensitivity of the solution of $Ax=b$. To compute the value of $\kappa \left(A\right)$ from equation (3) is more expensive than solving $Ax=b$ in the first place. Hence it is standard practice to estimate $\kappa \left(A\right)$, in either the $1$-norm or the $\infty$-norm, by a method which only requires $\mathit{O}\left(n^2\right)$ additional operations, assuming that a suitable factorization of $A$ is available.

The method used in this chapter is Higham's modification of Hager's method (see Higham (1988)). It yields an estimate which is never larger than the true value, but which seldom falls short by more than a factor of $3$ (although artificial examples can be constructed where it is much smaller). This is acceptable since it is the order of magnitude of $\kappa \left(A\right)$ which is important rather than its precise value.

Because $\kappa \left(A\right)$ is infinite if $A$ is singular, the functions in this chapter actually return the reciprocal of $\kappa \left(A\right)$.

The condition of a matrix and hence the accuracy of the computed solution, may be improved by scaling; thus if $D_1$ and $D_2$ are diagonal matrices with positive diagonal elements, then is the scaled matrix. A general matrix is said to be equilibrated if it is scaled so that the lengths of its rows and columns have approximately equal magnitude. Similarly a general matrix is said to be row-equilibrated (column-equilibrated) if it is scaled so that the lengths of its rows (columns) have approximately equal magnitude. Note that row scaling can affect the choice of pivot when partial pivoting is used in the factorization of $A$.

A symmetric or Hermitian positive definite matrix is said to be equilibrated if the diagonal elements are all approximately equal to unity.

For further information on scaling and equilibration see Section 3.5.2 of Golub and Van Loan (1996), Section 7.2, 7.3 and 9.8 of Higham (1988) and Section 5 of Chapter 4 of Wilkinson (1965).

Functions are provided to return the scaling factors that equilibrate a matrix for general, general band, symmetric and Hermitian positive definite and symmetric and Hermitian positive definite band matrices.

A disadvantage of normwise error bounds is that they do not reflect any special structure in the data $A$ and $b$ – that is, a pattern of elements which are known to be zero – and the bounds are dominated by the largest elements in the data.

Componentwise error bounds overcome these limitations. Instead of the normwise relative error, we can bound the relative error in each component of $A$ and $b$: where the component-wise backward error bound $\omega$ is given by

Functions are provided in this chapter which compute $\omega$, and also compute a forward error bound which is sometimes much sharper than the normwise bound given earlier:

Care is taken when computing this bound to allow for rounding errors in computing $r$. The norm ${‖\left|A^{-1}\right|.\left|r\right|‖}_{\infty }$ is estimated cheaply (without computing $A^{-1}$) by a modification of the method used to estimate $\kappa \left(A\right)$.

If $\hat{x}$ is an approximate computed solution to $Ax=b$, and $r$ is the corresponding residual, then a procedure for iterative refinement of $\hat{x}$ can be defined as follows, starting with $x_0=\hat{x}$:

• for $i=0,1,\dots$, until convergence

  compute	$r_i=b-A{x}_i$
  solve	$A{d}_i=r_i$
  compute	$x_{i+1}=x_i+d_i$

In Chapter F04, functions are provided which perform this procedure using additional precision to compute $r$, and are thus able to reduce the forward error to the level of machine precision.

The functions in this chapter do not use additional precision to compute $r$, and cannot guarantee a small forward error, but can guarantee a small backward error (except in rare cases when $A$ is very ill-conditioned, or when $A$ and $x$ are sparse in such a way that $\left|A\right|.\left|x\right|$ has a zero or very small component). The iterations continue until the backward error has been reduced as much as possible; usually only one iteration is needed.

It is seldom necessary to compute an explicit inverse of a matrix. In particular, do not attempt to solve $Ax=b$ by first computing $A^{-1}$ and then forming the matrix-vector product $x=A^{-1}b$; the procedure described in Solution of Systems of Equations is more efficient and more accurate.

However, functions are provided for the rare occasions when an inverse is needed, using one of the factorizations described in Matrix Factorizations.

Functions which handle symmetric matrices are usually designed so that they use either the upper or lower triangle of the matrix; it is not necessary to store the whole matrix. If the upper or lower triangle is stored conventionally in the upper or lower triangle of a two-dimensional array, the remaining elements of the array can be used to store other useful data.

However, that is not always convenient, and if it is important to economize on storage, the upper or lower triangle can be stored in a one-dimensional array of length $n\left(n+1\right)/2$ or a two-dimensional array with $n\left(n+1\right)/2$ elements; in other words, the storage is almost halved.

The one-dimensional array storage format is referred to as packed storage; it is described in Packed storage. The two-dimensional array storage format is referred to as Rectangular Full Packed (RFP) format; it is described in Rectangular Full Packed (RFP) Storage. They may also be used for triangular matrices.

Functions designed for these packed storage formats perform the same number of arithmetic operations as functions which use conventional storage. Those using a packed one-dimensional array are usually less efficient, especially on high-performance computers, so there is then a trade-off between storage and efficiency. The RFP functions are as efficient as for conventional storage, although only a small subset of functions use this format.

A band matrix is one whose nonzero elements are confined to a relatively small number of subdiagonals or superdiagonals on either side of the main diagonal. A tridiagonal matrix is a special case of a band matrix with just one subdiagonal and one superdiagonal. Algorithms can take advantage of bandedness to reduce the amount of work and storage required. The storage scheme used for band matrices is described in Band storage.

The $LU$ factorization for general matrices, and the Cholesky factorization for symmetric and Hermitian positive definite matrices both preserve bandedness. Hence functions are provided which take advantage of the band structure when solving systems of linear equations.

The Cholesky factorization preserves bandedness in a very precise sense: the factor $U$ or $L$ has the same number of superdiagonals or subdiagonals as the original matrix. In the $LU$ factorization, the row-interchanges modify the band structure: if $A$ has $k_l$ subdiagonals and $k_u$ superdiagonals, then $L$ is not a band matrix but still has at most $k_l$ nonzero elements below the diagonal in each column; and $U$ has at most $k_l+k_u$ superdiagonals.

The Bunch–Kaufman factorization does not preserve bandedness, because of the need for symmetric row-and-column permutations; hence no functions are provided for symmetric indefinite band matrices.

The inverse of a band matrix does not in general have a band structure, so no functions are provided for computing inverses of band matrices.

Many of the functions in this chapter use what is termed a block partitioned algorithm. This means that at each major step of the algorithm a block of rows or columns is updated, and most of the computation is performed by matrix-matrix operations on these blocks. The matrix-matrix operations are performed by calls to the Level 3 BLAS which are the key to achieving high performance on many modern computers. See Golub and Van Loan (1996) or Anderson et al. (1999) for more about block partitioned algorithms.

The performance of a block partitioned algorithm varies to some extent with the block size – that is, the number of rows or columns per block. This is a machine-dependent argument, which is set to a suitable value when the library is implemented on each range of machines. You do not normally need to be aware of what value is being used. Different block sizes may be used for different functions. Values in the range $16$ to $64$ are typical.

On some machines there may be no advantage from using a block partitioned algorithm, and then the functions use an unblocked algorithm (effectively a block size of $1$), relying solely on calls to the Level 2 BLAS again).

Some LAPACK routines use mixed precision arithmetic in an effort to solve problems more efficiently on modern hardware. They work by converting a double precision problem into an equivalent single precision problem, solving it and then using iterative refinement in double precision to find a full precision solution to the original problem. The method may fail if the problem is too ill-conditioned to allow the initial single precision solution, in which case the functions fall back to solve the original problem entirely in double precision. The vast majority of problems are not so ill-conditioned, and in those cases the technique can lead to significant gains in speed without loss of accuracy. This is particularly true on machines where double precision arithmetic is significantly slower than single precision.

Tables 1 to 8 in Tables of Driver and Computational Routines show the functions which are provided for performing different computations on different types of matrices. Tables 1 to 4 show functions for real matrices; Tables 5 to 8 show functions for complex matrices. Each entry in the table gives the NAG function name and the LAPACK double precision name.

Functions are provided for the following types of matrix:

• general
• general band
• general tridiagonal
• symmetric or Hermitian positive definite
• symmetric or Hermitian positive definite (packed storage)
• symmetric or Hermitian positive definite (RFP storage)
• symmetric or Hermitian positive definite band
• symmetric or Hermitian positive definite tridiagonal
• symmetric or Hermitian indefinite
• symmetric or Hermitian indefinite (packed storage)
• triangular
• triangular (packed storage)
• triangular (RFP storage)
• triangular band

For each of the above types of matrix (except where indicated), functions are provided to perform the following computations:

(a)	(except for RFP matrices) solve a system of linear equations (driver functions);
(b)	(except for RFP matrices) solve a system of linear equations with condition and error estimation (expert drivers);
(c)	(except for triangular matrices) factorize the matrix (see Matrix Factorizations);
(d)	solve a system of linear equations, using the factorization (see Solution of Systems of Equations);
(e)	(except for RFP matrices) estimate the condition number of the matrix, using the factorization (see Estimating condition numbers); these functions also require the norm of the original matrix (except when the matrix is triangular) which may be computed by a function in
(f)	(except for RFP matrices) refine the solution and compute forward and backward error bounds (see Componentwise error bounds and Iterative refinement of the solution); these functions require the original matrix and right-hand side, as well as the factorization returned from (a) and the solution returned from (b);
(g)	(except for band and tridiagonal matrices) invert the matrix, using the factorization (see Matrix Inversion);
(h)	(except for tridiagonal, symmetric indefinite, triangular and RFP matrices) compute scale factors to equilibrate the matrix (see Scaling and Equilibration).

Thus, to solve a particular problem, it is usually only necessary to call a single driver function, but alternatively two or more functions may be called in succession. This is illustrated in the example programs in the function documents.

In this chapter the following different storage schemes are used for matrices:

• – conventional storage in a two-dimensional array;
• – packed storage for symmetric, Hermitian or triangular matrices;
• – rectangular full packed (RFP) storage for symmetric, Hermitian or triangular matrices;
• – band storage for band matrices.

In the examples below, $*$ indicates an array element which need not be set and is not referenced by the functions. .

The default scheme for storing matrices is the obvious one: a matrix $A$ is stored in a two-dimensional array a, with matrix element $a_{ij}$ stored in array element $\mathrm{a}\left(i,j\right)$.

If a matrix is triangular (upper or lower, as specified by the argument uplo), only the elements of the relevant triangle are stored; the remaining elements of the array need not be set. Such elements are indicated by * or $⌴$ in the examples below.

For example, when $n=4$:

Functions which handle symmetric or Hermitian matrices allow for either the upper or lower triangle of the matrix (as specified by uplo) to be stored in the corresponding elements of the array; the remaining elements of the array need not be set.

For example, when $n=4$:

Symmetric, Hermitian or triangular matrices may be stored more compactly, if the relevant triangle (again as specified by uplo) is packed by columns in a one-dimensional array. In this chapter, as in Chapter F08, arrays which hold matrices in packed storage, have names ending in P. For a matrix of order $n$, the array must have at least $n\left(n+1\right)/2$ elements. So:

• if $\mathrm{uplo}=\text{'U'}$, $a_{ij}$ is stored in $\mathrm{ap}\left(i+j\left(j-1\right)/2\right)$ for $i\le j$;
• if $\mathrm{uplo}=\text{'L'}$, $a_{ij}$ is stored in $\mathrm{ap}\left(i+\left(2n-j\right)\left(j-1\right)/2\right)$ for $j\le i$.

For example:

Note that for real symmetric matrices, packing the upper triangle by columns is equivalent to packing the lower triangle by rows; packing the lower triangle by columns is equivalent to packing the upper triangle by rows. (For complex Hermitian matrices, the only difference is that the off-diagonal elements are conjugated.)

The rectangular full packed (RFP) storage format offers the same savings in storage as the packed storage format (described in Packed storage), but is likely to be much more efficient in general since the block structure of the matrix is maintained. This structure can be exploited using block partition algorithms (see Block Partitioned Algorithms) in a similar way to matrices that use conventional storage.

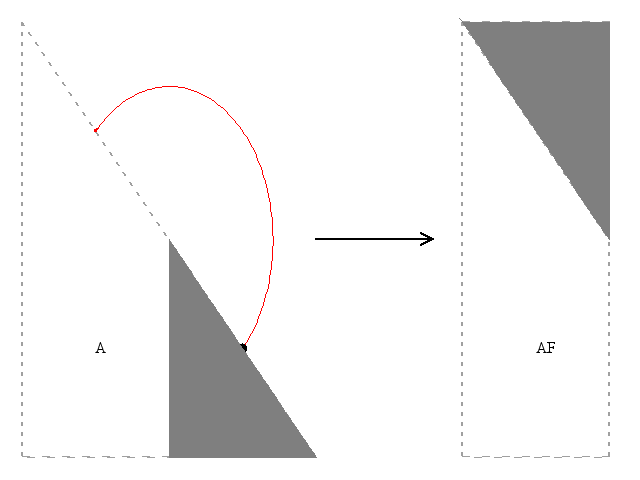
Figure 1 gives a graphical representation of the key idea of RFP for the particular case of a lower triangular matrix of even dimensions. In all cases the original triangular matrix of stored elements is separated into a trapezoidal part and a triangular part. The number of columns in these two parts is equal when the dimension of the matrix is even, $n=2k$, while the trapezoidal part has $k+1$ columns when $n=2k+1$. The smaller part is then transposed and fitted onto the trapezoidal part forming a rectangle. The rectangle has dimensions $2k+1$ and $q$, where $q=k$ when $n$ is even and $q=k+1$ when $n$ is odd.

For functions using RFP there is the option of storing the rectangle as described above ($\mathrm{transr}=\text{'N'}$) or its transpose ($\mathrm{transr}=\text{'T'}$, for real a) or its conjugate transpose ($\mathrm{transr}=\text{'C'}$, for complex a).

As an example, we first consider RFP for the case $n=2k$ with $k=3$.

If $\mathrm{transr}=\text{'N'}$, then ar holds a as follows:

• For $\mathrm{uplo}=\text{'U'}$ the upper trapezoid $\mathrm{ar}\left(1:6,1:3\right)$ consists of the last three columns of a upper. The lower triangle $\mathrm{ar}\left(5:7,1:3\right)$ consists of the transpose of the first three columns of a upper.
• For $\mathrm{uplo}=\text{'L'}$ the lower trapezoid $\mathrm{ar}\left(2:7,1:3\right)$ consists of the first three columns of a lower. The upper triangle $\mathrm{ar}\left(1:3,1:3\right)$ consists of the transpose of the last three columns of a lower.

If $\mathrm{transr}=\text{'T'}$, then ar in both uplo cases is just the transpose of ar as defined when $\mathrm{transr}=\text{'N'}$.

Now we consider RFP for the case $n=2k+1$ and $k=2$.

If $\mathrm{transr}=\text{'N'}$. ar holds a as follows:

• if $\mathrm{uplo}=\text{'U'}$ the upper trapezoid $\mathrm{ar}\left(1:5,1:3\right)$ consists of the last three columns of a upper. The lower triangle $\mathrm{ar}\left(4:5,1:2\right)$ consists of the transpose of the first two columns of a upper;
• if $\mathrm{uplo}=\text{'L'}$ the lower trapezoid $\mathrm{ar}\left(1:5,1:3\right)$ consists of the first three columns of a lower. The upper triangle $\mathrm{ar}\left(1:2,2:3\right)$ consists of the transpose of the last two columns of a lower.

If $\mathrm{transr}=\text{'T'}$. ar in both uplo cases is just the transpose of ar as defined when $\mathrm{transr}=\text{'N'}$.

Explicitly, in the real matrix case, ar is a one-dimensional array of length $n\left(n+1\right)/2$ and contains the elements of a as follows:

for $\mathrm{uplo}=\text{'U'}$ and $\mathrm{transr}=\text{'N'}$,

$a_{ij}$ is stored in $\mathrm{ar}\left(\left(2k+1\right)\left(\mathit{i}-1\right)+\mathit{j}+k+1\right)$, for $1\le \mathit{j}\le k$ and $1\le i\le \mathit{j}$, and
$a_{ij}$ is stored in $\mathrm{ar}\left(\left(2k+1\right)\left(\mathit{j}-k-1\right)+i\right)$, for $k<j\le n$ and $1\le i\le j$;

for $\mathrm{uplo}=\text{'U'}$ and $\mathrm{transr}=\text{'T'}$,

$a_{ij}$ is stored in $\mathrm{ar}\left(q\left(j+k\right)+i\right)$, for $1\le j\le k$ and $1\le i\le j$, and
$a_{ij}$ is stored in $\mathrm{ar}\left(q\left(i-1\right)+\mathit{j}-k\right)$, for $k<j\le n$ and $1\le i\le j$;

for $\mathrm{uplo}=\text{'L'}$ and $\mathrm{transr}=\text{'N'}$,

$a_{ij}$ is stored in $\mathrm{ar}\left(\left(2k+1\right)\left(j-1\right)+i+k-q+1\right)$, for $1\le j\le q$ and $j\le i\le n$, and
$a_{ij}$ is stored in $\mathrm{ar}\left(\left(2k+1\right)\left(i-k-1\right)+j-q\right)$, for $q<j\le n$ and $j\le i\le n$;

for $\mathrm{uplo}=\text{'L'}$ and $\mathrm{transr}=\text{'T'}$,

$a_{ij}$ is stored in $\mathrm{ar}\left(q\left(i+k-q\right)+j\right)$, for $1\le j\le q$ and $1\le i\le n$, and
$a_{ij}$ is stored in $\mathrm{ar}\left(q\left(j-1-q\right)+i-k\right)$, for $q<j\le n$ and $1\le i\le n$.

In the case of complex matrices, the assumption is that the full matrix, if it existed, would be Hermitian. Thus, when $\mathrm{transr}=\text{'N'}$, the triangular portion of a that is, in the real case, transposed into the notional $\left(2k+1\right)$ by $q$ RFP matrix is also conjugated. When $\mathrm{transr}=\text{'C'}$ the notional $q$ by $\left(2k+1\right)$ RFP matrix is the conjugate transpose of the corresponding $\mathrm{transr}=\text{'N'}$ RFP matrix. Explicitly, for complex a, the array ar contains the elements (or conjugated elements) of a as follows:

for $\mathrm{uplo}=\text{'U'}$ and $\mathrm{transr}=\text{'N'}$,

${\stackrel{-}{a}}_{ij}$ is stored in $\mathrm{ar}\left(\left(2k+1\right)\left(\mathit{i}-1\right)+\mathit{j}+k+1\right)$, for $1\le \mathit{j}\le k$ and $1\le i\le \mathit{j}$, and
$a_{ij}$ is stored in $\mathrm{ar}\left(\left(2k+1\right)\left(\mathit{j}-k-1\right)+i\right)$, for $k<j\le n$ and $1\le i\le j$;

for $\mathrm{uplo}=\text{'U'}$ and $\mathrm{transr}=\text{'C'}$,

$a_{ij}$ is stored in $\mathrm{ar}\left(q\left(j+k\right)+i\right)$, for $1\le j\le k$ and $1\le i\le j$, and
${\stackrel{-}{a}}_{ij}$ is stored in $\mathrm{ar}\left(q\left(i-1\right)+\mathit{j}-k\right)$, for $k<j\le n$ and $1\le i\le j$;

for $\mathrm{uplo}=\text{'L'}$ and $\mathrm{transr}=\text{'N'}$,

$a_{ij}$ is stored in $\mathrm{ar}\left(\left(2k+1\right)\left(j-1\right)+i+k-q+1\right)$, for $1\le j\le q$ and $j\le i\le n$, and
${\stackrel{-}{a}}_{ij}$ is stored in $\mathrm{ar}\left(\left(2k+1\right)\left(i-k-1\right)+j-q\right)$, for $q<j\le n$ and $j\le i\le n$;

for $\mathrm{uplo}=\text{'L'}$ and $\mathrm{transr}=\text{'C'}$,

${\stackrel{-}{a}}_{ij}$ is stored in $\mathrm{ar}\left(q\left(i+k-q\right)+j\right)$, for $1\le j\le q$ and $1\le i\le n$, and
$a_{ij}$ is stored in $\mathrm{ar}\left(q\left(j-1-q\right)+i-k\right)$, for $q<j\le n$ and $1\le i\le n$.

A band matrix with $k_l$ subdiagonals and $k_u$ superdiagonals may be stored compactly in a two-dimensional array with $k_l+k_u+1$ rows and $n$ columns. Columns of the matrix are stored in corresponding columns of the array, and diagonals of the matrix are stored in rows of the array. This storage scheme should be used in practice only if $k_l$, $k_u\ll n$, although the functions in Chapters F07 and F08 work correctly for all values of $k_l$ and $k_u$. In Chapters F07 and F08 arrays which hold matrices in band storage have names ending in $\mathrm{B}$.

To be precise, elements of matrix elements $a_{ij}$ are stored as follows:

• $a_{ij}$ is stored in $\mathrm{ab}\left(k_u+1+i-j,j\right)$ for $\max \left(1,j-k_u\right)\le i\le \min \left(n,j+k_l\right)$.

For example, when $n=5$, $k_l=2$ and $k_u=1$:

The elements marked $*$ in the upper left and lower right corners of the array ab need not be set, and are not referenced by the functions.

Note:  when a general band matrix is supplied for $LU$ factorization, space must be allowed to store an additional $k_l$ superdiagonals, generated by fill-in as a result of row interchanges. This means that the matrix is stored according to the above scheme, but with $k_l+k_u$ superdiagonals.

Triangular band matrices are stored in the same format, with either $k_l=0$ if upper triangular, or $k_u=0$ if lower triangular.

For symmetric or Hermitian band matrices with $k$ subdiagonals or superdiagonals, only the upper or lower triangle (as specified by uplo) need be stored:

• if $\mathrm{uplo}=\text{'U'}$, $a_{ij}$ is stored in $\mathrm{ab}\left(k+1+i-j,j\right)$ for $\max \left(1,j-k\right)\le i\le j$;
• if $\mathrm{uplo}=\text{'L'}$, $a_{ij}$ is stored in $\mathrm{ab}\left(1+i-j,j\right)$ for $j\le i\le \min \left(n,j+k\right)$.

For example, when $n=5$ and $k=2$:

Note that different storage schemes for band matrices are used by some functions in Chapters F01, F02, F03 and F04.

Some functions in this chapter have an option to handle unit triangular matrices (that is, triangular matrices with diagonal elements $=1$). This option is specified by a argument diag. If $\mathrm{diag}=\text{'U'}$ (Unit triangular), the diagonal elements of the matrix need not be stored, and the corresponding array elements are not referenced by the functions. The storage scheme for the rest of the matrix (whether conventional, packed or band) remains unchanged.

Complex Hermitian matrices have diagonal elements that are by definition purely real. In addition, complex triangular matrices which arise in Cholesky factorization are defined by the algorithm to have real diagonal elements.

If such matrices are supplied as input to functions in Chapters F07 and F08, the imaginary parts of the diagonal elements are not referenced, but are assumed to be zero. If such matrices are returned as output by the functions, the computed imaginary parts are explicitly set to zero.

Most functions in this chapter have one or more option arguments, of type string. The descriptions in Section 5 of the function documents refer only to upper-case values (for example $\mathrm{uplo}=\text{'U'}$ or $\text{'L'}$); however, in every case, the corresponding lower-case characters may be supplied (with the same meaning). Any other value is illegal.

A longer character string can be passed as the actual argument, making the calling program more readable, but only the first character is significant. For example:

[b, info] = f07ae('Transpose', a, ipiv, b);

It is permissible for the problem dimensions (for example, m in nag_lapack_dgetrf (f07ad), n or nrhs_p in nag_lapack_dgetrs (f07ae)) to be passed as zero, in which case the computation (or part of it) is skipped. Negative dimensions are regarded as an error.