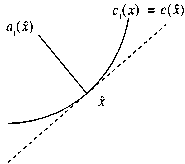E04 Chapter Introduction:: Minimizing or Maximizing a Function (NAG Toolbox)

An optimization problem involves minimizing a function (called the objective function) of several variables, possibly subject to restrictions on the values of the variables defined by a set of constraint functions. Most functions in the Library are concerned with function minimization only, since the problem of maximizing a given objective function F(x) is equivalent to minimizing

- F (x)

. Some functions allow you to specify whether you are solving a minimization or maximization problem, carrying out the required transformation of the objective function in the latter case.

In general functions in this chapter find a local minimum of a function

f

, that is a point

x^{*}

s.t. for all

x

near

x^{*} f (x) \geq f (x^{*})

.

Chapter E05 contains functions to find the global minimum of a function

f

. At a global minimum

x^{*} f (x) \geq f (x^{*})

for all

x

.

Chapter H contains functions typically regarded as belonging to the field of operations research.

This introduction is only a brief guide to the subject of optimization designed for the casual user. Anyone with a difficult or protracted problem to solve will find it beneficial to consult a more detailed text, see Gill et al. (1981) or Fletcher (1987). If you are unfamiliar with the mathematics of the subject you may find the more detailed text difficult at first reading; if so, you should concentrate on Types of Optimization Problems, Geometric Representation and Terminology, Scaling, Analysis of Computed Results and Recommendations on Choice and Use of Available Functions.

The solution of optimization problems by a single, all-purpose, method is cumbersome and inefficient. Optimization problems are therefore classified into particular categories, where each category is defined by the properties of the objective and constraint functions, as illustrated by some examples below.

Properties of Objective Function	Properties of Constraints
Nonlinear	Nonlinear
Sums of squares of nonlinear functions	Sparse linear
Quadratic	Linear
Sums of squares of linear functions	Bounds
Linear	None

For instance, a specific problem category involves the minimization of a nonlinear objective function subject to bounds on the variables. In the following sections we define the particular categories of problems that can be solved by functions contained in this chapter. Not every category is given special treatment in the current version of the Library; however, the long-term objective is to provide a comprehensive set of functions to solve problems in all such categories.

In unconstrained minimization problems there are no constraints on the variables. The problem can be stated mathematically as follows:

\underset{x}{minimize} F (x)

where

x \in R^{n}

, that is,

x = {(x_{1}, x_{2}, \dots, x_{n})}^{T}

.

Special consideration is given to the problem for which the function to be minimized can be expressed as a sum of squared functions. The least squares problem can be stated mathematically as follows:

\underset{x}{minimize} \{f^{T} f = \sum_{i = 1}^{m} f_{i}^{2} (x)\}, x \in R^{n}

where the

i

th element of the

m

-vector

f

is the function

f_{i} (x)

.

These problems differ from the unconstrained problem in that at least one of the variables is subject to a simple bound (or restriction) on its value, e.g.,

x_{5} \leq 10

, but no constraints of a more general form are present.

The problem can be stated mathematically as follows:

\underset{x}{minimize} F (x), x \in R^{n}

subject to

l_{i} \leq x_{i} \leq u_{i}

, for

i = 1, 2, \dots, n

.

This format assumes that upper and lower bounds exist on all the variables. By conceptually allowing

u_{i} = + \infty

and

l_{i} = - \infty

all the variables need not be restricted.

A general linear constraint is defined as a constraint function that is linear in more than one of the variables, e.g.,

3 x_{1} + 2 x_{2} \geq 4

. The various types of linear constraint are reflected in the following mathematical statement of the problem:

\underset{x}{minimize} F (x), x \in R^{n}

subject to the

equality constraints:	$a_{i}^{T} x = b_{i}$	$i = 1, 2, \dots, m_{1}$ ;
inequality constraints:	$a_{i}^{T} x \geq b_{i}$	$i = m_{1} + 1, m_{1} + 2, \dots, m_{2}$ ;
	$a_{i}^{T} x \leq b_{i}$	$i = m_{2} + 1, m_{2} + 2, \dots, m_{3}$ ;
range constraints:	$s_{j} \leq a_{i}^{T} x \leq t_{j}$	$i = m_{3} + 1, m_{3} + 2, \dots, m_{4};$
		$j = 1, 2, \dots, m_{4} - m_{3};$
bounds constraints:	$l_{i} \leq x_{i} \leq u_{i}$	$i = 1, 2, \dots, n$

where each

a_{i}

is a vector of length

n

;

b_{i}

,

s_{j}

and

t_{j}

are constant scalars; and any of the categories may be empty.

Although the bounds on

x_{i}

could be included in the definition of general linear constraints, we prefer to distinguish between them for reasons of computational efficiency.

If

F (x)

is a linear function, the linearly-constrained problem is termed a linear programming problem (LP); if

F (x)

is a quadratic function, the problem is termed a quadratic programming problem (QP). For further discussion of LP and QP problems, including the dual formulation of such problems, see Dantzig (1963).

A problem is included in this category if at least one constraint function is nonlinear, e.g.,

x_{1}^{2} + x_{3} + x_{4} - 2 \geq 0

. The mathematical statement of the problem is identical to that for the linearly-constrained case, except for the addition of the following constraints:

equality constraints:	$c_{i} (x) = 0$	$i = 1, 2, \dots, m_{5}$ ;
inequality constraints:	$c_{i} (x) \geq 0$	$i = m_{5} + 1, m_{5} + 2, \dots, m_{6}$ ;
range constraints:	$v_{j} \leq c_{i} (x) \leq w_{j}$	$i = m_{6} + 1, m_{6} + 2, \dots, m_{7}$ ,
		$j = 1, 2, \dots, m_{7} - m_{6}$

where each

c_{i}

is a nonlinear function;

v_{j}

and

w_{j}

are constant scalars; and any category may be empty. Note that we do not include a separate category for constraints of the form

c_{i} (x) \leq 0

, since this is equivalent to

- c_{i} (x) \geq 0

.

Although the general linear constraints could be included in the definition of nonlinear constraints, again we prefer to distinguish between them for reasons of computational efficiency.

If

F (x)

is a nonlinear function, the nonlinearly-constrained problem is termed a nonlinear programming problem (NLP). For further discussion of NLP problems, see Gill et al. (1981) or Fletcher (1987).

In all of the above problem categories it is assumed that

a \leq F (x) \leq b

where

a = - \infty

and

b = + \infty

. Problems in which

a

and/or

b

are finite can be solved by adding an extra constraint of the appropriate type (i.e., linear or nonlinear) depending on the form of

F (x)

. Further advice is given in Function Evaluations at Infeasible Points.

Sometimes a problem may have two or more objective functions which are to be optimized at the same time. Such problems are called multi-object, multi-criteria or multi-attribute optimization. If the constraints are linear and the objectives are all linear then the terminology ‘goal programming’ is also used.

Techniques used in this chapter and in Chapter E05 may be employed to address such problems.

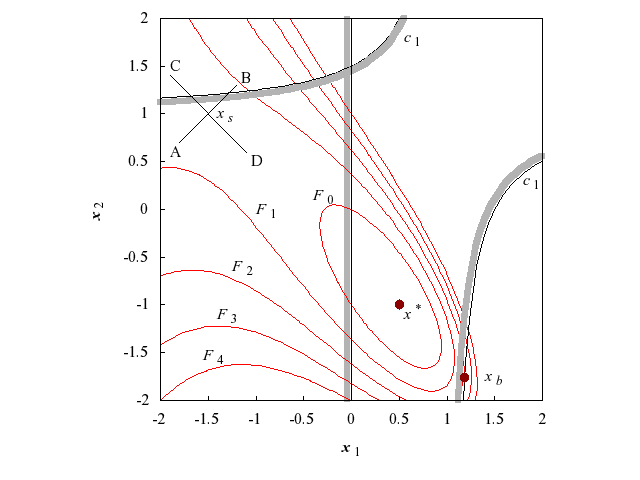
To illustrate the nature of optimization problems it is useful to consider the following example in two dimensions:

F (x) = e^{x_{1}} (4 x_{1}^{2} + 2 x_{2}^{2} + 4 x_{1} x_{2} + 2 x_{2} + 1) .

(This function is used as the example function in the documentation for the unconstrained functions.)

Figure 1

Figure 1 is a contour diagram of

F (x)

. The contours labelled

F_{0}, F_{1}, \dots, F_{4}

are isovalue contours, or lines along which the function

F (x)

takes specific constant values. The point

x^{*} = {(\frac{1}{2}, - 1)}^{T}

is a local unconstrained minimum, that is, the value of

F (x^{*})

(

= 0

) is less than at all the neighbouring points. A function may have several such minima. The lowest of the local minima is termed a global minimum. In the problem illustrated in Figure 1,

x^{*}

is the only local minimum. The point

x_{s}

is said to be a saddle point because it is a minimum along the line AB, but a maximum along CD.

If we add the constraint

x_{1} \geq 0

(a simple bound) to the problem of minimizing

F (x)

, the solution remains unaltered. In Figure 1 this constraint is represented by the straight line passing through

x_{1} = 0

, and the shading on the line indicates the unacceptable region (i.e.,

x_{1} < 0

). The region in

R^{n}

satisfying the constraints of an optimization problem is termed the feasible region. A point satisfying the constraints is defined as a feasible point.

If we add the nonlinear constraint

c_{1} (x) : x_{1} + x_{2} - x_{1} x_{2} - \frac{3}{2} \geq 0

, represented by the curved shaded line in Figure 1, then

x^{*}

is not a feasible point because

c_{1} (x^{*}) < 0

. The solution of the new constrained problem is

x_{b} ≃ {(1.1825, - 1.7397)}^{T}

, the feasible point with the smallest function value (where

F (x_{b}) ≃ 3.0607

).

The vector of first partial derivatives of

F (x)

is called the gradient vector, and is denoted by

g (x)

, i.e.,

g (x) = {[\frac{\partial F (x)}{\partial x_{1}}, \frac{\partial F (x)}{\partial x_{2}}, \dots, \frac{\partial F (x)}{\partial x_{n}}]}^{T} .

For the function illustrated in Figure 1,

g (x) = [\begin{matrix} F (x) + e^{x_{1}} (8 x_{1} + 4 x_{2}) \\ e^{x_{1}} (4 x_{2} + 4 x_{1} + 2) \end{matrix}] .

The gradient vector is of importance in optimization because it must be zero at an unconstrained minimum of any function with continuous first derivatives.

The matrix of second partial derivatives of a function is termed its Hessian matrix. The Hessian matrix of

F (x)

is denoted by

G (x)

, and its

(i, j)

th element is given by

\partial^{2} F (x) / \partial x_{i} \partial x_{j}

. If

F (x)

has continuous second derivatives, then

G (x)

must be positive definite at any unconstrained minimum of

F

.

In nonlinear least squares problems, the matrix of first partial derivatives of the vector-valued function

f (x)

is termed the Jacobian matrix of

f (x)

and its

(i, j)

th component is

\partial f_{i} / \partial x_{j}

.

The vector of first partial derivatives of the constraint

c_{i} (x)

is denoted by

a_{i} (x) = {[\frac{\partial c_{i} (x)}{\partial x_{1}}, \frac{\partial c_{i} (x)}{\partial x_{2}}, \dots, \frac{\partial c_{i} (x)}{\partial x_{n}}]}^{T} .

The matrix whose columns are the vectors

\{a_{i}\}

is termed the matrix of constraint normals. At a point

\hat{x}

, the vector

a_{i} (\hat{x})

is orthogonal (normal) to the isovalue contour of

c_{i} (x)

passing through

\hat{x}

; this relationship is illustrated for a two-dimensional function in Figure 2.

Figure 2

Note that if

c_{i} (x)

is a linear constraint involving

a_{i}^{T} x

, then its vector of first partial derivatives is simply the vector

a_{i}

.

All nonlinear functions will be assumed to have continuous second derivatives in the neighbourhood of the solution.

The following conditions are sufficient for the point

x^{*}

to be an unconstrained local minimum of

F (x)

:

(i)	$‖g (x^{*})‖ = 0$ ; and
(ii)	$G (x^{*})$ is positive definite,

where

‖g‖

denotes the Euclidean length of

g

At the solution of a bounds-constrained problem, variables which are not on their bounds are termed free variables. If it is known in advance which variables are on their bounds at the solution, the problem can be solved as an unconstrained problem in just the free variables; thus, the sufficient conditions for a solution are similar to those for the unconstrained case, applied only to the free variables.

Sufficient conditions for a feasible point

x^{*}

to be the solution of a bounds-constrained problem are as follows:

(i)	$‖\bar{g} (x^{*})‖ = 0$ ; and
(ii)	$\bar{G} (x^{*})$ is positive definite; and
(iii)	$g_{j} (x^{}) < 0, x_{j} = u_{j}$ ; $g_{j} (x^{}) > 0, x_{j} = l_{j}$ ,

where

\bar{g} (x)

is the gradient of

F (x)

with respect to the free variables, and

\bar{G} (x)

is the Hessian matrix of

F (x)

with respect to the free variables. The extra condition (iii) ensures that

F (x)

cannot be reduced by moving off one or more of the bounds.

For the sake of simplicity, the following description does not include a specific treatment of bounds or range constraints, since the results for general linear inequality constraints can be applied directly to these cases.

At a solution

x^{*}

, of a linearly-constrained problem, the constraints which hold as equalities are called the active or binding constraints. Assume that there are

t

active constraints at the solution

x^{*}

, and let

\hat{A}

denote the matrix whose columns are the columns of

A

corresponding to the active constraints, with

\hat{b}

the vector similarly obtained from

b

; then

{\hat{A}}^{T} x^{*} = \hat{b} .

The matrix

Z

is defined as an

n \times (n - t)

matrix satisfying:

\begin{array}{l} {\hat{A}}^{T} Z = 0; \\ Z^{T} Z = I . \end{array}

The columns of

Z

form an orthogonal basis for the set of vectors orthogonal to the columns of

\hat{A}

.

Define

$g_{Z} (x) = Z^{T} g (x)$ , the projected gradient vector of $F (x)$ ;
$G_{Z} (x) = Z^{T} G (x) Z$ , the projected Hessian matrix of $F (x)$ .

At the solution of a linearly-constrained problem, the projected gradient vector must be zero, which implies that the gradient vector

g (x^{*})

can be written as a linear combination of the columns of

\hat{A}

, i.e.,

g (x^{*}) = \sum_{i = 1}^{t} λ_{i}^{*} {\hat{a}}_{i} = \hat{A} λ^{*}

. The scalar

λ_{i}^{*}

is defined as the Lagrange multiplier corresponding to the

i

th active constraint. A simple interpretation of the

i

th Lagrange multiplier is that it gives the gradient of

F (x)

along the

i

th active constraint normal; a convenient definition of the Lagrange multiplier vector (although not a recommended method for computation) is:

λ^{*} = {({\hat{A}}^{T} \hat{A})}^{- 1} {\hat{A}}^{T} g (x^{*}) .

Sufficient conditions for

x^{*}

to be the solution of a linearly-constrained problem are:

(i)	$x^{}$ is feasible, and ${\hat{A}}^{T} x^{} = \hat{b}$ ; and
(ii)	$‖g_{Z} (x^{})‖ = 0$ , or equivalently, $g (x^{}) = \hat{A} λ^{*}$ ; and
(iii)	$G_{Z} (x^{*})$ is positive definite; and
(iv)	$λ_{i}^{} > 0$ if $λ_{i}^{}$ corresponds to a constraint ${\hat{a}}_{i}^{T} x^{} \geq {\hat{b}}_{i}$ ; $λ_{i}^{} < 0$ if $λ_{i}^{}$ corresponds to a constraint ${\hat{a}}_{i}^{T} x^{} \leq {\hat{b}}_{i}$ . The sign of $λ_{i}^{*}$ is immaterial for equality constraints, which by definition are always active.

For nonlinearly-constrained problems, much of the terminology is defined exactly as in the linearly-constrained case. The set of active constraints at

x

again means the set of constraints that hold as equalities at

x

, with corresponding definitions of

\hat{c}

and

\hat{A}

: the vector

\hat{c} (x)

contains the active constraint functions, and the columns of

\hat{A} (x)

are the gradient vectors of the active constraints. As before,

Z

is defined in terms of

\hat{A} (x)

as a matrix such that:

\begin{array}{l} {\hat{A}}^{T} Z = 0; \\ Z^{T} Z = I \end{array}

where the dependence on

x

has been suppressed for compactness.

The projected gradient vector

g_{Z} (x)

is the vector

Z^{T} g (x)

. At the solution

x^{*}

of a nonlinearly-constrained problem, the projected gradient must be zero, which implies the existence of Lagrange multipliers corresponding to the active constraints, i.e.,

g (x^{*}) = \hat{A} (x^{*}) λ^{*}

.

The Lagrangian function is given by:

L (x, λ) = F (x) - λ^{T} \hat{c} (x) .

We define

g_{L} (x)

as the gradient of the Lagrangian function;

G_{L} (x)

as its Hessian matrix, and

{\hat{G}}_{L} (x)

as its projected Hessian matrix, i.e.,

{\hat{G}}_{L} = Z^{T} G_{L} Z

.

Sufficient conditions for

x^{*}

to be the solution of a nonlinearly-constrained problem are:

(i)	$x^{}$ is feasible, and $\hat{c} (x^{}) = 0$ ; and
(ii)	$‖g_{Z} (x^{})‖ = 0$ , or, equivalently, $g (x^{}) = \hat{A} (x^{}) λ^{}$ ; and
(iii)	${\hat{G}}_{L} (x^{*})$ is positive definite; and
(iv)	$λ_{i}^{} > 0$ if $λ_{i}^{}$ corresponds to a constraint of the form ${\hat{c}}_{i} \geq 0$ . The sign of $λ_{i}^{*}$ is immaterial for equality constraints, which by definition are always active.

Note that condition (ii) implies that the projected gradient of the Lagrangian function must also be zero at

x^{*}

, since the application of

Z^{T}

annihilates the matrix

\hat{A} (x^{*})

.

All the algorithms contained in this chapter generate an iterative sequence

\{x^{(k)}\}

that converges to the solution

x^{*}

in the limit, except for some special problem categories (i.e., linear and quadratic programming). To terminate computation of the sequence, a convergence test is performed to determine whether the current estimate of the solution is an adequate approximation. The convergence tests are discussed in Analysis of Computed Results.

Most of the methods construct a sequence

\{x^{(k)}\}

satisfying:

x^{(k + 1)} = x^{(k)} + α^{(k)} p^{(k)},

where the vector

p^{(k)}

is termed the direction of search, and

α^{(k)}

is the steplength. The steplength

α^{(k)}

is chosen so that

F (x^{(k + 1)}) < F (x^{(k)})

and is computed using one of the techniques for one-dimensional optimization referred to in One-dimensional optimization.

The Library contains two special functions for minimizing a function of a single variable. Both functions are based on safeguarded polynomial approximation. One function requires function evaluations only and fits a quadratic polynomial whilst the other requires function and gradient evaluations and fits a cubic polynomial. See Section 4.1 of Gill et al. (1981).

The distinctions among methods arise primarily from the need to use varying levels of information about derivatives of

F (x)

in defining the search direction. We describe three basic approaches to unconstrained problems, which may be extended to other problem categories. Since a full description of the methods would fill several volumes, the discussion here can do little more than allude to the processes involved, and direct you to other sources for a full explanation.

(a)	Newton-type Methods (Modified Newton Methods) Newton-type methods use the Hessian matrix $G (x^{(k)})$ , or a finite difference approximation to $G (x^{(k)})$ , to define the search direction. The functions in the Library either require a function that computes the elements of $G (x^{(k)})$ directly, or they approximate $G (x^{(k)})$ by finite differences. Newton-type methods are the most powerful methods available for general problems and will find the minimum of a quadratic function in one iteration. See Sections 4.4 and 4.5.1 of Gill et al. (1981).
(b)	Quasi-Newton Methods Quasi-Newton methods approximate the Hessian $G (x^{(k)})$ by a matrix $B^{(k)}$ which is modified at each iteration to include information obtained about the curvature of $F$ along the current search direction $p^{(k)}$ . Although not as robust as Newton-type methods, quasi-Newton methods can be more efficient because $G (x^{(k)})$ is not computed directly, or approximated by finite differences. Quasi-Newton methods minimize a quadratic function in $n$ iterations, where $n$ is the number of variables. See Section 4.5.2 of Gill et al. (1981).
(c)	Conjugate-gradient Methods Unlike Newton-type and quasi-Newton methods, conjugate-gradient methods do not require the storage of an $n$ by $n$ matrix and so are ideally suited to solve large problems. Conjugate-gradient type methods are not usually as reliable or efficient as Newton-type, or quasi-Newton methods. See Section 4.8.3 of Gill et al. (1981).

These methods are similar to those for unconstrained optimization, but exploit the special structure of the Hessian matrix to give improved computational efficiency.

Since

F (x) = \sum_{i = 1}^{m} f_{i}^{2} (x)

the Hessian matrix

G (x)

is of the form

G (x) = 2 (J {(x)}^{T} J (x) + \sum_{i = 1}^{m} f_{i} (x) G_{i} (x)),

where

J (x)

is the Jacobian matrix of

f (x)

, and

G_{i} (x)

is the Hessian matrix of

f_{i} (x)

.

In the neighbourhood of the solution,

‖f (x)‖

is often small compared to

‖J {(x)}^{T} J (x)‖

(for example, when

f (x)

represents the goodness-of-fit of a nonlinear model to observed data). In such cases,

2 J {(x)}^{T} J (x)

may be an adequate approximation to

G (x)

, thereby avoiding the need to compute or approximate second derivatives of

\{f_{i} (x)\}

. See Section 4.7 of Gill et al. (1981).

Bounds on the variables are dealt with by fixing some of the variables on their bounds and adjusting the remaining free variables to minimize the function. By examining estimates of the Lagrange multipliers it is possible to adjust the set of variables fixed on their bounds so that eventually the bounds active at the solution should be correctly identified. This type of method is called an active set method. One feature of such methods is that, given an initial feasible point, all approximations

x^{(k)}

are feasible. This approach can be extended to general linear constraints. At a point,

x

, the set of constraints which hold as equalities being used to predict, or approximate, the set of active constraints is called the working set.

Nonlinear constraints are more difficult to handle. If at all possible, it is usually beneficial to avoid including nonlinear constraints during the formulation of the problem. The methods currently implemented in the Library handle nonlinearly constrained problems by transforming them into a sequence of quadratic programming problems. A feature of such methods is that

x^{(k)}

is not guaranteed to be feasible except in the limit, and this is certainly true of the functions currently in the Library. See Chapter 6, particularly Sections 6.4 and 6.5, of Gill et al. (1981).

Anyone interested in a detailed description of methods for optimization should consult the references.

Suppose we have objective functions

f_{i} (x)

,

i > 1

, all of which we need to minimize at the same time. There are two main approaches to this problem:

(a)

Combine the individual objectives into one composite objective. Typically this might be a weighted sum of the objectives, e.g.,

w_{1} f_{1} (x) + w_{2} f_{2} (x) + \dots + w_{n} f_{n} (x)

Here you choose the weights to express the relative importance of the corresponding objective. Ideally each of the

f_{i} (x)

should be of comparable size at a solution.

(b)

Order the objectives in order of importance. Suppose

f_{i}

are ordered such that

f_{i} (x)

is more important than

f_{i + 1} (x)

, for

i = 1, 2, \dots, n - 1

. Then in the lexicographical approach to multi-objective optimization a sequence of subproblems are solved. Firstly solve the problem for objective function

f_{1} (x)

and denote by

r_{1}

the value of this minimum. If

(i - 1)

subproblems have been solved with results

r_{i - 1}

then subproblem

i

becomes

\min (f_{i} (x))

subject to

r_{k} \leq f_{k} (x) \leq r_{k}

, for

k = 1, 2, \dots, i - 1

plus the other constraints.

Clearly the bounds on

f_{k}

might be relaxed at your discretion.

In general, if NAG functions from the Chapter E04 are used then only local minima are found. This means that a better solution to an individual objective might be found without worsening the optimal solutions to the other objectives. Ideally you seek a Pareto solution; one in which an improvement in one objective can only be achieved by a worsening of another objective.

To obtain a Pareto solution functions from Chapter E05 might be used or, alternatively, a pragmatic attempt to derive a global minimum might be tried (see nag_glopt_nlp_multistart_sqp (e05uc)). In this approach a variety of different minima are computed for each subproblem by starting from a range of different starting points. The best solution achieved is taken to be the global minimum. The more starting points chosen the greater confidence you might have in the computed global minimum.

Scaling (in a broadly defined sense) often has a significant influence on the performance of optimization methods. Since convergence tolerances and other criteria are necessarily based on an implicit definition of ‘small’ and ‘large’, problems with unusual or unbalanced scaling may cause difficulties for some algorithms. Although there are currently no user-callable scaling functions in the Library, scaling is automatically performed by default in the functions which solve sparse LP, QP or NLP problems and in some newer dense solver functions. The following sections present some general comments on problem scaling.

One method of scaling is to transform the variables from their original representation, which may reflect the physical nature of the problem, to variables that have certain desirable properties in terms of optimization. It is generally helpful for the following conditions to be satisfied:

(i)	the variables are all of similar magnitude in the region of interest;
(ii)	a fixed change in any of the variables results in similar changes in $F (x)$ . Ideally, a unit change in any variable produces a unit change in $F (x)$ ;
(iii)	the variables are transformed so as to avoid cancellation error in the evaluation of $F (x)$ .

Normally, you should restrict yourself to linear transformations of variables, although occasionally nonlinear transformations are possible. The most common such transformation (and often the most appropriate) is of the form

x_{new} = D x_{old},

where

D

is a diagonal matrix with constant coefficients. Our experience suggests that more use should be made of the transformation

x_{new} = D x_{old} + v,

where

v

is a constant vector.

Consider, for example, a problem in which the variable

x_{3}

represents the position of the peak of a Gaussian curve to be fitted to data for which the extreme values are

150

and

170

; therefore

x_{3}

is known to lie in the range

150

–

170

. One possible scaling would be to define a new variable

{\bar{x}}_{3}

, given by

{\bar{x}}_{3} = \frac{x_{3}}{170} .

A better transformation, however, is given by defining

{\bar{x}}_{3}

as

{\bar{x}}_{3} = \frac{x_{3} - 160}{10} .

Frequently, an improvement in the accuracy of evaluation of

F (x)

can result if the variables are scaled before the functions to evaluate

F (x)

are coded. For instance, in the above problem just mentioned of Gaussian curve-fitting,

x_{3}

may always occur in terms of the form

(x_{3} - x_{m})

, where

x_{m}

is a constant representing the mean peak position.

The objective function has already been mentioned in the discussion of scaling the variables. The solution of a given problem is unaltered if

F (x)

is multiplied by a positive constant, or if a constant value is added to

F (x)

. It is generally preferable for the objective function to be of the order of unity in the region of interest; thus, if in the original formulation

F (x)

is always of the order of

10^{+ 5}

(say), then the value of

F (x)

should be multiplied by

10^{- 5}

when evaluating the function within an optimization function. If a constant is added or subtracted in the computation of

F (x)

, usually it should be omitted, i.e., it is better to formulate

F (x)

as

x_{1}^{2} + x_{2}^{2}

rather than as

x_{1}^{2} + x_{2}^{2} + 1000

or even

x_{1}^{2} + x_{2}^{2} + 1

. The inclusion of such a constant in the calculation of

F (x)

can result in a loss of significant figures.

A ‘well scaled’ set of constraints has two main properties. Firstly, each constraint should be well-conditioned with respect to perturbations of the variables. Secondly, the constraints should be balanced with respect to each other, i.e., all the constraints should have ‘equal weight’ in the solution process.

The solution of a linearly- or nonlinearly-constrained problem is unaltered if the

i

th constraint is multiplied by a positive weight

w_{i}

. At the approximation of the solution determined by a Library function, any active linear constraints will (in general) be satisfied ‘exactly’ (i.e., to within the tolerance defined by machine precision) if they have been properly scaled. This is in contrast to any active nonlinear constraints, which will not (in general) be satisfied ‘exactly’ but will have ‘small’ values (for example,

{\hat{c}}_{1} (x^{*}) = 10^{- 8}

,

{\hat{c}}_{2} (x^{*}) = {- 10}^{- 6}

, and so on). In general, this discrepancy will be minimized if the constraints are weighted so that a unit change in

x

produces a similar change in each constraint.

A second reason for introducing weights is related to the effect of the size of the constraints on the Lagrange multiplier estimates and, consequently, on the active set strategy. This means that different sets of weights may cause an algorithm to produce different sequences of iterates. Additional discussion is given in Gill et al. (1981).

The convergence criteria inevitably vary from function to function, since in some cases more information is available to be checked (for example, is the Hessian matrix positive definite?), and different checks need to be made for different problem categories (for example, in constrained minimization it is necessary to verify whether a trial solution is feasible). Nonetheless, the underlying principles of the various criteria are the same; in non-mathematical terms, they are:

(i)	is the sequence $\{x^{(k)}\}$ converging?
(ii)	is the sequence $\{F^{(k)}\}$ converging?
(iii)	are the necessary and sufficient conditions for the solution satisfied?

The decision as to whether a sequence is converging is necessarily speculative. The criterion used in the present functions is to assume convergence if the relative change occurring between two successive iterations is less than some prescribed quantity. Criterion (iii) is the most reliable but often the conditions cannot be checked fully because not all the required information may be available.

Little a priori guidance can be given as to the quality of the solution found by a nonlinear optimization algorithm, since no guarantees can be given that the methods will not fail. Therefore, you should always check the computed solution even if the function reports success. Frequently a ‘solution’ may have been found even when the function does not report a success. The reason for this apparent contradiction is that the function needs to assess the accuracy of the solution. This assessment is not an exact process and consequently may be unduly pessimistic. Any ‘solution’ is in general only an approximation to the exact solution, and it is possible that the accuracy you have specified is too stringent.

Further confirmation can be sought by trying to check whether or not convergence tests are almost satisfied, or whether or not some of the sufficient conditions are nearly satisfied. When it is thought that a function has returned a nonzero value of ifail only because the requirements for ‘success’ were too stringent it may be worth restarting with increased convergence tolerances.

For nonlinearly-constrained problems, check whether the solution returned is feasible, or nearly feasible; if not, the solution returned is not an adequate solution.

Confidence in a solution may be increased by resolving the problem with a different initial approximation to the solution. See Section 8.3 of Gill et al. (1981) for further information.

Many of the functions in the chapter have facilities to allow you to monitor the progress of the minimization process, and you are encouraged to make use of these facilities. Monitoring information can be a great aid in assessing whether or not a satisfactory solution has been obtained, and in indicating difficulties in the minimization problem or in the ability of the function to cope with the problem.

The behaviour of the function, the estimated solution and first derivatives can help in deciding whether a solution is acceptable and what to do in the event of a return with a nonzero value of ifail.

When estimates of the parameters in a nonlinear least squares problem have been found, it may be necessary to estimate the variances of the parameters and the fitted function. These can be calculated from the Hessian of

F (x)

at the solution.

In many least squares problems, the Hessian is adequately approximated at the solution by

G = 2 J^{T} J

(see Methods for nonlinear least squares problems). The Jacobian,

J

, or a factorization of

J

is returned by all the comprehensive least squares functions and, in addition, a function is available in the Library to estimate variances of the parameters following the use of most of the nonlinear least squares functions, in the case that

G = 2 J^{T} J

is an adequate approximation.

Let

H

be the inverse of

G

, and

S

be the sum of squares, both calculated at the solution

\bar{x}

; an unbiased estimate of the variance of the

i

th parameter

x_{i}

is

var {\bar{x}}_{i} = \frac{2 S}{m - n} H_{i i}

and an unbiased estimate of the covariance of

{\bar{x}}_{i}

and

{\bar{x}}_{j}

is

covar ({\bar{x}}_{i}, {\bar{x}}_{j}) = \frac{2 S}{m - n} H_{i j} .

If

x^{*}

is the true solution, then the

100 (1 - β) %

confidence interval on

\bar{x}

is

{\bar{x}}_{i} - \sqrt{var {\bar{x}}_{i}} . t_{(1 - β / 2, m - n)} < x_{i}^{*} < {\bar{x}}_{i} + \sqrt{var {\bar{x}}_{i}} . t_{(1 - β / 2, m - n)}, i = 1, 2, \dots, n

where

t_{(1 - β / 2, m - n)}

is the

100 (1 - β) / 2

percentage point of the

t

-distribution with

m - n

degrees of freedom.

In the majority of problems, the residuals

f_{i}

, for

i = 1, 2, \dots, m

, contain the difference between the values of a model function

ϕ (z, x)

calculated for

m

different values of the independent variable

z

, and the corresponding observed values at these points. The minimization process determines the parameters, or constants

x

, of the fitted function

ϕ (z, x)

. For any value,

\bar{z}

, of the independent variable

z

, an unbiased estimate of the variance of

ϕ

is

var ϕ = \frac{2 S}{m - n} \sum_{i = 1}^{n} \sum_{j = 1}^{n} {[\frac{\partial ϕ}{\partial x_{i}}]}_{\bar{z}} {[\frac{\partial ϕ}{\partial x_{j}}]}_{\bar{z}} H_{i j} .

The

100 (1 - β) %

confidence interval on

F

at the point

\bar{z}

is

ϕ (\bar{z}, \bar{x}) - \sqrt{var ϕ} . t_{(β / 2, m - n)} < ϕ (\bar{z}, x^{*}) < ϕ (\bar{z}, \bar{x}) + \sqrt{var ϕ} . t_{(β / 2, m - n)} .

For further details on the analysis of least squares solutions see Bard (1974) and Wolberg (1967).

The choice of function depends on several factors: the type of problem (unconstrained, etc.); the level of derivative information available (function values only, etc.); your experience (there are easy-to-use versions of some functions); whether or not storage is a problem; whether or not the function is to be used in a multithreaded environment; and whether computational time has a high priority. Not all choices are catered for in the current version of the Library.

Many functions appear in the Library in two forms: a comprehensive form and an easy-to-use form. The objective in the easy-to-use forms is to make the function simple to use by including in the calling sequence only those arguments absolutely essential to the definition of the problem, as opposed to arguments relevant to the solution method. If you are an experienced user the comprehensive functions have additional arguments which enable you to improve their efficiency by ‘tuning’ the method to a particular problem. If you are a casual or inexperienced user, this feature is of little value and may in some cases cause a failure because of a poor choice of some arguments.

In the easy-to-use functions, these extra arguments are determined either by fixing them at a known safe and reasonably efficient value, or by an auxiliary function which generates a ‘good’ value automatically.

For functions introduced since Mark 12 of the Library a different approach has been adopted towards the choice of easy-to-use and comprehensive functions. The optimization function has an easy-to-use argument list, but additional arguments may be changed from their default values by calling an ‘option’ setting function before the call to the main optimization function. This approach has the advantages of allowing the options to be given in the form of keywords and requiring only those options that are to be different from their default values to be set.

Most of the functions in this chapter are called just once in order to compute the minimum of a given objective function subject to a set of constraints on the variables. The objective function and nonlinear constraints (if any) are specified by you and written as functions to a very rigid format described in the relevant function document.

This chapter also contains a pair of reverse communication functions, nag_opt_nlp1_rcomm (e04uf), which solve dense NLP problems using a sequential quadratic programming method. These may be convenient to use when the minimization function is being called from a computer language which does not fully support procedure arguments in a way that is compatible with the Library. See Direct and Reverse Communication functions in Calling NAG Routines From MATLAB for more information about reverse communication functions.

One of the most common errors in the use of optimization functions is that user-supplied functions do not evaluate the relevant partial derivatives correctly. Because exact gradient information normally enhances efficiency in all areas of optimization, you are encouraged to provide analytical derivatives whenever possible. However, mistakes in the computation of derivatives can result in serious and obscure run-time errors. Consequently, service functions are provided to perform an elementary check on the gradients you supplied. These functions are inexpensive to use in terms of the number of calls they require to user-supplied functions.

The appropriate checking functions are as follows:

Minimization function	Checking function(s)
nag_opt_bounds_mod_deriv_comp (e04kd)	nag_opt_check_deriv (e04hc)
nag_opt_bounds_mod_deriv2_comp (e04lb)	nag_opt_check_deriv (e04hc) and nag_opt_check_deriv2 (e04hd)
nag_opt_lsq_uncon_quasi_deriv_comp (e04gb)	nag_opt_lsq_check_deriv (e04ya)
nag_opt_lsq_uncon_mod_deriv_comp (e04gd)	nag_opt_lsq_check_deriv (e04ya)
nag_opt_lsq_uncon_mod_deriv2_comp (e04he)	nag_opt_lsq_check_deriv (e04ya) and nag_opt_lsq_check_hessian (e04yb)

It should be noted that functions nag_opt_nlp1_rcomm (e04uf), nag_opt_lsq_gencon_deriv (e04us), nag_opt_nlp2_sparse_solve (e04vh) and nag_opt_nlp2_solve (e04wd) each incorporate a check on the gradients being supplied. This involves verifying the gradients at the first point that satisfies the linear constraints and bounds. There is also an option to perform a more reliable (but more expensive) check on the individual gradient elements being supplied. Note that the checks are not infallible.

A second type of service function computes a set of finite differences to be used when approximating first derivatives. Such differences are required as input arguments by some functions that use only function evaluations.

nag_opt_lsq_uncon_covariance (e04yc) estimates selected elements of the variance-covariance matrix for the computed regression parameters following the use of a nonlinear least squares function.

nag_opt_estimate_deriv (e04xa) estimates the gradient and Hessian of a function at a point, given a function to calculate function values only, or estimates the Hessian of a function at a point, given a function to calculate function and gradient values.

All the functions for constrained problems will ensure that any evaluations of the objective function occur at points which approximately satisfy any simple bounds or linear constraints. Satisfaction of such constraints is only approximate because functions which estimate derivatives by finite differences may require function evaluations at points which just violate such constraints even though the current iteration just satisfies them.

There is no attempt to ensure that the current iteration satisfies any nonlinear constraints. If you wish to prevent your objective function being evaluated outside some known region (where it may be undefined or not practically computable), you may try to confine the iteration within this region by imposing suitable simple bounds or linear constraints (but beware as this may create new local minima where these constraints are active).

Note also that some functions allow you to return the argument (iflag or mode) with a negative value to force an immediate clean exit from the minimization function when the objective function (or nonlinear constraints where appropriate) cannot be evaluated.

Apart from the standard types of optimization problem, there are other related problems which can be solved by functions in this or other chapters of the Library.

nag_mip_ilp_dense (h02bb) solves dense integer LP problems, nag_mip_iqp_dense (h02cb) solves dense integer QP problems, nag_mip_iqp_sparse (h02ce) solves sparse integer QP problems and nag_mip_transportation (h03ab) solves a special type of such problem known as a ‘transportation’ problem.

Several functions in Chapters F04 and F08 solve linear least squares problems, i.e.,

minimize \sum_{i = 1}^{m} r_{i} {(x)}^{2}

where

r_{i} (x) = b_{i} - \sum_{j = 1}^{n} a_{i j} x_{j}

.

nag_fit_glin_l1sol (e02ga) solves an overdetermined system of linear equations in the

l_{1}

norm, i.e., minimizes

\sum_{i = 1}^{m} |r_{i} (x)|

, with

r_{i}

as above, and nag_fit_glinc_l1sol (e02gb) solves the same problem subject to linear inequality constraints.

nag_fit_glin_linf (e02gc) solves an overdetermined system of linear equations in the

l_{\infty}

norm, i.e., minimizes

\max_{i} |r_{i} (x)|

, with

r_{i}

as above.

Chapter E05 contains functions for global minimization.

Methods for handling multi-objective optimization describes how a multi-objective optimization problem might be addressed using functions from this chapter and from Chapter E05.

As evidenced by the wide variety of functions available in Chapter E04, it is clear that no single algorithm can solve all optimization problems. It is important to try to match the problem to the most suitable function, and that is what the decision trees in Decision Trees help to do.

Sometimes in Chapter E04 more than one function is available to solve precisely the same minimization problem. Thus, for example, the general nonlinear programming functions nag_opt_nlp1_solve (e04uc) and nag_opt_nlp2_solve (e04wd) are based on similar methods. Experience shows that although both functions can usually solve the same problem and get similar results, sometimes one function will be faster, sometimes one might find a different local minimum to the other, or, in difficult cases, one function may obtain a solution when the other one fails.

After using one of these functions, if the results obtained are unacceptable for some reason, it may be worthwhile trying the other function instead. In the absence of any other information, in the first instance you are recommended to try using nag_opt_nlp1_solve (e04uc), and if that proves unsatisfactory, try using nag_opt_nlp2_solve (e04wd). Although the algorithms used are very similar, the two functions each have slightly different optional parameters which may allow the course of the computation to be altered in different ways.

Other pairs of functions which solve the same kind of problem are nag_opt_qpconvex2_sparse_solve (e04nq) (recommended first choice) or nag_opt_qpconvex1_sparse_solve (e04nk), for sparse quadratic or linear programming problems, and nag_opt_nlp1_sparse_solve (e04ug) or nag_opt_nlp2_sparse_solve (e04vh), for sparse nonlinear programming. In these cases the argument lists are not so similar as nag_opt_nlp1_solve (e04uc) or nag_opt_nlp2_solve (e04wd), but the same considerations apply.

Bard Y (1974) Nonlinear Parameter Estimation Academic Press

Dantzig G B (1963) Linear Programming and Extensions Princeton University Press

Fletcher R (1987) Practical Methods of Optimization (2nd Edition) Wiley

Gill P E and Murray W (ed.) (1974) Numerical Methods for Constrained Optimization Academic Press

Gill P E, Murray W and Wright M H (1981) Practical Optimization Academic Press

Murray W (ed.) (1972) Numerical Methods for Unconstrained Optimization Academic Press

Wolberg J R (1967) Prediction Analysis Van Nostrand

Is the linear constraint matrix sparse?			nag_opt_qpconvex2_sparse_solve (e04nq), nag_opt_qpconvex1_sparse_solve (e04nk), nag_opt_nlp2_sparse_solve (e04vh) and nag_opt_nlp1_sparse_solve (e04ug)
		yes
	no
Is the objective function linear (an LP problem)?			nag_opt_lp_solve (e04mf)
		yes
	no
Is the QP problem convex?			nag_opt_lsq_lincon_solve (e04nc)
		yes
	no
nag_opt_qp_dense_solve (e04nf)

NAG Toolbox Chapter IntroductionE04 — minimizing or maximizing a function

Scope of the Chapter

Background to the Problems

Types of Optimization Problems

Unconstrained minimization

Nonlinear least squares problems

Minimization subject to bounds on the variables

Minimization subject to linear constraints

Minimization subject to nonlinear constraints

Minimization subject to bounds on the objective function

Multi-objective optimization

Geometric Representation and Terminology

Gradient vector

Hessian matrix

Jacobian matrix; matrix of constraint normals

Sufficient Conditions for a Solution

Unconstrained minimization

Minimization subject to bounds on the variables

Linearly-constrained minimization

Nonlinearly-constrained minimization

Background to Optimization Methods

One-dimensional optimization

Methods for unconstrained optimization

Methods for nonlinear least squares problems

Methods for handling constraints

Methods for handling multi-objective optimization

Scaling

Transformation of variables

Scaling the objective function

Scaling the constraints

Analysis of Computed Results

Convergence criteria

Checking results

Monitoring progress

Confidence intervals for least squares solutions

Recommendations on Choice and Use of Available Functions

Easy-to-use and Comprehensive Functions

Reverse Communication Functions

Service Functions

Function Evaluations at Infeasible Points

Related Problems

Choosing Between Variant Functions for Some Problems

Decision Trees

Tree 1: Selection chart for unconstrained problems

Tree 2: Selection chart for bound-constrained, linearly-constrained and nonlinearly-constrained problems

Tree 3: Linear and Quadratic Programming (LP and QP)

Functionality Index

References

NAG Toolbox Chapter Introduction

E04 — minimizing or maximizing a function