PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_opt_uncon_simplex (e04cb)
Purpose
nag_opt_uncon_simplex (e04cb) minimizes a general function
of
independent variables
by the Nelder and Mead simplex method (see
Nelder and Mead (1965)). Derivatives of the function need not be supplied.
Syntax
[
x,
f,
user,
ifail] = e04cb(
x,
tolf,
tolx,
funct,
monit,
maxcal, 'n',
n, 'user',
user)
[
x,
f,
user,
ifail] = nag_opt_uncon_simplex(
x,
tolf,
tolx,
funct,
monit,
maxcal, 'n',
n, 'user',
user)
Description
nag_opt_uncon_simplex (e04cb) finds an approximation to a minimum of a function of variables. You must supply a function to calculate the value of for any set of values of the variables.
The method is iterative. A simplex of
points is set up in the
-dimensional space of the variables (for example, in
dimensions the simplex is a triangle) under the assumption that the problem has been scaled so that the values of the independent variables at the minimum are of order unity. The starting point you have provided is the first vertex of the simplex, the remaining
vertices are generated by
nag_opt_uncon_simplex (e04cb). The vertex of the simplex with the largest function value is reflected in the centre of gravity of the remaining vertices and the function value at this new point is compared with the remaining function values. Depending on the outcome of this test the new point is accepted or rejected, a further expansion move may be made, or a contraction may be carried out. See
Nelder and Mead (1965) and
Parkinson and Hutchinson (1972) for more details. When no further progress can be made the sides of the simplex are reduced in length and the method is repeated.
The method can be slow, but computational bottlenecks have been reduced following
Singer and Singer (2004). However,
nag_opt_uncon_simplex (e04cb) is robust, and therefore very useful for functions that are subject to inaccuracies.
There are the following options for successful termination of the method: based only on the function values at the vertices of the current simplex (see
(1)); based only on a volume ratio between the current simplex and the initial one (see
(2)); or based on which one of the previous two tests passes first. The volume test may be useful if
is discontinuous, while the function-value test should be sufficient on its own if
is continuous.
References
Nelder J A and Mead R (1965) A simplex method for function minimization Comput. J. 7 308–313
Parkinson J M and Hutchinson D (1972) An investigation into the efficiency of variants of the simplex method Numerical Methods for Nonlinear Optimization (ed F A Lootsma) Academic Press
Singer S and Singer S (2004) Efficient implementation of the Nelder–Mead search algorithm Appl. Num. Anal. Comp. Math. 1(3) 524–534
Parameters
Compulsory Input Parameters
- 1:
– double array
-
A guess at the position of the minimum. Note that the problem should be scaled so that the values of the are of order unity.
- 2:
– double scalar
-
The error tolerable in the function values, in the following sense. If
, for
, are the individual function values at the vertices of the current simplex, and if
is the mean of these values, then you can request that
nag_opt_uncon_simplex (e04cb) should terminate if
You may specify
if you wish to use only the termination criterion
(2) on the spatial values: see the description of
tolx.
Constraint:
must be greater than or equal to the
machine precision (see
Chapter X02), or if
tolf equals zero then
tolx must be greater than or equal to the
machine precision.
- 3:
– double scalar
-
The error tolerable in the spatial values, in the following sense. If
denotes the ‘linearized’ volume of the current simplex, and if
denotes the ‘linearized’ volume of the initial simplex, then you can request that
nag_opt_uncon_simplex (e04cb) should terminate if
You may specify
if you wish to use only the termination criterion
(1) on function values: see the description of
tolf.
Constraint:
must be greater than or equal to the
machine precision (see
Chapter X02), or if
tolx equals zero then
tolf must be greater than or equal to the
machine precision.
- 4:
– function handle or string containing name of m-file
-
funct must evaluate the function
at a specified point. It should be tested separately before being used in conjunction with
nag_opt_uncon_simplex (e04cb).
[fc, user] = funct(n, xc, user)
Input Parameters
- 1:
– int64int32nag_int scalar
-
, the number of variables.
- 2:
– double array
-
The point at which the function value is required.
- 3:
– Any MATLAB object
funct is called from
nag_opt_uncon_simplex (e04cb) with the object supplied to
nag_opt_uncon_simplex (e04cb).
Output Parameters
- 1:
– double scalar
-
The value of the function at the current point .
- 2:
– Any MATLAB object
- 5:
– function handle or string containing name of m-file
-
monit may be used to monitor the optimization process. It is invoked once every iteration.
If no monitoring is required,
monit may be string
nag_opt_uncon_simplex_dummy_monit (e04cbk)
[user] = monit(fmin, fmax, sim, n, ncall, serror, vratio, user)
Input Parameters
- 1:
– double scalar
-
The smallest function value in the current simplex.
- 2:
– double scalar
-
The largest function value in the current simplex.
- 3:
– double array
-
The position vectors of the current simplex.
- 4:
– int64int32nag_int scalar
-
, the number of variables.
- 5:
– int64int32nag_int scalar
-
The number of times that
funct has been called so far.
- 6:
– double scalar
-
The current value of the standard deviation in function values used in termination test
(1).
- 7:
– double scalar
-
The current value of the linearized volume ratio used in termination test
(2).
- 8:
– Any MATLAB object
monit is called from
nag_opt_uncon_simplex (e04cb) with the object supplied to
nag_opt_uncon_simplex (e04cb).
Output Parameters
- 1:
– Any MATLAB object
- 6:
– int64int32nag_int scalar
-
The maximum number of function evaluations to be allowed.
Constraint:
.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the array
x.
, the number of variables.
Constraint:
.
- 2:
– Any MATLAB object
user is not used by
nag_opt_uncon_simplex (e04cb), but is passed to
funct and
monit. Note that for large objects it may be more efficient to use a global variable which is accessible from the m-files than to use
user.
Output Parameters
- 1:
– double array
-
The value of
corresponding to the function value in
f.
- 2:
– double scalar
-
The lowest function value found.
- 3:
– Any MATLAB object
- 4:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
Constraint: if
and
then both should be greater than or equal to the
machine precision.
Constraint: if
then
is greater than or equal to the
machine precision.
Constraint: if
then
is greater than or equal to the
machine precision.
Constraint: .
Constraint: .
-
-
maxcal function evaluations have been completed without any other termination test passing. Check the coding of
funct before increasing the value of
maxcal.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
On a successful exit the accuracy will be as defined by
tolf or
tolx, depending on which criterion was satisfied first.
Further Comments
Local workspace arrays of fixed lengths (depending on
n) are allocated internally by
nag_opt_uncon_simplex (e04cb). The total size of these arrays amounts to
double elements.
The time taken by nag_opt_uncon_simplex (e04cb) depends on the number of variables, the behaviour of the function and the distance of the starting point from the minimum. Each iteration consists of or function evaluations unless the size of the simplex is reduced, in which case function evaluations are required.
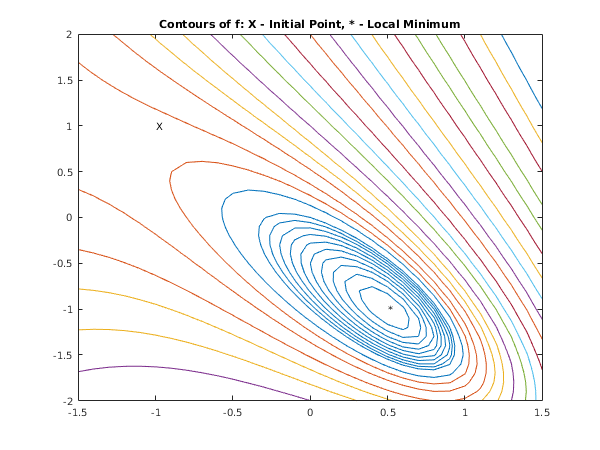
Example
This example finds a minimum of the function
This example uses the initial point and we expect to reach the minimum at .
Open in the MATLAB editor:
e04cb_example
function e04cb_example
fprintf('e04cb example results\n\n');
global print_info
print_info = false;
x0 = [-1; 1];
tolf = sqrt(x02aj);
tolx = sqrt(tolf);
maxcal = int64(100);
[x, f, user, ifail] = e04cb( ...
x0, tolf, tolx, @funct, @monit, maxcal);
fprintf('Minimum function value = %12.3e\n',f);
fprintf('Minumum location, x = (%7.3f,%7.3f)\n',x);
fig1 = figure;
[xx,yy] = meshgrid([-1.5:0.1:1.5],[-2:0.1:2]);
z = exp(xx).*(4*xx.*(xx+yy)+2*yy.*(yy+1)+1);
[~,h] = contour(xx,yy,z);
h.LevelList = [0:0.1:1,1.3,1.6,2,2.6,3.2,4,5,6.5,8,10, ...
13,16,20,25,32,40,50,65,80,100];
colormap(lines);
text(x(1),x(2),'*');
text(x0(1),x0(2),'X');
title('Contours of f: X - Initial Point, * - Local Minimum');
function [fc, user] = funct(n, xc, user)
fc = exp(xc(1))*(4*xc(1)*(xc(1)+xc(2))+2*xc(2)*(xc(2) +1)+1);
function [user] = monit(fmin, fmax, sim, n, ncall, serror, vratio, user)
global print_info
if (print_info)
fprintf('\nNumber of function calls = %10d\n', ncall);
fprintf('Smallest function value = %10.6f\n', fmin);
fprintf('The simplex is\n');
disp(sim);
fprintf('Standard deviation in f(vertices) = %10.6f\n', serror);
fprintf('Current/initial simplex volume ratio = %10.6f\n', vratio);
end
e04cb example results
Minimum function value = 1.789e-08
Minumum location, x = ( 0.500, -1.000)
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015