PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox Chapter Introduction
D02MN — integrators for stiff ordinary differential systems
Introduction
This sub-chapter contains the specifications of the integrators, the setup functions and diagnostic functions which have been developed from the
SPRINT package,
Berzins and Furzeland (1985), and from the
DASSL package,
Brenan et al. (1996).
The SPRINT explicit integrators
nag_ode_ivp_stiff_exp_fulljac (d02nb),
nag_ode_ivp_stiff_exp_bandjac (d02nc) and
nag_ode_ivp_stiff_exp_sparjac (d02nd) are designed for solving stiff systems of explicitly defined ordinary differential equations,
The SPRINT implicit integrators
nag_ode_ivp_stiff_imp_fulljac (d02ng),
nag_ode_ivp_stiff_imp_bandjac (d02nh) and
nag_ode_ivp_stiff_imp_sparjac (d02nj) are designed for solving stiff systems of implicitly defined ordinary differential equations,
The DASSL integrator
nag_ode_dae_dassl_gen (d02ne) is designed for solving systems of the form,
. These formulations permits solution of differential/algebraic systems
(DAEs). The facilities provided are essentially those of the explicit solvers.
The SPRINT integrator functions have almost identical calling sequences but each is designed to solve a problem where the Jacobian is of a particular structure: full matrix (
nag_ode_ivp_stiff_exp_fulljac (d02nb) and
nag_ode_ivp_stiff_imp_fulljac (d02ng)), banded matrix (
nag_ode_ivp_stiff_exp_bandjac (d02nc) and
nag_ode_ivp_stiff_imp_bandjac (d02nh)) or sparse matrix (
nag_ode_ivp_stiff_exp_sparjac (d02nd) and
nag_ode_ivp_stiff_imp_sparjac (d02nj)). Each of these structures has associated with it a linear algebra setup function:
nag_ode_ivp_stiff_fulljac_setup (d02ns),
nag_ode_ivp_stiff_bandjac_setup (d02nt) and
nag_ode_ivp_stiff_sparjac_setup (d02nu) respectively. A linear algebra setup function must be called before the first call to the appropriate integrator. These linear algebra setup functions check various arguments of the corresponding integrator function and set certain arguments for the linear algebra computations. A function,
nag_ode_ivp_stiff_sparjac_diag (d02nx), is supplied which permits extraction of diagnostic information after a call to either of the sparse linear algebra solvers
nag_ode_ivp_stiff_exp_sparjac (d02nd) and
nag_ode_ivp_stiff_imp_sparjac (d02nj).
With the SPRINT integrators are also associated three integrator setup functions
nag_ode_ivp_stiff_dassl (d02mv),
nag_ode_ivp_stiff_bdf (d02nv) and
nag_ode_ivp_stiff_blend (d02nw), one of which must be called before the first call to any integrator function. They provide input to the Backward Differentiation Formulae (BDF), the Blend Formulae and the special fixed leading coefficient BDF codes respectively. On return from an integrator, if it is feasible to continue the integration,
nag_ode_ivp_stiff_contin (d02nz) may be called to reset various integration arguments. It is often of considerable interest to determine statistics concerning the integration process.
nag_ode_ivp_stiff_integ_diag (d02ny) is provided with this aim in mind. It should prove especially useful to those who wish to integrate many similar problems as it provides suitable values for many of the input arguments and indications of the difficulties encountered when solving the problem.
Hence, the general form of a program calling one of the integrator functions
nag_ode_ivp_stiff_exp_fulljac (d02nb),
nag_ode_ivp_stiff_exp_bandjac (d02nc),
nag_ode_ivp_stiff_exp_sparjac (d02nd),
nag_ode_ivp_stiff_imp_fulljac (d02ng),
nag_ode_ivp_stiff_imp_bandjac (d02nh) or
nag_ode_ivp_stiff_imp_sparjac (d02nj)
will be
.
.
call linear algebra setup routine
call integrator setup routine
call integrator
call integrator diagnostic routine (if required)
call linear algebra diagnostic routine (if appropriate and if required)
.
.
The DASSL integrator,
nag_ode_dae_dassl_gen (d02ne), has an associated setup function
nag_ode_dae_dassl_setup (d02mw) which must be called first. On return from the integrator, if it is feasible to continue the integration, the associated continuation call function is
nag_ode_dae_dassl_cont (d02mc) may be called to rest various integration parameters. The structure of the Jacobian is assumed to be full unless
nag_ode_dae_dassl_linalg (d02np) is called following a call to the setup function to specify that the Jacobian is banded and to supply its bandwidths.
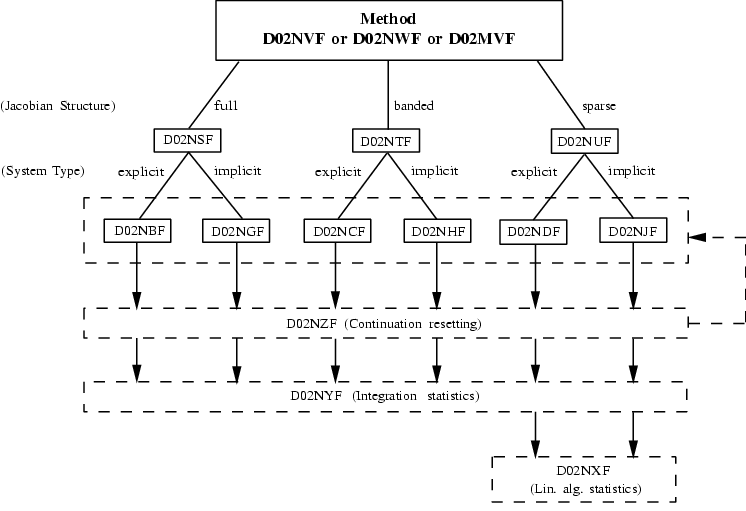
The required calling sequence for different Jacobian structures and system types is represented diagrammatically in
Figure 1.
Figure 1: Schema for SPRINT forward communication function calling sequences
The integrators
nag_ode_ivp_stiff_exp_revcom (d02nm) and
nag_ode_ivp_stiff_imp_revcom (d02nn) are reverse communication functions designed for solving explicit and implicit stiff ordinary differential systems respectively. You are warned that you should use these functions only when the integrators mentioned above are inadequate for their application. For example, if it is difficult to write one or more of the user-supplied function
fcn (
resid) or
jac (or
monitr) or if the integrators are to be embedded in a package, it may be advisable to consider these functions.
Since these functions use reverse communication you do not need to define any functions with a prescribed argument list. This makes them especially suitable for large scale computations where encapsulation of the definition of the differential system or its Jacobian matrix in a prescribed function form may be particularly difficult to achieve.
nag_ode_ivp_stiff_exp_revcom (d02nm) is the reverse communication counterpart of the forward communication functions
nag_ode_ivp_stiff_exp_fulljac (d02nb),
nag_ode_ivp_stiff_exp_bandjac (d02nc) and
nag_ode_ivp_stiff_exp_sparjac (d02nd) whereas
nag_ode_ivp_stiff_imp_revcom (d02nn) is the reverse communication counterpart of the forward communication functions
nag_ode_ivp_stiff_imp_fulljac (d02ng),
nag_ode_ivp_stiff_imp_bandjac (d02nh) and
nag_ode_ivp_stiff_imp_sparjac (d02nj). When using these reverse communication functions it is necessary to call the same linear algebra and integrator setup functions as for the forward communication counterpart. All the other continuation and interrogation functions available for use with the forward communication functions are also available to you when calling the reverse communication functions.
There is also a function,
nag_ode_ivp_stiff_sparjac_enq (d02nr), to tell you how to supply the Jacobian when the sparse linear algebra option is being employed with either of
nag_ode_ivp_stiff_exp_revcom (d02nm) and
nag_ode_ivp_stiff_imp_revcom (d02nn). Hence, the general form of a program calling one of the integrator functions
nag_ode_ivp_stiff_exp_revcom (d02nm) or
nag_ode_ivp_stiff_imp_revcom (d02nn) will be
call linear algebra setup routine
call integrator setup routine
irevcm = int32(0);
call integrator( ..., irevcm, ...)
while (irevcm > 0)
evaluate residual and Jacobian (including a call to d02nr if
sparse linear algebra is being used), call the monitr routine etc.
call integrator( ..., irevcm, ...)
end
call integrator diagnostic routine (if required)
call linear algebra diagnostic routine (if appropriate and if required)
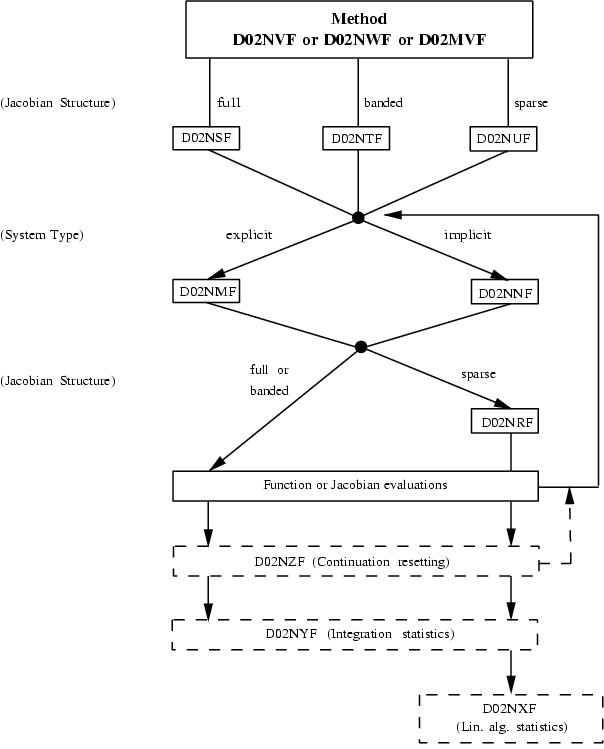
The required calling sequence in the case of reverse communication, is represented diagramatically in
Figure 2.
In the example programs for the eight SPRINT integrators
nag_ode_ivp_stiff_exp_fulljac (d02nb),
nag_ode_ivp_stiff_exp_bandjac (d02nc),
nag_ode_ivp_stiff_exp_sparjac (d02nd),
nag_ode_ivp_stiff_imp_fulljac (d02ng),
nag_ode_ivp_stiff_imp_bandjac (d02nh),
nag_ode_ivp_stiff_imp_sparjac (d02nj),
nag_ode_ivp_stiff_exp_revcom (d02nm) and
nag_ode_ivp_stiff_imp_revcom (d02nn) we attempt to illustrate the various options available. Many of these options are available in all the functions and you are invited to scan all the example programs for illustrations of their use. In each case we use as an example the stiff Robertson problem
despite the fact that it is not a sensible choice to use either the banded or the sparse linear algebra for this problem. Their use here serves for illustration of the techniques involved. For the implicit integrators
nag_ode_ivp_stiff_imp_fulljac (d02ng),
nag_ode_ivp_stiff_imp_bandjac (d02nh) and
nag_ode_ivp_stiff_imp_sparjac (d02nj)
we write the Robertson problem in residual form, as an implicit differential system and as a differential/algebraic system respectively. Here we are exploiting the fact that
is constant and hence one of the equations may be replaced by
or
(for our particular choice of initial conditions). For the reverse communication functions
nag_ode_ivp_stiff_exp_revcom (d02nm) and
nag_ode_ivp_stiff_imp_revcom (d02nn) our examples are intended only to illustrate the reverse communication technique.
Figure 2: Schema for SPRINT reverse communication function calling sequences
The DASSL integrator
nag_ode_dae_dassl_gen (d02ne) can solve DAEs of the fully implicit form
and therefore has increased functionality over the SPRINT integrators. Additionally
nag_ode_dae_dassl_gen (d02ne) can be used to solve difficult algebraic problems by continuation; for example, the nonlinear algebraic problem
can be solved by integrating solutions of
where the solution to
is known. The solution of this type of problem is illustrated in
Example in
nag_ode_dae_dassl_gen (d02ne).
References
Berzins M and Furzeland R M (1985) A user's manual for SPRINT – A versatile software package for solving systems of algebraic, ordinary and partial differential equations: Part 1 – Algebraic and ordinary differential equations Report TNER.85.085 Shell Research Limited
Brenan K, Campbell S and Petzold L (1996) Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations SIAM, Philadelphia
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015