PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_ode_ivp_stiff_exp_revcom (d02nm)
Purpose
nag_ode_ivp_stiff_exp_revcom (d02nm) is a reverse communication function for integrating stiff systems of explicit ordinary differential equations.
Syntax
[
t,
y,
ydot,
rwork,
inform,
ysav,
wkjac,
jacpvt,
imon,
inln,
ires,
irevcm,
ifail] = d02nm(
t,
tout,
y,
ydot,
rwork,
rtol,
atol,
itol,
inform,
ysav,
wkjac,
jacpvt,
imon,
inln,
ires,
irevcm,
itask,
itrace, 'neq',
neq, 'sdysav',
sdysav, 'nwkjac',
nwkjac)
[
t,
y,
ydot,
rwork,
inform,
ysav,
wkjac,
jacpvt,
imon,
inln,
ires,
irevcm,
ifail] = nag_ode_ivp_stiff_exp_revcom(
t,
tout,
y,
ydot,
rwork,
rtol,
atol,
itol,
inform,
ysav,
wkjac,
jacpvt,
imon,
inln,
ires,
irevcm,
itask,
itrace, 'neq',
neq, 'sdysav',
sdysav, 'nwkjac',
nwkjac)
Note: the interface to this routine has changed since earlier releases of the toolbox:
| At Mark 22: |
njcpvt was removed from the interface; neq was made optional |
Description
nag_ode_ivp_stiff_exp_revcom (d02nm) is a general purpose function for integrating the initial value problem for a stiff system of explicit ordinary differential equations,
An outline of a typical calling program is given below:
%
% data initialization
%
call linear algebra setup routine
call integrator setup routine
irevcm = int32(0);
[..., irevcm, ...] = d02nm();
while (irevcm > 0)
if (irevcm == 8)
supply the jacobian matrix (i)
elseif (irevcm == 9)
perform monitoring tasks requested by the user (ii)
elseif (irecvm == 1 or irevcm >= 3 and irevcm <= 5)
evaluate the derivative (iii)
elseif (irevcm == 10)
indicates an unsuccessful step
end
[..., irevcm, ...] = d02nm();
end
%
% post processing (optional linear algebra diagnostic call
% (sparse case only), optional integrator diagnostic call)
%There are three major operations that may be required of the calling (sub)program on an intermeditate return () from nag_ode_ivp_stiff_exp_revcom (d02nm); these are denoted (i), (ii) and (iii) above.
The following sections describe in greater detail exactly what is required of each of these operations.
(i) Supply the Jacobian Matrix
You need only provide this facility if the argument
(or
if using sparse matrix linear algebra) in a call to the linear algebra setup function (see
jceval in
nag_ode_ivp_stiff_fulljac_setup (d02ns)). If the Jacobian matrix is to be evaluated numerically by the integrator, then the remainder of section (i) can be ignored.
We must define the system of nonlinear equations which is solved internally by the integrator. The time derivative,
, has the form
where
is the current step size and
is a argument that depends on the integration method in use. The vector
is the current solution and the vector
depends on information from previous time steps. This means that
.
The system of nonlinear equations that is solved has the form
but is solved in the form
where the function
is defined by
It is the Jacobian matrix
that you must supply as follows:
where
,
and
are located in
,
and
respectively and the array
y contains the current values of the dependent variables. Only the nonzero elements of the Jacobian need be set, since the locations where it is to be stored are preset to zero.
Hereafter in this document this operation will be referred to as JAC.
(ii) Perform Tasks Requested by You
This operation is essentially a monitoring function and additionally provides the opportunity of changing the current values of
y, HNEXT (the step size that the integrator proposes to take on the next step), HMIN (the minimum step size to be taken on the next step), and HMAX (the maximum step size to be taken on the next step). The scaled local error at the end of a timestep may be obtained by calling double function
nag_ode_ivp_stiff_errest (d02za) as follows:
[errloc, ifail] = d02za(rwork(51+neq:51+neq+neq-1), rwork(51:51+neq-1));
% Check ifail before proceeding
The following gives details of the location within the array
rwork of variables that may be of interest to you:
| Variable |
Specification |
Location |
| tcurr |
the current value of the independent variable |
|
| hlast |
last step size successfully used by the integrator |
|
| hnext |
step size that the integrator proposes to take on the next step |
|
| hmin |
minimum step size to be taken on the next step |
|
| hmax |
maximum step size to be taken on the next step |
|
| nqu |
the order of the integrator used on the last step |
|
You are advised to consult the description of
monitr in
nag_ode_ivp_stiff_exp_fulljac (d02nb) for details on what optional input can be made.
If
y is changed, then
imon must be set to
before return to
nag_ode_ivp_stiff_exp_revcom (d02nm). If either of the values of HMIN or HMAX are changed, then
imon must be set
before return to
nag_ode_ivp_stiff_exp_revcom (d02nm). If HNEXT is changed, then
imon must be set to
before return to
nag_ode_ivp_stiff_exp_revcom (d02nm).
In addition you can force
nag_ode_ivp_stiff_exp_revcom (d02nm) to evaluate the residual vector
by setting
and
and then returning to
nag_ode_ivp_stiff_exp_revcom (d02nm); on return to this monitoring operation the residual vector will be stored in
, for
.
Hereafter in this document this operation will be referred to as MONITR.
(iii) Evaluate the Derivative
This operation must evaluate the derivative vector for the explicit ordinary differential equation system defined by
where
is located in
.
Hereafter in this document this operation will be referred to as FCN.
References
Parameters
Note: this function uses
reverse communication. Its use involves an initial entry, intermediate exits and re-entries, and a final exit, as indicated by the argument
irevcm. Between intermediate exits and re-entries,
all arguments other than ydot, rwork, wkjac, imon, inln and ires must remain unchanged.
Compulsory Input Parameters
- 1:
– double scalar
-
On initial entry:
, the value of the independent variable. The input value of
t is used only on the first call as the initial point of the integration.
- 2:
– double scalar
-
On initial entry: the next value of
at which a computed solution is desired. For the initial
, the input value of
tout is used to determine the direction of integration. Integration is permitted in either direction (see also
itask).
Constraint:
.
- 3:
– double array
-
On initial entry: the values of the dependent variables (solution). On the first call the first
neq elements of
must contain the vector of initial values.
- 4:
– double array
-
On intermediate re-entry: must be set to the derivatives as defined under the description of
irevcm.
- 5:
– double array
-
On initial entry: must be the same array as used by one of the method setup functions
nag_ode_ivp_stiff_dassl (d02mv),
nag_ode_ivp_stiff_bdf (d02nv) or
nag_ode_ivp_stiff_blend (d02nw), and by one of the storage setup functions
nag_ode_ivp_stiff_bandjac_setup (d02nt),
nag_ode_ivp_stiff_sparjac_setup (d02nu) or
nag_ode_ivp_stiff_bdf (d02nv). The contents of
rwork must not be changed between any call to a setup function and the first call to
nag_ode_ivp_stiff_exp_revcom (d02nm).
On intermediate re-entry: elements of
rwork must be set to quantities as defined under the description of
irevcm.
- 6:
– double array
-
The dimension of the array
rtol
must be at least
if
or
, and at least
otherwise
On initial entry: the relative local error tolerance.
Constraint:
for all relevant
(see
itol).
- 7:
– double array
-
The dimension of the array
atol
must be at least
if
or
, and at least
otherwise
On initial entry: the absolute local error tolerance.
Constraint:
for all relevant
(see
itol).
- 8:
– int64int32nag_int scalar
-
On initial entry: a value to indicate the form of the local error test.
itol indicates to
nag_ode_ivp_stiff_exp_revcom (d02nm) whether to interpret either or both of
rtol or
atol as a vector or a scalar. The error test to be satisfied is
, where
is defined as follows:
| itol | rtol | atol | |
| 1 | scalar | scalar | |
| 2 | scalar | vector | |
| 3 | vector | scalar | |
| 4 | vector | vector | |
is an estimate of the local error in , computed internally, and the choice of norm to be used is defined by a previous call to an integrator setup function.
Constraint:
, , or .
- 9:
– int64int32nag_int array
-
- 10:
– double array
-
ldysav, the first dimension of the array, must satisfy the constraint
.
On initial entry: the second dimension of the array
ysav. an appropriate value for
sdysav is described in the specifications of the integrator setup functions
nag_ode_ivp_stiff_bdf (d02nv) and
nag_ode_ivp_stiff_blend (d02nw). This value must be the same as that supplied to the integrator setup function.
- 11:
– double array
-
On intermediate re-entry: elements of the Jacobian as defined under the description of
irevcm. If a numerical Jacobian was requested then
wkjac is used for workspace.
- 12:
– int64int32nag_int array
-
On initial entry: the dimension of the array
jacpvt. the actual size depends on the linear algebra method used. An appropriate value for
njcpvt is described in the specifications of the linear algebra setup functions
nag_ode_ivp_stiff_bandjac_setup (d02nt) and
nag_ode_ivp_stiff_sparjac_setup (d02nu) for banded and sparse matrix linear algebra respectively. This value must be the same as that supplied to the linear algebra setup function. When full matrix linear algebra is chosen, the array
jacpvt is not used and hence
njcpvt should be set to
.
- 13:
– int64int32nag_int scalar
-
On intermediate re-entry: may be reset to determine subsequent action in
nag_ode_ivp_stiff_exp_revcom (d02nm).
- Integration is to be halted. A return will be made from nag_ode_ivp_stiff_exp_revcom (d02nm) to the calling (sub)program with .
- Allow nag_ode_ivp_stiff_exp_revcom (d02nm) to continue with its own internal strategy. The integrator will try up to three restarts unless .
- Return to the internal nonlinear equation solver, where the action taken is determined by the value of inln.
- Normal exit to nag_ode_ivp_stiff_exp_revcom (d02nm) to continue integration.
- Restart the integration at the current time point. The integrator will restart from order when this option is used. The solution y, provided by the monitr operation (see Description), will be used for the initial conditions.
- Try to continue with the same step size and order as was to be used before entering the monitr operation (see Description). hmin and hmax may be altered if desired.
- Continue the integration but using a new value of hnext and possibly new values of hmin and hmax.
- 14:
– int64int32nag_int scalar
-
On intermediate re-entry: with
and
,
inln specifies the action to be taken by the internal nonlinear equation solver. By setting
and returning to
nag_ode_ivp_stiff_exp_revcom (d02nm), the residual vector is evaluated and placed in
, for
and then the
monitr operation (see
Description) is invoked again. At present this is the only option available:
inln must not be set to any other value.
- 15:
– int64int32nag_int scalar
-
On intermediate re-entry: should be unchanged unless one of the following actions is required of
nag_ode_ivp_stiff_exp_revcom (d02nm) in which case
ires should be set accordingly.
- Indicates to nag_ode_ivp_stiff_exp_revcom (d02nm) that control should be passed back immediately to the calling (sub)program with the error indicator set to .
- Indicates to nag_ode_ivp_stiff_exp_revcom (d02nm) that an error condition has occurred in the solution vector, its time derivative or in the value of . The integrator will use a smaller time step to try to avoid this condition. If this is not possible nag_ode_ivp_stiff_exp_revcom (d02nm) returns to the calling (sub)program with the error indicator set to .
- Indicates to nag_ode_ivp_stiff_exp_revcom (d02nm) to stop its current operation and to enter the monitr operation (see Description) immediately.
- 16:
– int64int32nag_int scalar
-
On initial entry: must contain .
On intermediate re-entry: should remain unchanged.
Constraint:
, , , , , , or .
- 17:
– int64int32nag_int scalar
-
On initial entry: the task to be performed by the integrator.
- Normal computation of output values of at (by overshooting and interpolating).
- Take one step only and return.
- Stop at the first internal integration point at or beyond and return.
- Normal computation of output values of at but without overshooting . tcrit must be specified as an option in one of the integrator setup functions before the first call to the integrator, or specified in the optional input function before a continuation call. tcrit (e.g., see nag_ode_ivp_stiff_bdf (d02nv)) may be equal to or beyond tout, but not before it in the direction of integration.
- Take one step only and return, without passing tcrit (e.g., see nag_ode_ivp_stiff_bdf (d02nv)). tcrit must be specified under .
Constraint:
.
- 18:
– int64int32nag_int scalar
-
On initial entry: the level of output that is printed by the integrator.
itrace may take the value
,
,
,
or
.
- is assumed and similarly if , then is assumed.
- No output is generated.
- Only warning messages are printed on the current error message unit (see nag_file_set_unit_error (x04aa)).
- Warning messages are printed as above, and on the current advisory message unit (see nag_file_set_unit_advisory (x04ab)) output is generated which details Jacobian entries, the nonlinear iteration and the time integration. The advisory messages are given in greater detail the larger the value of itrace.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the arrays
y,
ydot and the first dimension of the array
ysav. (An error is raised if these dimensions are not equal.)
On initial entry: the number of differential equations to be solved.
Constraint:
.
- 2:
– int64int32nag_int scalar
-
Default:
the second dimension of the array
ysav.
On initial entry: the second dimension of the array
ysav. an appropriate value for
sdysav is described in the specifications of the integrator setup functions
nag_ode_ivp_stiff_bdf (d02nv) and
nag_ode_ivp_stiff_blend (d02nw). This value must be the same as that supplied to the integrator setup function.
- 3:
– int64int32nag_int scalar
-
Default:
the dimension of the array
wkjac.
On initial entry: the dimension of the array
wkjac. the actual size depends on the linear algebra method used. An appropriate value for
nwkjac is described in the specifications of the linear algebra setup functions
nag_ode_ivp_stiff_fulljac_setup (d02ns),
nag_ode_ivp_stiff_bandjac_setup (d02nt) and
nag_ode_ivp_stiff_sparjac_setup (d02nu) for full, banded and sparse matrix linear algebra respectively. This value must be the same as that supplied to the linear algebra setup function.
Output Parameters
- 1:
– double scalar
-
On final exit: the value at which the computed solution
is returned (usually at
tout).
- 2:
– double array
-
On final exit: the computed solution vector evaluated at
t (usually
).
- 3:
– double array
-
On final exit: the time derivatives of the vector at the last integration point.
- 4:
– double array
-
On intermediate exit:
contains information for JAC, FCN and MONITR operations as described in
Description and the argument
irevcm.
- 5:
– int64int32nag_int array
-
- 6:
– double array
-
- 7:
– double array
-
On intermediate exit:
the Jacobian is overwritten.
- 8:
– int64int32nag_int array
-
- 9:
– int64int32nag_int scalar
-
On intermediate exit:
used to pass information between
nag_ode_ivp_stiff_exp_revcom (d02nm) and the MONITR operation (see
Description). With
,
imon contains a flag indicating under what circumstances the return from
nag_ode_ivp_stiff_exp_revcom (d02nm) occurred:
- Exit from nag_ode_ivp_stiff_exp_revcom (d02nm) after caused an early termination (this facility could be used to locate discontinuities).
- The current step failed repeatedly.
- Exit from nag_ode_ivp_stiff_exp_revcom (d02nm) after a call to the internal nonlinear equation solver.
- The current step was successful.
- 10:
– int64int32nag_int scalar
-
On intermediate exit:
contains a flag indicating the action to be taken, if any, by the internal nonlinear equation solver.
- 11:
– int64int32nag_int scalar
-
On intermediate exit:
with
,
,
,
or
,
ires contains the value
.
- 12:
– int64int32nag_int scalar
-
On intermediate exit:
indicates what action you must take before re-entering. The possible exit values of
irevcm are
,
,
,
,
,
or
, which should be interpreted as follows:
- , , and
- Indicates that an FCN operation (see Description) is required: must be supplied, where
is located in , for .
For or ,
should be placed in location , for .
For ,
should be placed in location , for .
For ,
should be placed in location , for .
- Indicates that a JAC operation (see Description) is required: the Jacobian matrix must be supplied.
If full matrix linear algebra is being used, then the th element of the Jacobian must be stored in .
If banded matrix linear algebra is being used then the th element of the Jacobian
must be stored in , where and
; here and are the number of subdiagonals and superdiagonals, respectively, in the band.
If sparse matrix linear algebra is being used then
nag_ode_ivp_stiff_sparjac_enq (d02nr) must be called to determine which column of the Jacobian is required and where it should be stored.
[j, iplace] = d02nr(inform);
will return in
j the number of the column of the Jacobian that is required and will set
or
. If
, then the
th element of the Jacobian must be stored in
; otherwise it must be stored in
.
- Indicates that a MONITR operation (see Description) can be performed.
- Indicates that the current step was not successful, due to error test failure or convergence test failure. The only information supplied to you on this return is the current value of the independent variable , located in . No values must be changed before re-entering nag_ode_ivp_stiff_exp_revcom (d02nm); this facility enables you to determine the number of unsuccessful steps.
On final exit:
indicated the user-specified task has been completed or an error has been encountered (see the descriptions for
itask and
ifail).
- 13:
– int64int32nag_int scalar
On final exit:
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
On entry, the integrator detected an illegal input, or that a linear algebra and/or integrator setup function has not been called prior to the call to the integrator. If
, the form of the error will be detailed on the current error message unit (see
nag_file_set_unit_error (x04aa)).
-
-
The maximum number of steps specified has been taken (see the description of optional inputs in the integrator setup functions and the optional input continuation function,
nag_ode_ivp_stiff_contin (d02nz)).
- W
-
With the given values of
rtol and
atol no further progress can be made across the integration range from the current point
t. The components
contain the computed values of the solution at the current point
t.
- W
-
There were repeated error test failures on an attempted step, before completing the requested task, but the integration was successful as far as
t. The problem may have a singularity, or the local error requirements may be inappropriate.
- W
-
There were repeated convergence test failures on an attempted step, before completing the requested task, but the integration was successful as far as
t. This may be caused by an inaccurate Jacobian matrix or one which is incorrectly computed.
- W
-
Some error weight
became zero during the integration (see the description of
itol). Pure relative error control
was requested on a variable (the
th) which has now vanished. The integration was successful as far as
t.
-
-
The FCN operation (see
Description) set the error flag
continually despite repeated attempts by the integrator to avoid this.
-
-
Not used for this integrator.
-
-
A singular Jacobian has been encountered. This error exit is unlikely to be taken when solving explicit ordinary differential equations. You should check the problem formulation and Jacobian calculation.
-
-
An error occurred during Jacobian formulation or back-substitution (a more detailed error description may be directed to the current error message unit, see
nag_file_set_unit_error (x04aa)).
- W
-
The FCN operation (see
Description) signalled the integrator to halt the integration and return by setting
. Integration was successful as far as
t.
- W
-
The MONITR operation (see
Description) set
and so forced a return but the integration was successful as far as
t.
- W
-
The requested task has been completed, but it is estimated that a small change in
rtol and
atol is unlikely to produce any change in the computed solution. (Only applies when you are not operating in one step mode, that is when
or
.)
-
-
The values of
rtol and
atol are so small that
nag_ode_ivp_stiff_exp_revcom (d02nm) is unable to start the integration.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
The accuracy of the numerical solution may be controlled by a careful choice of the arguments
rtol and
atol, and to a much lesser extent by the choice of norm. You are advised to use scalar error control unless the components of the solution are expected to be poorly scaled. For the type of decaying solution typical of many stiff problems, relative error control with a small absolute error threshold will be most appropriate (that is, you are advised to choose
with
small but positive).
Further Comments
The cost of computing a solution depends critically on the size of the differential system and to a lesser extent on the degree of stiffness of the problem; also on the type of linear algebra being used. For further details see
Further Comments of the documents for
nag_ode_ivp_stiff_exp_fulljac (d02nb) (full matrix),
nag_ode_ivp_stiff_exp_bandjac (d02nc) (banded matrix) or
nag_ode_ivp_stiff_exp_sparjac (d02nd) (sparse matrix).
In general, you are advised to choose the backward differentiation formula option (setup function
nag_ode_ivp_stiff_bdf (d02nv)) but if efficiency is of great importance and especially if it is suspected that
has complex eigenvalues near the imaginary axis for some part of the integration, you should try the BLEND option (setup function
nag_ode_ivp_stiff_blend (d02nw)).
Example
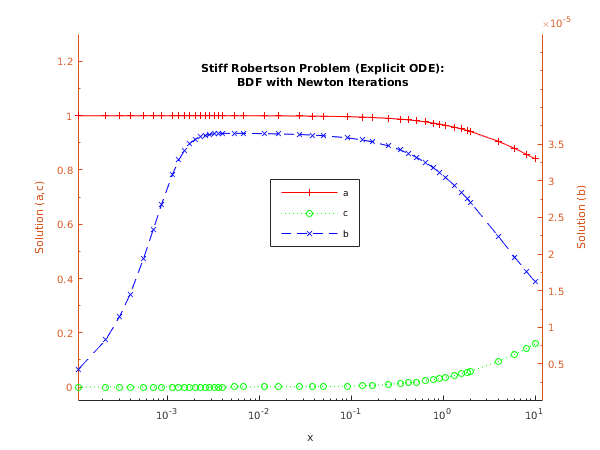
This example solves the well-known stiff Robertson problem
over the range
with initial conditions
and
and with scalar error control (
). The integration proceeds until
is passed, providing
interpolation at intervals of
through a MONITR operation. The integration method used is the BDF method (setup function
nag_ode_ivp_stiff_bdf (d02nv)) with a modified Newton method. The Jacobian is a full matrix, which is specified using the setup function
nag_ode_ivp_stiff_fulljac_setup (d02ns); this Jacobian is to be calculated numerically.
Open in the MATLAB editor:
d02nm_example
function d02nm_example
fprintf('d02nm example results\n\n');
neq = int64(3);
neqmax = neq;
maxord = int64(5);
sdysav = maxord+1;
petzld = false;
tcrit = 0;
hmin = 1.0e-10;
hmax = 10;
h0 = 0;
maxstp = int64(200);
mxhnil = int64(5);
const = zeros(6, 1);
rwork = zeros(50+4*neq, 1);
[const, rwork, ifail] = d02nv( ...
neqmax, sdysav, maxord, 'Newton', petzld, ...
const, tcrit, hmin, hmax, h0, maxstp, ...
mxhnil, 'Average-L2', rwork);
nwkjac = neqmax*(neqmax + 1);
[rwork, ifail] = d02ns( ...
neq, neqmax, 'Numerical', nwkjac, rwork);
njcpvt = int64(1);
wkjac = zeros(nwkjac, 1);
ydot = zeros(neq, 1);
ysave = zeros(neq, sdysav);
inform(1:23) = int64(0);
jacpvt(1) = int64(0);
algequ = zeros(neq, 1);
t = 0;
tout = 10.0;
itask = int64(1);
iout = 1;
xout = 2;
y = [1; 0; 0];
itol = int64(1);
rtol = [1e-04];
atol = [1e-07];
fprintf('\n x y(1) y(2) y(3)\n');
fprintf(' %8.3f %12.4f %12.2e %11.4f\n', t, y);
ncall = 1;
ykeep = y;
tkeep = [t];
irevcm = int64(-999); imon = irevcm; inln = irevcm; ires = irevcm;
itrace = int64(0);
while (irevcm ~= 0)
[t, y, ydot, rwork, inform, ysave, wkjac, jacpvt, imon, inln, ires, ...
irevcm, ifail] = d02nm(...
t, tout, y, ydot, rwork, rtol, atol, itol, ...
inform, ysave, wkjac, jacpvt, imon, inln, ...
ires, irevcm, itask, itrace, 'neq', neq, ...
'sdysav', sdysav, 'nwkjac', nwkjac);
f(1) = -0.04*y(1) + 1.0e4*y(2)*y(3);
f(2) = 0.04*y(1) - 1.0e4*y(2)*y(3) - 3.0e7*y(2)*y(2);
f(3) = 3.0e7*y(2)*y(2);
if (irevcm == 1 || irevcm == 3 )
lrw = 50+2*neq;
rwork(lrw+1:lrw+neq) = f;
elseif (irevcm == 4)
lrw = 50+neq;
rwork(lrw+1:lrw+neq) = f;
elseif (irevcm == 5)
ydot = f;
elseif (irevcm == 9 && imon == 1)
tc = rwork(19);
hlast = rwork(15);
hnext = rwork(16);
nqu = int64(rwork(10));
if tc < 2.0
ncall = ncall + 1;
tkeep(ncall,1) = tc;
ykeep(:,ncall) = y;
end
while (xout <= tc)
lrw = 50+neq;
[sol, ifail] = d02xk(...
xout, neq, ysave, rwork(lrw+1:lrw+neq), ...
tc, nqu, hlast, hnext);
fprintf(' %8.3f %12.4f %12.2e %11.4f\n', xout, sol);
ncall = ncall + 1;
tkeep(ncall) = xout;
ykeep(:,ncall) = sol;
iout = iout + 1;
xout = iout*2;
end
end
end
[hu, h, tcur, tolsf, nst, nre, nje, nqu, nq, niter, imxer, algequ, ifail] ...
= d02ny(...
neq, neqmax, rwork, inform);
fprintf('\nDiagnostic information\n integration status:\n');
fprintf(' last and next step sizes = %8.5f, %8.5f\n',hu, h);
fprintf(' integration stopped at x = %8.5f\n',tcur);
fprintf(' algorithm statistics:\n');
fprintf(' number of time-steps and Newton iterations = %5d %5d\n', ...
nst,niter);
fprintf(' number of residual and jacobian evaluations = %5d %5d\n', ...
nre,nje);
fprintf(' order of method last used and next to use = %5d %5d\n', ...
nqu,nq);
fprintf(' component with largest error = %5d\n',imxer);
fig1 = figure;
display_plot(tkeep, ykeep)
function display_plot(x, y)
hline1 = semilogx(x, y(1,:));
hold on
[haxes, hline2, hline3] = plotyy(x,y(3,:),x,y(2,:), ...
'semilogx','semilogx');
set(haxes(1), 'YLim', [-0.05 1.3]);
set(haxes(1), 'XMinorTick', 'on', 'YMinorTick', 'on');
set(haxes(1), 'YTick', [0.0:0.2:1.2]);
set(haxes(2), 'YLim', [0.0 5e-5]);
set(haxes(2), 'YMinorTick', 'on');
set(haxes(2), 'YTick', [5e-6:5e-6:3.5e-5]);
for iaxis = 1:2
set(haxes(iaxis), 'XLim', [0 12]);
set(haxes(iaxis), 'XTick', [0.0001 0.001 0.01 0.1 1 10]);
end
set(gca, 'box', 'off');
title({'Stiff Robertson Problem (Explicit ODE):', ...
'BDF with Newton Iterations'},'Position',[0.05,1.1]);
xlabel('x');
ylabel(haxes(1),'Solution (a,c)');
ylabel(haxes(2),'Solution (b)');
legend({'a','c','b'},'Position',[0.45,0.45,0.15,0.15]);
set(hline1, 'Marker', '+','Linestyle','-','Color','red');
set(hline2, 'Marker', 'o','Linestyle',':','Color','green');
set(hline3, 'Marker', 'x','Linestyle','--','Color','blue');
hold off
d02nm example results
x y(1) y(2) y(3)
0.000 1.0000 0.00e+00 0.0000
2.000 0.9416 2.70e-05 0.0584
4.000 0.9055 2.24e-05 0.0945
6.000 0.8793 1.96e-05 0.1207
8.000 0.8585 1.77e-05 0.1414
10.000 0.8414 1.62e-05 0.1586
Diagnostic information
integration status:
last and next step sizes = 0.90178, 0.90178
integration stopped at x = 10.76621
algorithm statistics:
number of time-steps and Newton iterations = 55 78
number of residual and jacobian evaluations = 128 16
order of method last used and next to use = 4 4
component with largest error = 3
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015