None.
| On entry, | , |
| or | , |
| or | , |
| or | , |
| or | invalid value for element of the array con, |
| or | , or . |
Open in the MATLAB editor: d02mv_example
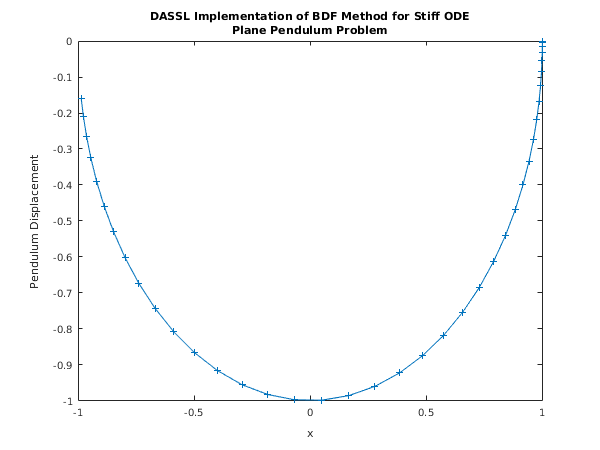
function d02mv_example fprintf('d02mv example results\n\n'); % Initialize setup variables and arrays. neq = int64(6); neqmax = int64(neq); nwkjac = int64(neqmax*(neqmax + 1)); maxord = int64(5); sdysav = int64(maxord+3); maxstp = int64(5000); mxhnil = int64(5); h0 = 0.0; hmax = 0.0; hmin = 1.0e-10; tcrit = pi; const = zeros(3, 1); rwork = zeros(50+4*neqmax, 1); % d02mv is an integration method-specific setup routine to be called prior % to linear algebra setup and integrator routines if the DASSL % implementation of BDF is to be used. [const, rwork, ifail] = d02mv(neqmax, sdysav, maxord, const, tcrit, hmin, ... hmax, h0, maxstp, mxhnil, 'Average-L2', rwork); % d02ns is a setup routine (specifically for full matrix linear algebra) % to be called prior to a routine from sub-chapter d02n-m (e.g. d02ng, % as here). [rwork, ifail] = d02ns(neq, neqmax, 'Analytic', nwkjac, rwork); % Initialize integration variables and arrays wkjac = zeros(nwkjac, 1); ysave = zeros(neq, sdysav); inform(1:23) = int64(0); t = 0; tout = pi; nstep = 38; itol = int64(1); rtol = [1e-03]; atol = [1e-06]; itask = int64(4); itrace = int64(0); lderiv(1:2) = true; y(1:neq) = 0; y(1) = 1; ydot(1:neq) = 0; ydot(1) = y(3) - y(6)*y(1); ydot(2) = y(4) - y(6)*y(2); ydot(3) = -y(5)*y(1); ydot(4) = -y(5)*y(2) - 1.0; ydot(5) = -3*y(4); % Output header and initial results. fprintf(['\nPendulum problem with relative tolerance = %7.1e\n', ... ' and absolute tolerance = %7.1e\n\n'], ... rtol(1), atol(1)); fprintf(' t y1 y2 y3 y4 y5 y6\n'); fprintf(' %6.4f %7.4f %7.4f %7.4f %7.4f %7.4f %7.4f\n', t, y); % Prepare to store results for plotting, then loop over values for the % independent variable. tkeep = zeros(nstep+1,1); ykeep = zeros(neq,nstep+1); tkeep(1) = t; ykeep(:,1) = y; for istep = 1:nstep tout = istep/nstep*pi; [t, tout, y, ydot, rwork, inform, ysave, wkjac, lderiv, ifail] = ... d02ng(t, tout, y, ydot, rwork, rtol, atol, itol, inform, @resid, ... ysave, @jac, wkjac, @monitr, lderiv, itask, itrace); % Store current results for plotting. tkeep(istep+1) = t; ykeep(:,istep+1) = y; end % Output final results. fprintf(' %6.4f %7.4f %7.4f %7.4f %7.4f %7.4f %7.4f\n', t, y); % Plot results. fig1 = figure; display_plot(ykeep(1,:), ykeep(2,:)); function pdj = jac(neq, t, y, ydot, h, d, pdj) % Evaluate the Jacobian. pdj = zeros(neq, neq); hxd = h*d; pdj(1,1) = (1.0 + hxd*y(6)); pdj(1,3) = -hxd; pdj(1,6) = hxd*y(1); pdj(2,2) = (1.0 + hxd*y(6)); pdj(2,4) = -hxd; pdj(2,6) = hxd*y(2); pdj(3,1) = hxd*y(5); pdj(3,3) = 1.0; pdj(3,5) = hxd*y(1); pdj(4,2) = hxd*y(5); pdj(4,4) = 1.0; pdj(4,5) = hxd*y(2); pdj(5,1) = -hxd*y(3); pdj(5,3) = -hxd*y(1); pdj(5,2) = -hxd*y(4); pdj(5,4) = -hxd*y(2); pdj(6,1) = -2*hxd*y(1); pdj(6,2) = -2*hxd*y(2); function [hnext, y, imon, inln, hmin, hmax] = monitr(neq, neqmax, ... t, hlast, hnext, y, ydot, ysave, r, acor, imon, hmin, hmax, nqu) inln = int64(0); function [r, ires] = resid(neq, t, y, ydot, ires) % Evaluate the residue. r = zeros(neq,1); if ires == -1 r(1:4) = -ydot(1:4); r(5:6) = 0.0; else r(1) = y(3) - y(6)*y(1) - ydot(1); r(2) = y(4) - y(6)*y(2) - ydot(2); r(3) = -y(5)*y(1) - ydot(3); r(4) = -y(5)*y(2) - ydot(4) - 1; r(5) = y(1)*y(3) + y(2)*y(4); r(6) = y(1)*y(1) + y(2)*y(2) - 1; end function display_plot(x, y) % Formatting for title and axis labels. % Plot results. plot(x, y, '-+'); % Add title. title({'DASSL Implementation of BDF Method for Stiff ODE',... 'Plane Pendulum Problem'}); % Label the axes. xlabel('x'); ylabel('Pendulum Displacement');
d02mv example results
Pendulum problem with relative tolerance = 1.0e-03
and absolute tolerance = 1.0e-06
t y1 y2 y3 y4 y5 y6
0.0000 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000
3.1416 -0.9872 -0.1597 -0.0902 0.5579 0.4790 -0.0000
