PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_mv_multidimscal_ordinal (g03fc)
Purpose
nag_mv_multidimscal_ordinal (g03fc) performs non-metric (ordinal) multidimensional scaling.
Syntax
[
x,
stress,
dfit,
ifail] = g03fc(
typ,
d,
x,
iter,
iopt, 'n',
n, 'ndim',
ndim)
[
x,
stress,
dfit,
ifail] = nag_mv_multidimscal_ordinal(
typ,
d,
x,
iter,
iopt, 'n',
n, 'ndim',
ndim)
Note: the interface to this routine has changed since earlier releases of the toolbox:
| At Mark 22: |
n was made optional |
Description
For a set of
objects, a distance or dissimilarity matrix
can be calculated such that
is a measure of how ‘far apart’ the objects
and
are. If
variables
have been recorded for each observation this measure may be based on Euclidean distance,
, or some other calculation such as the number of variables for which
. Alternatively, the distances may be the result of a subjective assessment. For a given distance matrix, multidimensional scaling produces a configuration of
points in a chosen number of dimensions,
, such that the distance between the points in some way best matches the distance matrix. For some distance measures, such as Euclidean distance, the size of distance is meaningful, for other measures of distance all that can be said is that one distance is greater or smaller than another. For the former metric scaling can be used, see
nag_mv_multidimscal_metric (g03fa), for the latter, a non-metric scaling is more appropriate.
For non-metric multidimensional scaling, the criterion used to measure the closeness of the fitted distance matrix to the observed distance matrix is known as
stress.
stress is given by,
where
is the Euclidean squared distance between points
and
and
is the fitted distance obtained when
is monotonically regressed on
, that is
is monotonic relative to
and is obtained from
with the smallest number of changes. So
stress is a measure of by how much the set of points preserve the order of the distances in the original distance matrix. Non-metric multidimensional scaling seeks to find the set of points that minimize the
stress.
An alternate measure is squared
stress,
,
in which the distances in
stress are replaced by squared distances.
In order to perform a non-metric scaling, an initial configuration of points is required. This can be obtained from principal coordinate analysis, see
nag_mv_multidimscal_metric (g03fa). Given an initial configuration,
nag_mv_multidimscal_ordinal (g03fc) uses the optimization function
nag_opt_uncon_conjgrd_comp (e04dg) to find the configuration of points that minimizes
stress or
. The function
nag_opt_uncon_conjgrd_comp (e04dg) uses a conjugate gradient algorithm.
nag_mv_multidimscal_ordinal (g03fc) will find an optimum that may only be a local optimum, to be more sure of finding a global optimum several different initial configurations should be used; these can be obtained by randomly perturbing the original initial configuration using functions from
Chapter G05.
References
Chatfield C and Collins A J (1980) Introduction to Multivariate Analysis Chapman and Hall
Krzanowski W J (1990) Principles of Multivariate Analysis Oxford University Press
Parameters
Compulsory Input Parameters
- 1:
– string (length ≥ 1)
-
Indicates whether
stress or
is to be used as the criterion.
- stress is used.
- is used.
Constraint:
or .
- 2:
– double array
-
The lower triangle of the distance matrix
stored packed by rows. That is
must contain
, for
and
. If
is missing then set
; for further comments on missing values see
Further Comments.
- 3:
– double array
-
ldx, the first dimension of the array, must satisfy the constraint
.
The
th row must contain an initial estimate of the coordinates for the
th point, for
. One method of computing these is to use
nag_mv_multidimscal_metric (g03fa).
- 4:
– int64int32nag_int scalar
-
The maximum number of iterations in the optimization process.
- A default value of is used.
- A default value of (the default for nag_opt_uncon_conjgrd_comp (e04dg)) is used.
- 5:
– int64int32nag_int scalar
-
Selects the options, other than the number of iterations, that control the optimization.
- Default values are selected as described in Further Comments. In particular if an accuracy requirement of is selected, see Accuracy.
- The default values are used except that the accuracy is given by where .
- The option setting mechanism of nag_opt_uncon_conjgrd_comp (e04dg) can be used to set all options except Iteration Limit; this option is only recommended if you are an experienced user of NAG optimization functions. For further details see nag_opt_uncon_conjgrd_comp (e04dg).
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the array
d and the first dimension of the array
x. (An error is raised if these dimensions are not equal.)
, the number of objects in the distance matrix.
Constraint:
.
- 2:
– int64int32nag_int scalar
-
Default:
the second dimension of the array
x.
, the number of dimensions used to represent the data.
Constraint:
.
Output Parameters
- 1:
– double array
-
The
th row contains coordinates for the th point, for .
- 2:
– double scalar
-
The value of
stress or
at the final iteration.
- 3:
– double array
-
Auxiliary outputs.
If
, the first
elements contain the distances,
, for the points returned in
x, the second set of
contains the distances
ordered by the input distances,
, the third set of
elements contains the monotonic distances,
, ordered by the input distances,
and the final set of
elements contains fitted monotonic distances,
, for the points in
x. The
corresponding to distances which are input as missing are set to zero.
If , the results are as above except that the squared distances are returned.
Each distance matrix is stored in lower triangular packed form in the same way as the input matrix .
- 4:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
| On entry, | , |
| or | , |
| or | or , |
| or | . |
-
-
| On entry, | all elements of . |
-
-
The optimization has failed to converge in
iter function iterations. Try either increasing the number of iterations using
iter or increasing the value of
, given by
iopt, used to determine convergence. Alternatively try a different starting configuration.
- W
-
The conditions for an acceptable solution have not been met but a lower point could not be found. Try using a larger value of
, given by
iopt.
-
-
The optimization cannot begin from the initial configuration. Try a different set of points.
-
-
The optimization has failed. This error is only likely if
. It corresponds to
,
and
in
nag_opt_uncon_conjgrd_comp (e04dg).
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
After a successful optimization the relative accuracy of
stress should be approximately
, as specified by
iopt.
Further Comments
The optimization function
nag_opt_uncon_conjgrd_comp (e04dg) used by
nag_mv_multidimscal_ordinal (g03fc) has a number of options to control the process. The options for the maximum number of iterations (
Iteration Limit) and accuracy (
Optimality Tolerance) can be controlled by
iter and
iopt respectively. The printing option (
Print Level) is set to
to give no printing. The other option set is to stop the checking of derivatives (
) for efficiency. All other options are left at their default values. If however
is used, only the maximum number of iterations is set. All other options can be controlled by the option setting mechanism of
nag_opt_uncon_conjgrd_comp (e04dg) with the defaults as given by that function.
Missing values in the input distance matrix can be specified by a negative value and providing there are not more than about two thirds of the values missing the algorithm may still work. However the function
nag_mv_multidimscal_metric (g03fa) does not allow for missing values so an alternative method of obtaining an initial set of coordinates is required. It may be possible to estimate the missing values with some form of average and then use
nag_mv_multidimscal_metric (g03fa) to give an initial set of coordinates.
Example
The data, given by
Krzanowski (1990), are dissimilarities between water vole populations in Europe. Initial estimates are provided by the first two principal coordinates computed.
Open in the MATLAB editor:
g03fc_example
function g03fc_example
fprintf('g03fc example results\n\n');
n = int64(14);
d = [0.099 ...
0.033 0.022 ...
0.183 0.114 0.042 ...
0.148 0.224 0.059 0.068 ...
0.198 0.039 0.053 0.085 0.051 ...
0.462 0.266 0.322 0.435 0.268 0.025 ...
0.628 0.442 0.444 0.406 0.240 0.129 0.014 ...
0.113 0.070 0.046 0.047 0.034 0.002 0.106 0.129 ...
0.173 0.119 0.162 0.331 0.177 0.039 0.089 0.237 0.071 ...
0.434 0.419 0.339 0.505 0.469 0.390 0.315 0.349 0.151 0.430 ...
0.762 0.633 0.781 0.700 0.758 0.625 0.469 0.618 0.440 0.538 0.607 ...
0.530 0.389 0.482 0.579 0.597 0.498 0.374 0.562 0.247 0.383 0.387 ...
0.084 ...
0.586 0.435 0.550 0.530 0.552 0.509 0.369 0.471 0.234 0.346 0.456 ...
0.090 0.038];
roots = 'l';
ndim = int64(2);
[x, eval, ifail] = g03fa( ...
roots, n, d, ndim);
typ = 'T';
iter = int64(0);
iopt = int64(0);
[x, stress, dfit, ifail] = g03fc( ...
typ, d, x, iter, iopt);
fprintf('Stress = %13.4e\n\n', stress);
mtitle = 'Co-ordinates';
matrix = 'General';
diag = ' ';
[ifail] = x04ca( ...
matrix,diag,x,mtitle);
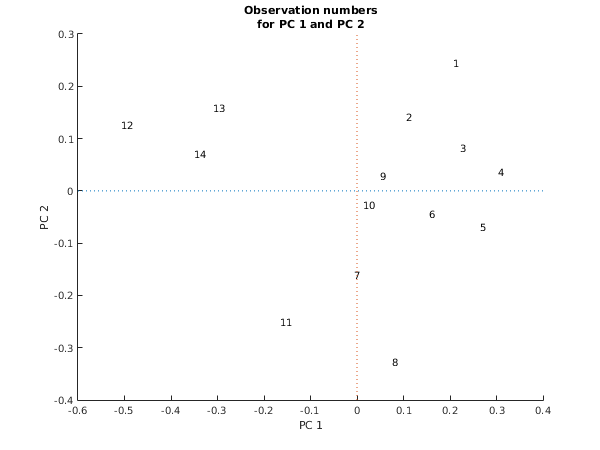
fig1 = figure;
hold on;
xlabel('PC 1');
ylabel('PC 2');
title({'Observation numbers', 'for PC 1 and PC 2'});
axis([-0.6 0.4 -0.4 0.3]);
for j = 1:size(x,1)
ch = sprintf('%d',j);
text(x(j,1),x(j,2),ch);
end
plot([-0.6 0.4], [0 0], ':');
plot([0 0], [-0.4 0.3], ':');
hold off;
g03fc example results
Stress = 1.2557e-01
Co-ordinates
1 2
1 0.2060 0.2438
2 0.1063 0.1418
3 0.2224 0.0817
4 0.3032 0.0355
5 0.2645 -0.0698
6 0.1554 -0.0435
7 -0.0070 -0.1612
8 0.0749 -0.3275
9 0.0488 0.0289
10 0.0124 -0.0267
11 -0.1649 -0.2500
12 -0.5073 0.1267
13 -0.3093 0.1590
14 -0.3498 0.0700
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015