PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_mv_multidimscal_metric (g03fa)
Purpose
nag_mv_multidimscal_metric (g03fa) performs a principal coordinate analysis also known as classical metric scaling.
Syntax
Description
For a set of
objects a distance matrix
can be calculated such that
is a measure of how ‘far apart’ are objects
and
(see
nag_mv_distance_mat (g03ea) for example). Principal coordinate analysis or metric scaling starts with a distance matrix and finds points
in Euclidean space such that those points have the same distance matrix. The aim is to find a small number of dimensions,
, that provide an adequate representation of the distances.
The principal coordinates of the points are computed from the eigenvectors of the matrix where
with denoting the average of over the suffix , etc.. The eigenvectors are then scaled by multiplying by the square root of the value of the corresponding eigenvalue.
Provided that the ordered eigenvalues,
, of the matrix
are all positive,
shows how well the data is represented in
dimensions. The eigenvalues will be non-negative if
is positive semidefinite. This will be true provided
satisfies the inequality:
for all
. If this is not the case the size of the negative eigenvalue reflects the amount of deviation from this condition and the results should be treated cautiously in the presence of large negative eigenvalues. See
Krzanowski (1990) for further discussion.
nag_mv_multidimscal_metric (g03fa) provides the option for all eigenvalues to be computed so that the smallest eigenvalues can be checked.
References
Chatfield C and Collins A J (1980) Introduction to Multivariate Analysis Chapman and Hall
Gower J C (1966) Some distance properties of latent root and vector methods used in multivariate analysis Biometrika 53 325–338
Krzanowski W J (1990) Principles of Multivariate Analysis Oxford University Press
Parameters
Compulsory Input Parameters
- 1:
– string (length ≥ 1)
-
Indicates if all the eigenvalues are to be computed or just the
ndim largest.
- All the eigenvalues are computed.
- Only the largest ndim eigenvalues are computed.
Constraint:
or .
- 2:
– int64int32nag_int scalar
-
, the number of objects in the distance matrix.
Constraint:
.
- 3:
– double array
-
The lower triangle of the distance matrix stored packed by rows. That is must contain for .
Constraint:
, for .
- 4:
– int64int32nag_int scalar
-
, the number of dimensions used to represent the data.
Constraint:
.
Optional Input Parameters
None.
Output Parameters
- 1:
– double array
-
The th row contains coordinates for the th point, .
- 2:
– double array
-
If
,
eval contains the
scaled eigenvalues of the matrix
.
If
,
eval contains the largest
scaled eigenvalues of the matrix
.
In both cases the eigenvalues are divided by the sum of the eigenvalues (that is, the trace of ).
- 3:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
| On entry, | , |
| or | , |
| or | or , |
| or | . |
-
-
| On entry, | for some , , |
| or | all elements of . |
-
-
There are less than
ndim eigenvalues greater than zero. Try a smaller number of dimensions (
ndim) or use non-metric scaling (
nag_mv_multidimscal_ordinal (g03fc)).
-
-
The computation of the eigenvalues or eigenvectors has failed. Seek expert help.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
nag_mv_multidimscal_metric (g03fa) uses
nag_lapack_dsterf (f08jf) or
nag_lapack_dstebz (f08jj) to compute the eigenvalues and
nag_lapack_dstein (f08jk) to compute the eigenvectors. These functions should be consulted for a discussion of the accuracy of the computations involved.
Further Comments
Alternative, non-metric, methods of scaling are provided by
nag_mv_multidimscal_ordinal (g03fc).
The relationship between principal coordinates and principal components, see
nag_mv_multidimscal_ordinal (g03fc), is discussed in
Krzanowski (1990) and
Gower (1966).
Example
The data, given by
Krzanowski (1990), are dissimilarities between water vole populations in Europe. The first two principal coordinates are computed.
Open in the MATLAB editor:
g03fa_example
function g03fa_example
fprintf('g03fa example results\n\n');
roots = 'l';
n = int64(14);
d = [0.099 ...
0.033 0.022 ...
0.183 0.114 0.042 ...
0.148 0.224 0.059 0.068 ...
0.198 0.039 0.053 0.085 0.051 ...
0.462 0.266 0.322 0.435 0.268 0.025 ...
0.628 0.442 0.444 0.406 0.240 0.129 0.014 ...
0.113 0.070 0.046 0.047 0.034 0.002 0.106 0.129 ...
0.173 0.119 0.162 0.331 0.177 0.039 0.089 0.237 0.071 ...
0.434 0.419 0.339 0.505 0.469 0.390 0.315 0.349 0.151 0.430 ...
0.762 0.633 0.781 0.700 0.758 0.625 0.469 0.618 0.440 0.538 0.607 ...
0.530 0.389 0.482 0.579 0.597 0.498 0.374 0.562 0.247 0.383 0.387 ...
0.084 ...
0.586 0.435 0.550 0.530 0.552 0.509 0.369 0.471 0.234 0.346 0.456 ...
0.090 0.038];
ndim = int64(2);
[x, eval, ifail] = g03fa( ...
roots, n, d, ndim);
disp(' Scaled Eigenvalues');
disp(eval(1:ndim)');
mtitle = 'Co-ordinates';
matrix = 'General';
diag = ' ';
[ifail] = x04ca( ...
matrix,diag,x,mtitle);
fig1 = figure;
hold on;
xlabel('PC 1');
ylabel('PC 2');
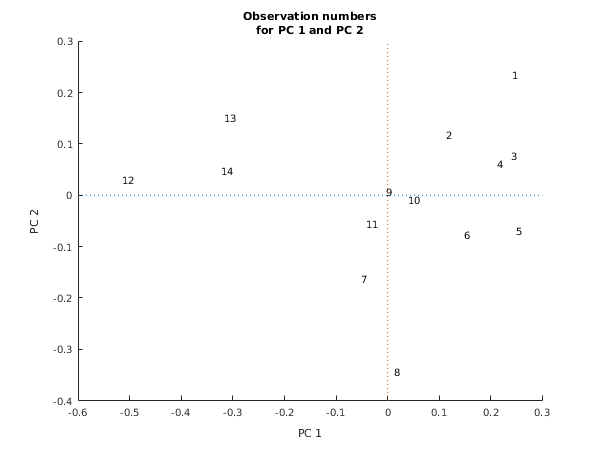
title({'Observation numbers', 'for PC 1 and PC 2'});
axis([-0.6 0.3 -0.4 0.3]);
for j = 1:size(x,1)
ch = sprintf('%d',j);
text(x(j,1),x(j,2),ch);
end
plot([-0.6 0.3], [0 0], ':');
plot([0 0], [-0.4 0.3], ':');
hold off;
g03fa example results
Scaled Eigenvalues
0.7871 0.2808
Co-ordinates
1 2
1 0.2408 0.2337
2 0.1137 0.1168
3 0.2394 0.0760
4 0.2129 0.0605
5 0.2495 -0.0693
6 0.1487 -0.0778
7 -0.0514 -0.1623
8 0.0115 -0.3446
9 -0.0039 0.0059
10 0.0386 -0.0089
11 -0.0421 -0.0566
12 -0.5158 0.0291
13 -0.3180 0.1501
14 -0.3238 0.0475
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015