PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_fit_1dspline_eval (e02bb)
Purpose
nag_fit_1dspline_eval (e02bb) evaluates a cubic spline from its B-spline representation.
Syntax
Description
nag_fit_1dspline_eval (e02bb) evaluates the cubic spline
at a prescribed argument
from its augmented knot set
, for
, (see
nag_fit_1dspline_knots (e02ba)) and from the coefficients
, for
in its B-spline representation
Here
, where
is the number of intervals of the spline, and
denotes the normalized B-spline of degree
defined upon the knots
. The prescribed argument
must satisfy
.
It is assumed that , for , and .
If
is a point at which
knots coincide,
is discontinuous at
; in this case,
s contains the value defined as
is approached from the right.
The method employed is that of evaluation by taking convex combinations due to
de Boor (1972). For further details of the algorithm and its use see
Cox (1972) and
Cox and Hayes (1973).
It is expected that a common use of
nag_fit_1dspline_eval (e02bb) will be the evaluation of the cubic spline approximations produced by
nag_fit_1dspline_knots (e02ba). A generalization of
nag_fit_1dspline_eval (e02bb) which also forms the derivative of
is
nag_fit_1dspline_deriv (e02bc).
nag_fit_1dspline_deriv (e02bc) takes about
longer than
nag_fit_1dspline_eval (e02bb).
References
Cox M G (1972) The numerical evaluation of B-splines J. Inst. Math. Appl. 10 134–149
Cox M G (1978) The numerical evaluation of a spline from its B-spline representation J. Inst. Math. Appl. 21 135–143
Cox M G and Hayes J G (1973) Curve fitting: a guide and suite of algorithms for the non-specialist user NPL Report NAC26 National Physical Laboratory
de Boor C (1972) On calculating with B-splines J. Approx. Theory 6 50–62
Parameters
Compulsory Input Parameters
- 1:
– double array
-
must be set to the value of the th member of the complete set of knots, , for .
Constraint:
the must be in nondecreasing order with .
- 2:
– double array
-
The coefficient
of the B-spline , for . The remaining elements of the array are not referenced.
- 3:
– double scalar
-
The argument at which the cubic spline is to be evaluated.
Constraint:
.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the arrays
lamda,
c. (An error is raised if these dimensions are not equal.)
, where is the number of intervals (one greater than the number of interior knots, i.e., the knots strictly within the range to ) over which the spline is defined.
Constraint:
.
Output Parameters
- 1:
– double scalar
-
The value of the spline, .
- 2:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
The argument
x does not satisfy
.
In this case the value of
s is set arbitrarily to zero.
-
-
, i.e., the number of interior knots is negative.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
The computed value of
has negligible error in most practical situations. Specifically, this value has an
absolute error bounded in modulus by
, where
is the largest in modulus of
and
, and
is an integer such that
. If
and
are all of the same sign, then the computed value of
has a
relative error not exceeding
in modulus. For further details see
Cox (1978).
Further Comments
The time taken is approximately
seconds, where
c is a machine-dependent constant.
Note: the function does not test all the conditions on the knots given in the description of
lamda in
Arguments, since to do this would result in a computation time approximately linear in
instead of
. All the conditions are tested in
nag_fit_1dspline_knots (e02ba), however.
Example
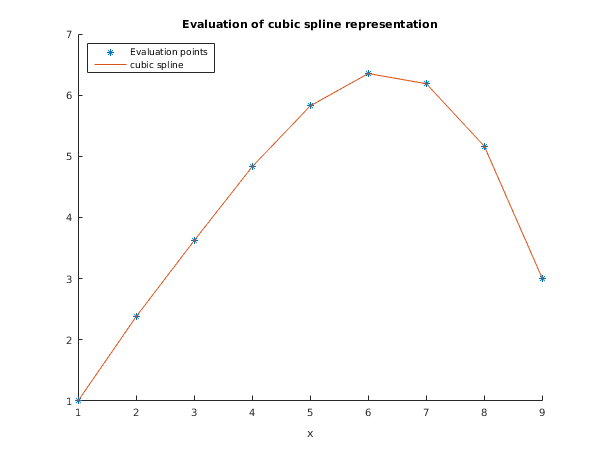
Evaluate at nine equally-spaced points in the interval the cubic spline with (augmented) knots , , , , , , , , , , and normalized cubic B-spline coefficients , , , , , , .
The example program is written in a general form that will enable a cubic spline with intervals, in its normalized cubic B-spline form, to be evaluated at equally-spaced points in the interval . The program is self-starting in that any number of datasets may be supplied.
Open in the MATLAB editor:
e02bb_example
function e02bb_example
fprintf('e02bb example results\n\n');
knots = [3 6 8];
ncap = size(knots,2) + 1;
ncap7 = ncap + 7;
lamda = zeros(ncap7,1);
lamda(1:4) = 1;
lamda(5:7) = knots;
lamda(8:ncap7) = 9;
c = zeros(ncap7,1);
c(1:ncap+3) = [1 2 4 7 6 4 3];
a = lamda(4);
b = lamda(ncap+4);
for x = 1:9;
[s(x), ifail] = e02bb( ...
lamda, c, x);
end
fprintf(' x spline at x\n');
fprintf('%7.2f%14.4f\n',[ [1:9]; s]);
fig1 = figure;
hold on
plot([1:9],s,'*')
plot([1:9],s);
xlabel('x');
title('Evaluation of cubic spline representation');
legend('Evaluation points','cubic spline','Location','NorthWest');
hold off;
e02bb example results
x spline at x
1.00 1.0000
2.00 2.3779
3.00 3.6229
4.00 4.8327
5.00 5.8273
6.00 6.3571
7.00 6.1905
8.00 5.1667
9.00 3.0000
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015