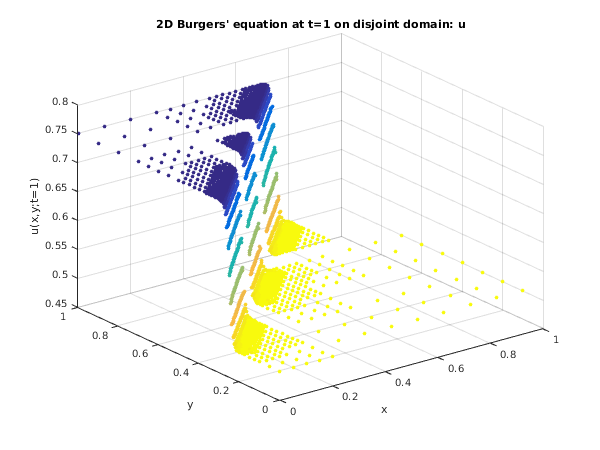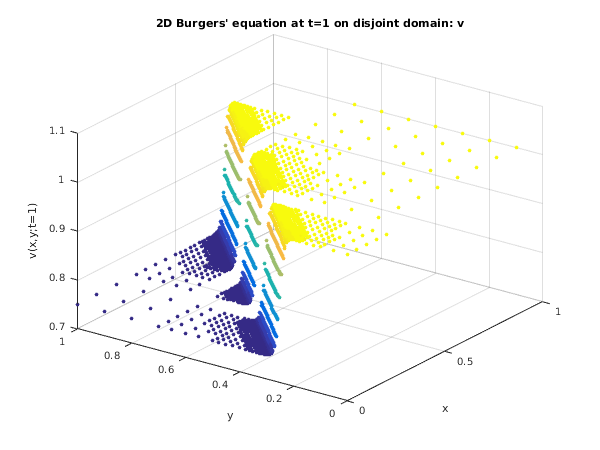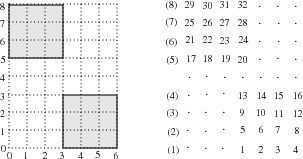
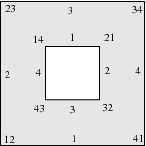
Figure 1
| (1) |
| (2) |

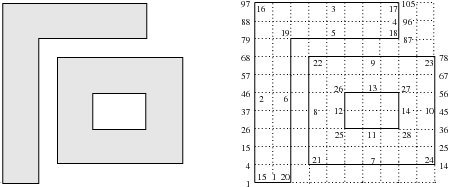
Input Parameters
Output Parameters
Input Parameters
Output Parameters
Input Parameters
Output Parameters
Input Parameters
Output Parameters
Input Parameters
Output Parameters
Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.
| On entry, | , |
| or | , |
| or | tout is too close to ts, |
| or | and , |
| or | , for , |
| or | , |
| or | and , |
| or | and , |
| or | and , |
| or | tols or , |
| or | , |
| or | and , for , or , |
| or | , for some , |
| or | , for some , |
| or | , for some , |
| or | or , |
| or | on initial entry to nag_pde_2d_gen_order2_rectilinear (d03rb). |
| , | |
| or | xmax too close to xmin, |
| or | , |
| or | ymax too close to ymin, |
| or | nx or , |
| or | , |
| or | , |
| or | , |
| or | , |
| or | , |
| or | , |
| or | or , for some , |
| or | , for some , |
| or | or , for some , |
| or | , for some , |
| or | or , for some , |
| or | or , for some , |
| or | , for some , |
| or | , , , , , , , , , , or , for some , |
| or | or , for some . |
| 1. | Initialize the course base grid, an initial solution and an initial time step. | ||||||||||
| 2. | Solve the system of PDEs on the current grid with the current time step. | ||||||||||
| 3. | If the required accuracy in space and the maximum number of grid levels have not yet been reached:
|
||||||||||
| 4. | Update the coarser grid solution using the finer grid values. | ||||||||||
| 5. | Estimate error in time integration. If time error is acceptable advance time level. | ||||||||||
| 6. | Determine new step size then go to with coarse base as current grid. |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Open in the MATLAB editor: d03rb_example
function d03rb_example fprintf('d03rb example results\n\n'); global iout xsol ysol usol vsol inds; ts = 0; twant = [0.25; 1]; dt = [0.001; 1e-07; 0]; tols = 0.1; tolt = 0.05; opti = int64([5;0;0;0]); optr = [1, 1; 1, 1; 1, 1]; rwk = zeros(426000, 1); iwk = zeros(117037, 1, 'int64'); lenlwk = int64(6000); itrace = int64(0); ind = int64(0); inds = int64(0); for iout = 1:2 tout = twant(iout); [ts, dt, rwk, iwk, ind, ifail] = ... d03rb(... ts, tout, dt, tols, tolt, @inidom, @pdedef, ... @bndary, @pdeiv, @monitr, opti, optr, ... rwk, iwk, lenlwk, itrace, ind); fprintf('\nStatistics\n'); fprintf('Time = %8.4f\n', ts); fprintf('Total number of accepted timesteps = %d\n', iwk(1)); fprintf('Total number of rejected timesteps = %d\n', iwk(2)); fprintf('\n T o t a l n u m b e r o f \n'); fprintf(' Residual Jacobian Newton Lin sys\n'); fprintf(' evals evals iters iters\n'); fprintf(' At level \n'); maxlev = opti(1); for j = 1:maxlev if (iwk(j+2) ~= 0) fprintf('%6d %10d %10d %10d %10d\n', j, iwk(j+2), iwk(j+2+maxlev), ... iwk(j+2+2*maxlev), iwk(j+2+3*maxlev) ); end end fprintf('\n M a x i m u m n u m b e r o f\n'); fprintf(' Newton iters Lin sys iters \n'); fprintf(' At level \n'); for j = 1:maxlev if (iwk(j+2) ~= 0) fprintf('%6d%14d%14d\n', j, iwk(j+2+4*maxlev), iwk(j+2+5*maxlev) ); end end end % Plot solutions u and v at t=1.0 fig1 = figure; scatter3(xsol,ysol,usol,15,vsol,'o','fill'); title('2D Burgers'' equation at t=1 on disjoint domain: u'); xlabel('x'); ylabel('y'); zlabel('u(x,y;t=1)'); fig2 = figure; scatter3(xsol,ysol,vsol,15,vsol,'o','fill'); view(-54,32); xlabel('x'); ylabel('y'); zlabel('v(x,y;t=1)'); title('2D Burgers'' equation at t=1 on disjoint domain: v'); function [res] = bndary(npts, npde, t, x, y, u, ut, ux, uy, nbnds, ... nbpts, llbnd, ilbnd, lbnd, res) epsilon = 1e-3; for k = llbnd(1):nbpts i = lbnd(k); a = (-4*x(i)+4*y(i)-t)/(32*epsilon); if (a <= 0) res(i,1) = u(i,1) - (0.75-0.25/(1+exp(a))); res(i,2) = u(i,2) - (0.75+0.25/(1+exp(a))); else res(i,1) = u(i,1) - (0.75-0.25*exp(-a)/(exp(-a)+1)); res(i,2) = u(i,2) - (0.75+0.25*exp(-a)/(exp(-a)+1)); end end function [xmin, xmax, ymin, ymax, nx, ny, npts, nrows, nbnds, nbpts, ... lrow, irow, icol, llbnd, ilbnd, lbnd, ierr] = inidom(maxpts, ierr) nrows = int64(11); npts = int64(105); nbnds = int64(28); nbpts = int64(72); lrow = zeros(nrows, 1, 'int64'); irow = zeros(nrows, 1, 'int64'); icol = zeros(npts, 1, 'int64'); llbnd = zeros(nbnds, 1, 'int64'); ilbnd = zeros(nbnds, 1, 'int64'); lbnd = zeros(nbpts, 1, 'int64'); icold = int64([0,1,2,0,1,2,3,4,5,6,7,8,9,10,0,1,2,3,4,5,6,7,8,9, ... 10,0,1,2,3,4,5,6,7,8,9,10,0,1,2,3,4,5,8,9,10,0,1,2,3,4,5, ... 6,7,8,9,10,0,1,2,3,4,5,6,7,8,9,10,0,1,2,3,4,5,6,7,8,9,10, ... 0,1,2,3,4,5,6,7,8,0,1,2,3,4,5,6,7,8,0,1,2,3,4,5,6,7,8]); ilbndd = int64([1,2,3,4,1,4,1,2,3,4,3,4,1,2,12,23,34,41,14,41,12, ... 23,34,41,43,14,21,32]); irowd = int64([0,1,2,3,4,5,6,7,8,9,10]); lbndd = int64([2,4,15,26,37,46,57,68,79,88,98,99,100,101,102,103,104,96,... 86,85,84,83,82,70,59,48,39,28,17,6,8,9,10,11,12,13,18,... 29,40,49,60,72,73,74,75,76,77,67,56,45,36,25,33,32,42, ... 52,53,43,1,97,105,87,81,3,7,71,78,14,31,51,54,34]); llbndd = int64([1,2,11,18,19,24,31,37,42,48,53,55,56,58,59,60,61,62, ... 63,64,65,66,67,68,69,70,71,72]); lrowd = int64([1,4,15,26,37,46,57,68,79,88,97]); nx = int64(11); ny = int64(11); % check maxpts against rough estimate of npts if (maxpts < nx*ny) ierr = -1; return; end xmin = 0; ymin = 0; xmax = 1; ymax = 1; lrow(1:nrows) = lrowd(1:nrows); irow(1:nrows) = irowd(1:nrows); llbnd(1:nbnds) = llbndd(1:nbnds); ilbnd(1:nbnds) = ilbndd(1:nbnds); lbnd(1:nbpts) = lbndd(1:nbpts); icol(1:npts) = icold(1:npts); function [res] = pdedef(npts, npde, t, x, y, u, ut, ux, uy, uxx, uxy, uyy) res = zeros(npts, npde); epsilon = 1e-3; uxxyy = epsilon*(uxx(1:npts,1:2)+uyy(1:npts,1:2)); uuxuy(1:npts,1) = -u(1:npts,1).*ux(1:npts,1)-u(1:npts,2).*uy(1:npts,1); uuxuy(1:npts,2) = -u(1:npts,1).*ux(1:npts,2)-u(1:npts,2).*uy(1:npts,2); res(1:npts,1:2) = ut(1:npts,1:2)-(uuxuy+uxxyy); function [u] = pdeiv(npts, npde, t, x, y) u = zeros(npts, npde); epsilon = 1e-3; for i = 1:npts a = (-4*x(i)+4*y(i)-t)/(32*epsilon); if (a <= 0) u(i,1) = 0.75 - 0.25/(1+exp(a)); u(i,2) = 0.75 + 0.25/(1+exp(a)); else u(i,1) = 0.75 - 0.25*exp(-a)/(exp(-a)+1); u(i,2) = 0.75 + 0.25*exp(-a)/(exp(-a)+1); end end function [ierr] = ... monitr(npde, t, dt, dtnew, tlast, nlev, xmin, ymin, dxb, dyb, lgrid, ... istruc, lsol, sol, ierr) lenxy=int64(2500); global iout xsol ysol usol vsol inds; if (tlast && iout == 2) for level = int64(1:nlev) ipsol = lsol(level); % Get grid information [npts, x, y, ifail] = ... d03rz(... level, xmin, ymin, dxb, dyb, lgrid, istruc, lenxy); % Get exact solution [uex] = pdeiv(npts, npde, t, x, y); xsol(inds+1:inds+npts) = x(1:npts); ysol(inds+1:inds+npts) = y(1:npts); usol(inds+1:inds+npts) = sol(ipsol+1:ipsol+npts); vsol(inds+1:inds+npts) = sol(ipsol+npts+1:ipsol+npts+npts); inds = inds + npts; end end
d03rb example results
Statistics
Time = 0.2500
Total number of accepted timesteps = 14
Total number of rejected timesteps = 0
T o t a l n u m b e r o f
Residual Jacobian Newton Lin sys
evals evals iters iters
At level
1 196 14 28 14
2 196 14 28 22
3 196 14 28 25
4 196 14 28 31
5 141 10 21 29
M a x i m u m n u m b e r o f
Newton iters Lin sys iters
At level
1 2 1
2 2 1
3 2 1
4 2 2
5 3 2
Statistics
Time = 1.0000
Total number of accepted timesteps = 45
Total number of rejected timesteps = 0
T o t a l n u m b e r o f
Residual Jacobian Newton Lin sys
evals evals iters iters
At level
1 630 45 90 45
2 630 45 90 78
3 630 45 90 87
4 630 45 90 124
5 575 41 83 122
M a x i m u m n u m b e r o f
Newton iters Lin sys iters
At level
1 2 1
2 2 1
3 2 1
4 2 2
5 3 2