PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_pde_2d_gen_order2_rectangle (d03ra)
Purpose
nag_pde_2d_gen_order2_rectangle (d03ra) integrates a system of linear or nonlinear, time-dependent partial differential equations (PDEs) in two space dimensions on a rectangular domain. The method of lines is employed to reduce the PDEs to a system of ordinary differential equations (ODEs) which are solved using a backward differentiation formula (BDF) method. The resulting system of nonlinear equations is solved using a modified Newton method and a Bi-CGSTAB iterative linear solver with ILU preconditioning. Local uniform grid refinement is used to improve the accuracy of the solution.
nag_pde_2d_gen_order2_rectangle (d03ra) originates from the VLUGR2 package (see
Blom and Verwer (1993) and
Blom et al. (1996)).
Syntax
[
ts,
dt,
rwk,
iwk,
ind,
ifail] = d03ra(
ts,
tout,
dt,
xmin,
xmax,
ymin,
ymax,
nx,
ny,
tols,
tolt,
pdedef,
bndary,
pdeiv,
monitr,
opti,
optr,
rwk,
iwk,
itrace,
ind, 'npde',
npde, 'leniwk',
leniwk, 'lenlwk',
lenlwk)
[
ts,
dt,
rwk,
iwk,
ind,
ifail] = nag_pde_2d_gen_order2_rectangle(
ts,
tout,
dt,
xmin,
xmax,
ymin,
ymax,
nx,
ny,
tols,
tolt,
pdedef,
bndary,
pdeiv,
monitr,
opti,
optr,
rwk,
iwk,
itrace,
ind, 'npde',
npde, 'leniwk',
leniwk, 'lenlwk',
lenlwk)
Note: the interface to this routine has changed since earlier releases of the toolbox:
| At Mark 22: |
lenrwk was removed from the interface; lenlwk was made optional |
Description
nag_pde_2d_gen_order2_rectangle (d03ra) integrates the system of PDEs:
for
and
in the rectangular domain
,
, and time interval
, where the vector
is the set of solution values
and
denotes partial differentiation with respect to
, and similarly for
etc.
The functions
must be supplied by you in
pdedef. Similarly the initial values of the functions
must be specified at
in
pdeiv.
Note that whilst complete generality is offered by the master equations
(1),
nag_pde_2d_gen_order2_rectangle (d03ra) is not appropriate for all PDEs. In particular, hyperbolic systems should not be solved using this function. Also, at least one component of
must appear in the system of PDEs.
The boundary conditions must be supplied by you in
bndary in the form
for all
when
or
and for all
when
or
and
The domain is covered by a uniform coarse base grid of size
specified by you, and nested finer uniform subgrids are subsequently created in regions with high spatial activity. The refinement is controlled using a space monitor which is computed from the current solution and a user-supplied space tolerance
tols. A number of optional parameters, e.g., the maximum number of grid levels at any time, and some weighting factors, can be specified in the arrays
opti and
optr. Further details of the refinement strategy can be found in
Further Comments.
The system of PDEs and the boundary conditions are discretized in space on each grid using a standard second-order finite difference scheme (centred on the internal domain and one-sided at the boundaries), and the resulting system of ODEs is integrated in time using a second-order, two-step, implicit BDF method with variable step size. The time integration is controlled using a time monitor computed at each grid level from the current solution and a user-supplied time tolerance
tolt, and some further optional user-specified weighting factors held in
optr (see
Further Comments for details). The time monitor is used to compute a new step size, subject to restrictions on the size of the change between steps, and (optional) user-specified maximum and minimum step sizes held in
dt. The step size is adjusted so that the remaining integration interval is an integer number times
. In this way a solution is obtained at
.
A modified Newton method is used to solve the nonlinear equations arising from the time integration. You may specify (in
opti) the maximum number of Newton iterations to be attempted. A Jacobian matrix is calculated at the beginning of each time step. If the Newton process diverges or the maximum number of iterations is exceeded, a new Jacobian is calculated using the most recent iterates and the Newton process is restarted. If convergence is not achieved after the (optional) user-specified maximum number of new Jacobian evaluations, the time step is retried with
. The linear systems arising from the Newton iteration are solved using a Bi-CGSTAB iterative method, in combination with ILU preconditioning. The maximum number of iterations can be specified by you in
opti.
The solution at all grid levels is stored in the workspace arrays, along with other information needed for a restart (i.e., a continuation call). It is not intended that you extract the solution from these arrays, indeed the necessary information regarding these arrays is not included. The user-supplied monitor
monitr should be used to obtain the solution at particular levels and times.
monitr is called at the end of every time step, with the last step being identified via the input argument
tlast.
Within
pdeiv,
pdedef,
bndary and
monitr the data structure is as follows. Each point on a particular grid is given an index (ranging from
to the total number of points on the grid) and all coordinate or solution information is stored in arrays according to this index, e.g.,
and
contain the
- and
coordinate of point
, and
contains the
th solution component
at point
.
Further details of the underlying algorithm can be found in
Further Comments and in
Blom and Verwer (1993) and
Blom et al. (1996) and the references therein.
References
Adjerid S and Flaherty J E (1988) A local refinement finite element method for two-dimensional parabolic systems SIAM J. Sci. Statist. Comput. 9 792–811
Blom J G, Trompert R A and Verwer J G (1996) Algorithm 758. VLUGR2: A vectorizable adaptive grid solver for PDEs in 2D Trans. Math. Software 22 302–328
Blom J G and Verwer J G (1993) VLUGR2: A vectorized local uniform grid refinement code for PDEs in 2D Report NM-R9306 CWI, Amsterdam
Brown P N, Hindmarsh A C and Petzold L R (1994) Using Krylov methods in the solution of large scale differential-algebraic systems SIAM J. Sci. Statist. Comput. 15 1467–1488
Trompert R A (1993) Local uniform grid refinement and systems of coupled partial differential equations Appl. Numer. Maths 12 331–355
Trompert R A and Verwer J G (1993) Analysis of the implicit Euler local uniform grid refinement method SIAM J. Sci. Comput. 14 259–278
Parameters
Compulsory Input Parameters
- 1:
– double scalar
-
The initial value of the independent variable .
Constraint:
.
- 2:
– double scalar
-
The final value of to which the integration is to be carried out.
- 3:
– double array
-
The initial, minimum and maximum time step sizes respectively.
- Specifies the initial time step size to be used on the first entry, i.e., when . If then the default value is used. On subsequent entries (), the value of is not referenced.
- Specifies the minimum time step size to be attempted by the integrator. If the default value is used.
- Specifies the maximum time step size to be attempted by the integrator. If the default value is used.
Constraints:
- if , ;
- if and ,
and
, where the values of and will have been reset to their default values if zero on entry;
- .
- 4:
– double scalar
- 5:
– double scalar
-
The extents of the rectangular domain in the -direction, i.e., the coordinates of the left and right boundaries respectively.
Constraint:
and
xmax must be sufficiently distinguishable from
xmin for the precision of the machine being used.
- 6:
– double scalar
- 7:
– double scalar
-
The extents of the rectangular domain in the -direction, i.e., the coordinates of the lower and upper boundaries respectively.
Constraint:
and
ymax must be sufficiently distinguishable from
ymin for the precision of the machine being used.
- 8:
– int64int32nag_int scalar
-
The number of grid points in the -direction (including the boundary points).
Constraint:
.
- 9:
– int64int32nag_int scalar
-
The number of grid points in the -direction (including the boundary points).
Constraint:
.
- 10:
– double scalar
-
The space tolerance used in the grid refinement strategy (
in equation
(4)). See
Refinement Strategy.
Constraint:
.
- 11:
– double scalar
-
The time tolerance used to determine the time step size (
in equation
(7)). See
Time Integration .
Constraint:
.
- 12:
– function handle or string containing name of m-file
-
pdedef must evaluate the functions
, for
, in equation
(1) which define the system of PDEs (i.e., the residuals of the resulting ODE system) at all interior points of the domain. Values at points on the boundaries of the domain are ignored and will be overwritten by
bndary.
pdedef is called for each subgrid in turn.
[res] = pdedef(npts, npde, t, x, y, u, ut, ux, uy, uxx, uxy, uyy)
Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of grid points in the current grid.
- 2:
– int64int32nag_int scalar
-
The number of PDEs in the system.
- 3:
– double scalar
-
The current value of the independent variable .
- 4:
– double array
-
contains the coordinate of the th grid point, for .
- 5:
– double array
-
contains the coordinate of the th grid point, for .
- 6:
– double array
-
contains the value of the th PDE component at the th grid point, for and .
- 7:
– double array
-
contains the value of for the th PDE component at the th grid point, for and .
- 8:
– double array
-
contains the value of for the th PDE component at the th grid point, for and .
- 9:
– double array
-
contains the value of for the th PDE component at the th grid point, for and .
- 10:
– double array
-
contains the value of for the th PDE component at the th grid point, for and .
- 11:
– double array
-
contains the value of for the th PDE component at the th grid point, for and .
- 12:
– double array
-
contains the value of for the th PDE component at the th grid point, for and .
Output Parameters
- 1:
– double array
-
must contain the value of , for , at the
th grid point, for , although the residuals at boundary points will be ignored (and overwritten later on) and so they need not be specified here.
- 13:
– function handle or string containing name of m-file
-
bndary must evaluate the functions
, for
, in equation
(2) which define the boundary conditions at all boundary points of the domain. Residuals at interior points must
not be altered by this function.
[res] = bndary(npts, npde, t, x, y, u, ut, ux, uy, nbpts, lbnd, res)
Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of grid points in the current grid.
- 2:
– int64int32nag_int scalar
-
The number of PDEs in the system.
- 3:
– double scalar
-
The current value of the independent variable .
- 4:
– double array
-
contains the coordinate of the th grid point, for .
- 5:
– double array
-
contains the coordinate of the th grid point, for .
- 6:
– double array
-
contains the value of the th PDE component at the th grid point, for and .
- 7:
– double array
-
contains the value of for the th PDE component at the th grid point, for and .
- 8:
– double array
-
contains the value of for the th PDE component at the th grid point, for and .
- 9:
– double array
-
contains the value of for the th PDE component at the th grid point, for and .
- 10:
– int64int32nag_int scalar
-
The number of boundary points in the grid.
- 11:
– int64int32nag_int array
-
contains the grid index for the th boundary point, for . Hence the th boundary point has coordinates and , and the corresponding solution values are , etc.
- 12:
– double array
-
contains the value of
, for
, at the
th grid point, for
, as returned by
pdedef. The residuals at the boundary points will be overwritten and so need not have been set by
pdedef.
Output Parameters
- 1:
– double array
-
must contain the value of
, for
, at the
th boundary point, for
.
Note: elements of
res corresponding to interior points must
not be altered.
- 14:
– function handle or string containing name of m-file
-
pdeiv must specify the initial values of the PDE components
at all points in the grid.
pdeiv is not referenced if, on entry,
.
[u] = pdeiv(npts, npde, t, x, y)
Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of grid points in the grid.
- 2:
– int64int32nag_int scalar
-
The number of PDEs in the system.
- 3:
– double scalar
-
The (initial) value of the independent variable .
- 4:
– double array
-
contains the coordinate of the th grid point, for .
- 5:
– double array
-
contains the coordinate of the th grid point, for .
Output Parameters
- 1:
– double array
-
must contain the value of the th PDE component at the th grid point, for and .
- 15:
– function handle or string containing name of m-file
-
monitr is called by
nag_pde_2d_gen_order2_rectangle (d03ra) at the end of every successful time step, and may be used to examine or print the solution or perform other tasks such as error calculations, particularly at the final time step, indicated by the argument
tlast. The input arguments contain information about the grid and solution at all grid levels used.
monitr can also be used to force an immediate tidy termination of the solution process and return to the calling program.
[ierr] = monitr(npde, t, dt, dtnew, tlast, nlev, ngpts, xpts, ypts, lsol, sol, ierr)
Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of PDEs in the system.
- 2:
– double scalar
-
The current value of the independent variable , i.e., the time at the end of the integration step just completed.
- 3:
– double scalar
-
The current time step size , i.e., the time step size used for the integration step just completed.
- 4:
– double scalar
-
The step size that will be used for the next time step.
- 5:
– logical scalar
-
Indicates if intermediate or final time step.
for an intermediate step,
for the last call to
monitr before returning to your program.
- 6:
– int64int32nag_int scalar
-
The number of grid levels used at time
t.
- 7:
– int64int32nag_int array
-
contains the number of grid points at level , for .
- 8:
– double array
-
Contains the
coordinates of the grid points in each level in turn, i.e.,
, for
and
.
So for level , , where , for and .
- 9:
– double array
-
Contains the
coordinates of the grid points in each level in turn, i.e.,
, for
and
.
So for level , , where , for and .
- 10:
– int64int32nag_int array
-
contains the pointer to the solution in
sol at grid level
and time
t. (
actually contains the array index immediately preceding the start of the solution in
sol.)
- 11:
– double array
Default:
Contains the solution
at time
t for each grid level
in turn, positioned according to
lsol, i.e., for level
,
, for
,
and
.
- 12:
– int64int32nag_int scalar
-
Will be set to .
Output Parameters
- 1:
– int64int32nag_int scalar
-
Should be set to
to force a tidy termination and an immediate return to the calling program with
.
ierr should remain unchanged otherwise.
- 16:
– int64int32nag_int array
-
May be set to control various options available in the integrator.
- All the default options are employed.
- The default value of
, for , can be obtained by setting .
- Specifies the maximum number of grid levels allowed (including the base grid). . The default value is .
- Specifies the maximum number of Jacobian evaluations allowed during each nonlinear equations solution. . The default value is .
- Specifies the maximum number of Newton iterations in each nonlinear equations solution. . The default value is .
- Specifies the maximum number of iterations in each linear equations solution. . The default value is .
Constraint:
and if , , for .
- 17:
– double array
-
May be used to specify the optional vectors
,
and
in the space and time monitors (see
Further Comments).
If an optional vector is not required then all its components should be set to .
, for
, specifies
, the approximate maximum absolute value of the
th component of
, as used in
(4) and
(7).
, for
.
, for
, specifies
, the weighting factors used in the space monitor (see
(4)) to indicate the relative importance of the
th component of
on the space monitor.
, for
.
, for
, specifies
, the weighting factors used in the time monitor (see
(6)) to indicate the relative importance of the
th component of
on the time monitor.
, for
.
Constraints:
- , for ;
- , for and .
- 18:
– double array
lenrwk, the dimension of the array, must satisfy the constraint
(the required size for the initial grid).
The required value of
lenrwk cannot be determined exactly in advance, but a suggested value is
where
if
and
otherwise, and
is the expected maximum number of grid points at any one level. If during the execution the supplied value is found to be too small then the function returns with
and an estimated required size is printed on the current error message unit (see
nag_file_set_unit_error (x04aa)).
Constraint:
(the required size for the initial grid).
- 19:
– int64int32nag_int array
-
If
,
iwk need not be set. Otherwise
iwk must remain unchanged from a previous call to
nag_pde_2d_gen_order2_rectangle (d03ra).
- 20:
– int64int32nag_int scalar
-
The level of trace information required from
nag_pde_2d_gen_order2_rectangle (d03ra).
itrace may take the value
,
,
,
or
.
- No output is generated.
- Only warning messages are printed.
- Output from the underlying solver is printed on the current advisory message unit (see nag_file_set_unit_advisory (x04ab)). This output contains details of the time integration, the nonlinear iteration and the linear solver.
If , then is assumed and similarly if , then is assumed.
The advisory messages are given in greater detail as
itrace increases. Setting
allows you to monitor the progress of the integration without possibly excessive information.
- 21:
– int64int32nag_int scalar
-
Must be set to
or
, alternatively
or
.
- Starts the integration in time. pdedef is assumed to be serial.
- Continues the integration after an earlier exit from the function. In this case, only the following parameters may be reset between calls to nag_pde_2d_gen_order2_rectangle (d03ra): tout, dt, tols, tolt, opti, optr, itrace and ifail. pdedef is assumed to be serial.
-
Equivalent to . This option is included only for compatibility with other NAG library products.
-
Equivalent to . This option is included only for compatibility with other NAG library products.
Constraint:
or .
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the array
optr.
The number of PDEs in the system.
Constraint:
.
- 2:
– int64int32nag_int scalar
-
Default:
the dimension of the array
iwk.
The dimension of the array
iwk.
The required value of
leniwk cannot be determined exactly in advance, but a suggested value is
where
is the expected maximum number of grid points at any one level and
if
and
otherwise. If during the execution the supplied value is found to be too small then the function returns with
and an estimated required size is printed on the current error message unit (see
nag_file_set_unit_error (x04aa)).
Constraint:
(the required size for the initial grid).
- 3:
– int64int32nag_int scalar
Default:
The dimension of the array
lwk.
The required value of
lenlwk cannot be determined exactly in advanced, but a suggested value is
where
is the expected maximum number of grid points at any one level. If during the execution the supplied value is found to be too small then the function returns with
and an estimated required size is printed on the current error message unit (see
nag_file_set_unit_error (x04aa)).
Constraint:
(the required size for the initial grid).
Output Parameters
- 1:
– double scalar
-
The value of which has been reached. Normally .
- 2:
– double array
-
contains the time step size for the next time step. and are unchanged or set to their default values if zero on entry.
- 3:
– double array
(the required size for the initial grid).
Communication array, used to store information between calls to nag_pde_2d_gen_order2_rectangle (d03ra).
- 4:
– int64int32nag_int array
-
The following components of the array
iwk concern the efficiency of the integration. Here,
is the maximum number of grid levels allowed (
if
and
otherwise), and
is a grid level taking the values
, where
is the number of levels used.
- Contains the number of steps taken in time.
- Contains the number of rejected time steps.
- Contains the total number of residual evaluations performed (i.e., the number of times pdedef was called) at grid level .
- Contains the total number of Jacobian evaluations performed at grid level .
- Contains the total number of Newton iterations performed at grid level .
- Contains the total number of linear solver iterations performed at grid level .
- Contains the maximum number of Newton iterations performed at any one time step at grid level .
- Contains the maximum number of linear solver iterations performed at any one time step at grid level .
Note: the total and maximum numbers are cumulative over all calls to nag_pde_2d_gen_order2_rectangle (d03ra). If the specified maximum number of Newton or linear solver iterations is exceeded at any stage, then the maximums above are set to the specified maximum plus one.
- 5:
– int64int32nag_int scalar
-
, if
ind on input was
or
, or
, if
ind on input was
or
.
- 6:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
| On entry, | , |
| or | , |
| or | tout is too close to ts, |
| or | and , |
| or | , for , |
| or | , |
| or | and , |
| or | and , |
| or | and or , |
| or | , |
| or | xmax too close to xmin, |
| or | , |
| or | ymax too close to ymin, |
| or | nx or , |
| or | tols or , |
| or | , |
| or | and , for , or , |
| or | , for some , |
| or | , for some , |
| or | , for some , |
| or | lenrwk, leniwk or lenlwk too small for initial grid level, |
| or | or , |
| or | on initial entry to nag_pde_2d_gen_order2_rectangle (d03ra). |
-
-
The time step size to be attempted is less than the specified minimum size. This may occur following time step failures and subsequent step size reductions caused by one or more of the following:
- the requested accuracy could not be achieved, i.e., tolt is too small,
- the maximum number of linear solver iterations, Newton iterations or Jacobian evaluations is too small,
- ILU decomposition of the Jacobian matrix could not be performed, possibly due to singularity of the Jacobian.
Setting
itrace to a higher value may provide further information.
In the latter two cases you are advised to check their problem formulation in
pdedef and/or
bndary, and the initial values in
pdeiv if appropriate.
-
-
One or more of the workspace arrays is too small for the required number of grid points. An estimate of the required sizes for the current stage is output, but more space may be required at a later stage.
- W
-
ierr was set to
in
monitr, forcing control to be passed back to calling program. Integration was successful as far as
.
- W
-
The integration has been completed but the maximum number of levels specified in
was insufficient at one or more time steps, meaning that the requested space accuracy could not be achieved. To avoid this warning either increase the value of
or decrease the value of
tols.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
There are three sources of error in the algorithm: space and time discretization, and interpolation (linear) between grid levels. The space and time discretization errors are controlled separately using the arguments
tols and
tolt described in the following section, and you should test the effects of varying these arguments. Interpolation errors are generally implicitly controlled by the refinement criterion since in areas where interpolation errors are potentially large, the space monitor will also be large. It can be shown that the global spatial accuracy is comparable to that which would be obtained on a uniform grid of the finest grid size. A full error analysis can be found in
Trompert and Verwer (1993).
Further Comments
Algorithm Outline
The local uniform grid refinement method is summarised as follows:
| 1. |
Initialize the course base grid, an initial solution and an initial time step. |
| 2. |
Solve the system of PDEs on the current grid with the current time step. |
| 3. |
If the required accuracy in space and the maximum number of grid levels have not yet been reached:
| (a) |
Determine new finer grid at forward time level. |
| (b) |
Get solution values at previous time level(s) on new grid. |
| (c) |
Interpolate internal boundary values from old grid at forward time. |
| (d) |
Get initial values for the Newton process at forward time. |
| (e) |
Go to . |
|
| 4. |
Update the coarser grid solution using the finer grid values. |
| 5. |
Estimate error in time integration. If time error is acceptable advance time level. |
| 6. |
Determine new step size then go to with coarse base as current grid. |
Refinement Strategy
For each grid point
a space monitor
is determined by
where
and
are the grid widths in the
and
directions; and
,
are the
and
coordinates at grid point
. The argument
is obtained from
where
is the user-supplied space tolerance;
is a weighting factor for the relative importance of the
th PDE component on the space monitor; and
is the approximate maximum absolute value of the
th component. A value for
must be supplied by you. Values for
and
must also be supplied but may be set to the value
if little information about the solution is known.
A new level of refinement is created if
depending on the grid level at the previous step in order to avoid fluctuations in the number of grid levels between time steps. If
(5) is satisfied then all grid points for which
are flagged and surrounding cells are quartered in size.
No derefinement takes place as such, since at each time step the solution on the base grid is computed first and new finer grids are then created based on the new solution. Hence derefinement occurs implicitly. See
Algorithm Outline.
Time Integration
The time integration is controlled using a time monitor calculated at each level
up to the maximum level used, given by
where
is the total number of points on grid level
;
;
is the current time step;
is the time derivative of
which is approximated by first-order finite differences;
is the time equivalent of the space weighting factor
; and
is given by
where
is as before, and
is the user-specified time tolerance.
An integration step is rejected and retried at all levels if
Example
For this function two examples are presented, with a main program and two example problems given in Example 1 (EX1) and Example 2 (EX2).
Example 1 (EX1)
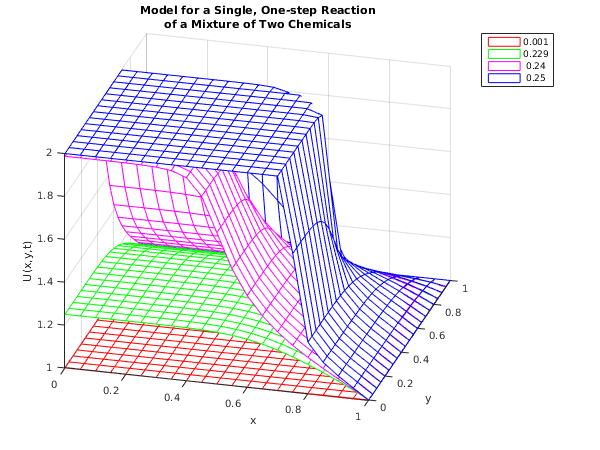
This example stems from combustion theory and is a model for a single, one-step reaction of a mixture of two chemicals (see
Adjerid and Flaherty (1988)). The PDE for the temperature of the mixture
is
for
and
, with initial conditions
for
, and boundary conditions
The heat release argument
, the Damkohler number
, the activation energy
, the reaction rate
, and the diffusion argument
.
For small times the temperature gradually increases in a circular region about the origin, and at about ‘ignition’ occurs causing the temperature to suddenly jump from near unity to , and a reaction front forms and propagates outwards, becoming steeper. Thus during the solution, just one grid level is used up to the ignition point, then two levels, and then three as the reaction front steepens.
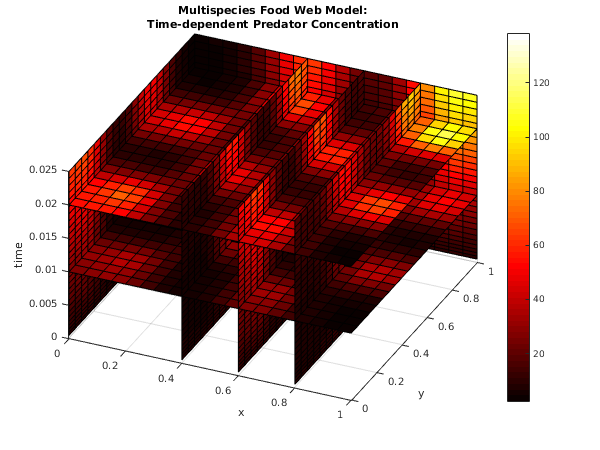
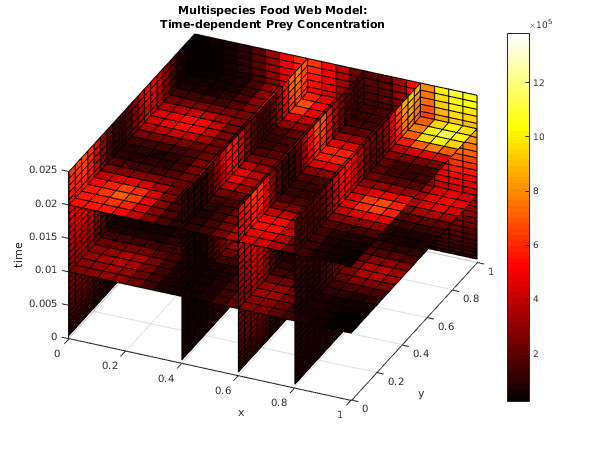
Example 2 (EX2)
This example is taken from a multispecies food web model, in which predator-prey relationships in a spatial domain are simulated (see
Brown et al. (1994)). In this example there is just one species each of prey and predator, and the two PDEs for the concentrations
and
of the prey and the predator respectively are
with
where
and
, and
.
The initial conditions are taken to be simple peaked functions which satisfy the boundary conditions and very nearly satisfy the PDEs:
and the boundary conditions are of Neumann type, i.e., zero normal derivatives everywhere.
During the solution a number of peaks and troughs develop across the domain, and so the number of levels required increases with time. Since the solution varies rapidly in space across the whole of the domain, refinement at intermediate levels tends to occur at all points of the domain.
Open in the MATLAB editor:
d03ra_example
function d03ra_example
fprintf('d03ra example results\n\n');
global ssav1 ssav2;
global xsav ysav tsav;
ex1;
fig1 = figure;
ex1_plot;
ex2;
fig2 = figure;
ex2_plot(1);
fig3 = figure;
ex2_plot(2);
function ex1
global heat_release activ_energy diffusion damkohler;
global iout isav;
mxlev = 3;
npde = 1;
npts = 2000;
xmin = 0; xmax = 1;
ymin = 0; ymax = 1;
tols = 0.5;
tolt = 0.01;
nx = int64(21);
ny = nx;
reaction_rate = 5;
activ_energy = 20;
heat_release = 1;
diffusion = 0.1;
damkohler = reaction_rate*exp(activ_energy)/(heat_release*activ_energy);
leniwk = npts*(14 + 5*mxlev) + 7*mxlev + 2;
lenlwk = npts + 1;
lenrwk = npts*npde*(5*mxlev + 18*npde + 9) + 2*npts;
leniwk = 2*leniwk;
lenlwk = int64(2*lenlwk);
lenrwk = 2*lenrwk;
rwk = zeros(lenrwk, 1);
iwk = zeros(leniwk, 1, 'int64');
ind = int64(0);
itrace = int64(0);
ts = 0;
dt = [0.1e-2; 0.0; 0.0];
twant = [0.24; 0.25];
opti = zeros(4, 1, 'int64');
optr = ones(3, npde);
isav = 1;
warning('Off');
fprintf('Example 1\n==========\n\n');
for iout = 1:2
tout = twant(iout);
[ts, dt, rwk, iwk, ind, ifail] = ...
d03ra( ...
ts, tout, dt, xmin, xmax, ymin, ymax, nx, ny, tols, tolt, ...
@ex1_pdedef, @ex1_bndary, @ex1_pdeiv, @ex1_monitr, opti, ...
optr, rwk, iwk, itrace, ind, 'lenlwk', lenlwk);
fprintf('\nTime =%8.4f \n', ts);
fprintf('Total number of accepted timesteps %5d \n', iwk(1));
fprintf('Total number of rejected timesteps %5d \n', iwk(2));
fprintf('\n Total (max) number of\n');
fprintf(' Residual Jacobian Newton Lin sys\n');
fprintf(' evals evals iters iters\n');
fprintf('At level\n');
maxlev = 3;
for j = 1:maxlev
if iwk(j+2) ~= 0
evals = iwk(j+2:maxlev:j+2+5*maxlev);
fprintf('%8d%10d%10d%6d(%2d)%6d(%2d)\n', j, evals);
end;
end;
end
function [res] = ex1_pdedef(npts, npde, t, x, y, u, ut, ux, uy, uxx, uxy, uyy)
global heat_release activ_energy diffusion damkohler;
res = zeros(npts, npde);
for i = 1:npts
e = exp(-activ_energy/u(i,1));
res(i,1) = ut(i,1) - diffusion*(uxx(i,1) + uyy(i,1)) - ...
damkohler*(1.0 + heat_release - u(i,1))*e;
end
function [u] = ex1_pdeiv(npts, npde, t, x, y)
u = ones(npts, npde);
function [res] = ex1_bndary(npts, npde, t, x, y, u, ut, ux, uy, ...
nbpts, lbnd, res)
tol = 10*x02aj();
for i = 1:nbpts
j = lbnd(i);
if (abs(x(j)) <= tol)
res(j,1) = ux(j,1);
elseif (abs(x(j)-1) <= tol)
res(j,1) = u(j,1) - 1;
elseif (abs(y(j)) <= tol)
res(j,1) = uy(j,1);
elseif (abs(y(j)-1) <= tol)
res(j,1) = u(j,1) - 1;
end
end
function [ierr] = ex1_monitr(npde, t, dt, dtnew, tlast, nlev, ...
ngpts, xpts, ypts, lsol, sol, ierr)
times = [0.001; 0.228; 0.240; 0.25];
global iout isav;
global xsav ysav ssav1 tsav;
if (t < times(isav))
return;
end
fprintf('Saving set %d at time = %f\n', isav, t);
level = 1;
npts = ngpts(level);
ipsol = lsol(level);
nside = round(sqrt(double(npts)));
if isav == 1
nsav = length(times);
xsav = zeros(nside, 1);
ysav = zeros(nside, 1);
ssav1 = zeros(nside, nside, nsav);
tsav = zeros(nsav, 1);
end
tsav(isav) = t;
for i = 1:nside
for j = 1:nside
k = (i-1)*nside + j;
xsav(j) = xpts(k);
ysav(i) = ypts(k);
ssav1(j, i, isav) = sol(ipsol+k);
end
end
if ~(tlast && iout == 2)
isav = isav+1;
end
function ex1_plot
global xsav ysav ssav1 tsav isav;
colours = [[1 0 0]; [0 1 0]; [1 0 1]; [0 0 1]; [0 1 1]; [2 1 0]; [2 0 1];
[1 0 2]; [1 2 0]; [0 1 2]; [0 2 1]; [3 2 1]; [2 3 1]; [2 1 3];
[3 1 2]; [1 3 2]; [1 2 3]; [0.3 2 1]; [2 0.3 1]; [2 1 0.3];
[0.3 1 2]; [1 0.3 2]; [1 2 0.3]; [0.3 0.2 1]; [0.2 0.3 1];
[0.2 1 0.3]; [0.3 1 0.2]; [1 0.3 0.2]; [1 0.2 0.3]];
h = zeros(isav,1);
if (length(colours(:,1)) < isav)
fprintf(['Not enough colours allocated in example1_plot: ', ...
'%d needed\n'], isav);
end
for i = 1:isav
h(i) = mesh(xsav, ysav, ssav1(:,:,i));
hold on;
set(h(i), 'EdgeColor', colours(i,:));
end
hold off;
xlabel('x');
ylabel('y');
zlabel('U(x,y,t)');
title({'Model for a Single, One-step Reaction', ...
'of a Mixture of Two Chemicals'});
hleg = legend(h, num2str(tsav(1:isav)));
view(15, 30);
function ex2
global alpha beta;
global iout icount;
npde = int64(2);
npts = int64(4000);
xmin = 0; xmax = 1;
ymin = 0; ymax = 1;
tols = 0.075;
tolt = 0.1;
nx = int64(21);
ny = int64(21);
alpha = 50.0;
beta = 300.0;
maxlev = 4;
leniwk = npts*(14 + 5*maxlev) + 7*maxlev + 2;
lenlwk = npts + 1;
lenrwk = npts*npde*(5*maxlev + 18*npde + 9) + 2*npts;
leniwk = 2*leniwk;
lenlwk = int64(3*lenlwk);
lenrwk = 3*lenrwk;
rwk = zeros(lenrwk, 1);
iwk = zeros(leniwk, 1, 'int64');
ind = int64(0);
itrace = int64(0);
ts = 0;
dt = [0.5e-3; 1.0e-6; 0.0];
twant = [0.01; 0.025];
opti = zeros(4, 1, 'int64');
opti(1) = 4;
optr = ones(3, npde);
optr(1,1) = 250;
optr(1,2) = 1.5e+6;
icount = 0;
fprintf('\n\nExample 2\n=========\n\n');
for iout = 1:2
tout = twant(iout);
[ts, dt, rwk, iwk, ind, ifail] = ...
d03ra( ...
ts, tout, dt, xmin, xmax, ymin, ymax, nx, ny, tols, tolt, ...
@ex2_pdedef, @ex2_bndary, @ex2_pdeiv, @ex2_monitr, opti, optr, ...
rwk, iwk, itrace, ind, 'lenlwk', lenlwk);
fprintf('\nTime =%8.4f \n', ts);
fprintf('Total number of accepted timesteps %5d \n', iwk(1));
fprintf('Total number of rejected timesteps %5d \n', iwk(2));
fprintf('\n Total (max) number of\n');
fprintf(' Residual Jacobian Newton Lin sys\n');
fprintf(' evals evals iters iters\n');
fprintf('At level\n');
for j = 1:maxlev
if iwk(j+2) ~= 0
evals = iwk(j+2:maxlev:j+2+5*maxlev);
fprintf('%8d%10d%10d%6d(%2d)%6d(%2d)\n', j, evals);
end;
end;
end
function [res] = ex2_pdedef(npts, npde, t, x, y, u, ut, ux, uy, ...
uxx, uxy, uyy)
global alpha beta;
fp = 4*pi;
res = zeros(npts, npde);
for i = 1:npts
b1 = 1 + alpha*x(i)*y(i) + beta*sin(fp*x(i))*sin(fp*y(i));
res(i,1) = ut(i,1) - uxx(i,1) - uyy(i,1) - ...
u(i,1)*(b1 - u(i,1) - 0.5e-6*u(i,2));
res(i,2) = -0.05*(uxx(i,2) + uyy(i,2)) - ...
u(i,2)*(-b1 + 1.0e4*u(i,1) - u(i,2));
end
function [u] = ex2_pdeiv(npts, npde, t, x, y)
global alpha beta;
fp = 4*pi;
u = zeros(npts, npde);
for i = 1:npts
u(i,1) = 10 + (16*x(i)*(1 - x(i))*y(i)*(1 - y(i)))^2;
u(i,2) = -1 - alpha*x(i)*y(i) - beta*sin(fp*x(i))*sin(fp*y(i)) + ...
1.0e4*u(i,1);
end
function [res] = ex2_bndary(npts, npde, t, x, y, u, ut, ux, uy, ...
nbpts, lbnd, res)
tol = 10*x02aj;
for i = 1:nbpts
j = lbnd(i);
if (abs(x(j)) <= tol || abs(x(j)-1) <= tol)
res(j,1) = ux(j,1);
res(j,2) = ux(j,2);
elseif (abs(y(j)) <= tol || abs(y(j)-1) <= tol)
res(j,1) = uy(j,1);
res(j,2) = uy(j,2);
end
end
function [ierr] = ex2_monitr(npde, t, dt, dtnew, tlast, nlev, ...
ngpts, xpts, ypts, lsol, sol, ierr)
global iout icount;
global xsav ysav ssav2 tsav isav;
size(xpts);
size(ypts);
icount = icount+1;
isav = icount;
level = 1;
npts = ngpts(level);
ipsol = lsol(level);
nside = round(sqrt(double(npts)));
tsav(isav) = t;
if (icount==1)
xsav(1:nside) = xpts(1:nside);
ysav(1:nside) = ypts(1:nside:nside^2);
end
s1 = reshape(sol(ipsol+1:ipsol+nside^2),[nside,nside]);
s2 = reshape(sol(ipsol+npts+1:ipsol+npts+nside^2),[nside,nside]);
ssav2(:,:,isav,1) = s1';
ssav2(:,:,isav,2) = s2';
function ex2_plot(id)
global xsav ysav ssav2 tsav isav;
if (id ~= 1 && id ~= 2)
fprintf('Illegal value for array identifier in plot: %d\n', id);
return;
end
v = ssav2(:,:,:,id);
slice(xsav, ysav, tsav, v ,[0,0.4,0.6,0.8],[1],[0.01,0.02]);
colormap hot;
colorbar;
xlabel('x');
ylabel('y');
zlabel('time');
if (id == 1)
title({'Multispecies Food Web Model:', ...
'Time-dependent Predator Concentration'});
else
title({'Multispecies Food Web Model:', ...
'Time-dependent Prey Concentration'});
end
view(24,42);
d03ra example results
Example 1
==========
Saving set 1 at time = 0.001000
Saving set 2 at time = 0.228996
Saving set 3 at time = 0.240000
Time = 0.2400
Total number of accepted timesteps 75
Total number of rejected timesteps 0
Total (max) number of
Residual Jacobian Newton Lin sys
evals evals iters iters
At level
1 600 75 150(159) 2( 2)
Saving set 4 at time = 0.250000
Time = 0.2500
Total number of accepted timesteps 180
Total number of rejected timesteps 1
Total (max) number of
Residual Jacobian Newton Lin sys
evals evals iters iters
At level
1 1468 181 382(391) 4( 2)
2 662 82 170(170) 4( 1)
3 177 22 45(45) 3( 1)
Example 2
=========
Time = 0.0100
Total number of accepted timesteps 14
Total number of rejected timesteps 0
Total (max) number of
Residual Jacobian Newton Lin sys
evals evals iters iters
At level
1 196 14 28(39) 2( 2)
2 84 6 12(19) 2( 3)
Time = 0.0250
Total number of accepted timesteps 29
Total number of rejected timesteps 0
Total (max) number of
Residual Jacobian Newton Lin sys
evals evals iters iters
At level
1 406 29 58(84) 2( 2)
2 294 21 42(64) 2( 3)
3 98 7 14(28) 2( 3)
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015


