d03ne:: Partial Differential Equations (NAG Toolbox)

Description

nag_pde_1d_blackscholes_means (d03ne) computes the quantities

\begin{matrix} ϕ (t_{0}), & \hat{ϕ} = \frac{1}{T - t_{0}} \int_{t_{0}}^{T} ϕ (ζ) d ζ, & \bar{ϕ} = {(\frac{1}{T - t_{0}} \int_{t_{0}}^{T} ϕ^{2} (ζ) d ζ)}^{1 / 2} \end{matrix}

from a given set of values phid of a continuous time-dependent function

ϕ (t)

at a set of discrete points td, where

t_{0}

is the current time and

T

is the maturity time. Thus

\hat{ϕ}

and

\bar{ϕ}

are first and second order averages of

ϕ

over the remaining life of an option.

The function may be used in conjunction with nag_pde_1d_blackscholes_closed (d03nd) in order to value an option in the case where the risk-free interest rate

r

, the continuous dividend

q

, or the stock volatility

σ

is time-dependent and is described by values at a set of discrete times (see Use with ). This is illustrated in Example.

References

Parameters

Compulsory Input Parameters

Optional Input Parameters

Output Parameters

Error Indicators and Warnings

Accuracy

Further Comments

Timing

Use with nag_pde_1d_blackscholes_closed (d03nd)

Algorithmic Details

Example

This example demonstrates the use of the function in conjunction with nag_pde_1d_blackscholes_closed (d03nd) to solve the Black–Scholes equation for valuation of a

5

-month American call option on a non-dividend-paying stock with an exercise price of $50. The risk-free interest rate varies linearly with time and the stock volatility has a quadratic variation. Since these functions are integrated exactly by nag_pde_1d_blackscholes_means (d03ne) the solution of the Black–Scholes equation by nag_pde_1d_blackscholes_closed (d03nd) is also exact.

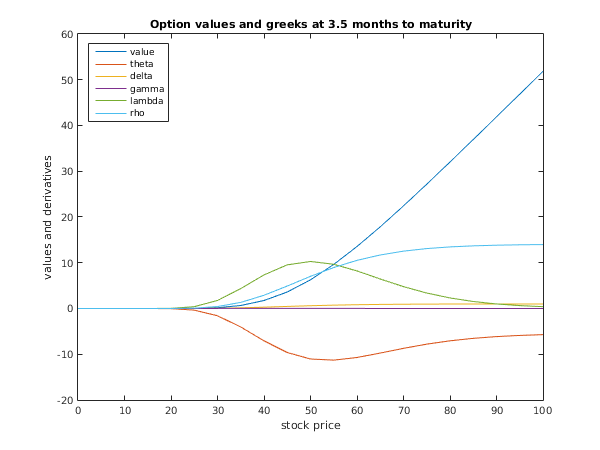
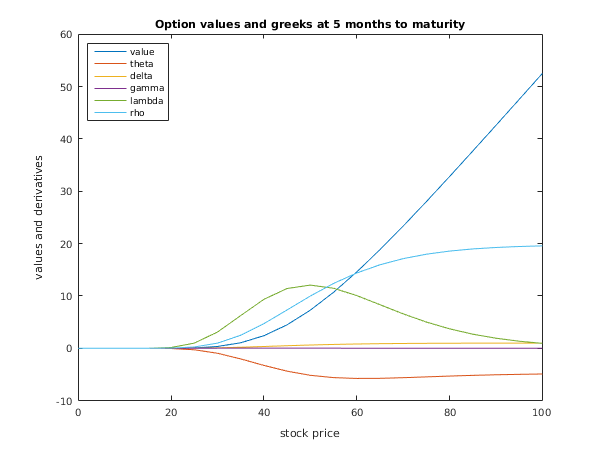
function d03ne_example


fprintf('d03ne example results\n\n');

tmat = 0.4166667;
td   = [0:0.1:0.5];
rd   = [0.1:0.01:0.15];
sigd = [0.3 0.46 0.54 0.54 0.36 0.3];

% American 5-month call option, exercise price 50

kopt = int64(2);
x = 50;
ns    = 21;  nt    = 4;
s_beg = 0;   t_beg = 0;
s_end = 100; t_end = 0.125;
tmat  = 0.4166667;
tdpar = [true; false; true];
q     = [0];

% Discretize s and t
ds = (s_end-s_beg)/(ns-1);
dt = (t_end-t_beg)/(nt-1);
s = [s_beg:ds:s_end];
t = [t_beg:dt:t_end];

f = zeros(ns,nt);
theta = f; delta = f; gamma = f; lambda = f; rho = f;

% Loop over times and prices
for j = 1:nt

  % Find average values of r and sigma
  [ra, ifail] = d03ne( ...
                          t(j), tmat, td, rd);
  [siga, ifail] = d03ne( ...
                          t(j), tmat, td, sigd);

  for i = 1:ns
    [f(i,j),theta(i,j),delta(i,j),gamma(i,j),lambda(i,j),rho(i,j),ifail] = ...
    d03nd( ...
           kopt, x, s(i), t(j), tmat, tdpar, ra, q, siga);
  end
end

% Tabulate option values only
print_greek(ns,nt,tmat,s,t,'Option Values',f);
% print_greek(ns,nt,tmat,s,t,'Theta',theta);
% print_greek(ns,nt,tmat,s,t,'Delta',delta);
% print_greek(ns,nt,tmat,s,t,'Gamma',gamma);
% print_greek(ns,nt,tmat,s,t,'Lambda',lambda);
% print_greek(ns,nt,tmat,s,t,'Rho',rho);

% plot initial and final option values and greeks 
fig1 = figure;
plot(s,f(:,1),s,theta(:,1),s,delta(:,1),s,gamma(:,1),s,lambda(:,1),s,rho(:,1));
legend('value','theta','delta','gamma','lambda','rho','Location','NorthWest');
title('Option values and greeks at 5 months to maturity');
xlabel('stock price');
ylabel('values and derivatives');
fig2 = figure;
plot(s,f(:,4),s,theta(:,4),s,delta(:,4),s,gamma(:,4),s,lambda(:,4),s,rho(:,4));
legend('value','theta','delta','gamma','lambda','rho','Location','NorthWest');
title('Option values and greeks at 3.5 months to maturity');
xlabel('stock price');
ylabel('values and derivatives');



function print_greek(ns,nt,tmat,s,t,grname,greek)

  fprintf('\n%s\n\n',grname);
  fprintf('  Stock Price  |   Time to Maturity (months)\n');
  fprintf('%16s %12.4e%12.4e%12.4e%12.4e\n', '|', 12*(tmat-t));
  fprintf('%15s+%48s\n', '---------------', ...
          '-------------------------------------------------');
  for i = 1:ns
    fprintf('%12.4e%4s %12.4e%12.4e%12.4e%12.4e\n', s(i), '|', greek(i,:));
  end

d03ne example results


Option Values

  Stock Price  |   Time to Maturity (months)
               |   5.0000e+00  4.5000e+00  4.0000e+00  3.5000e+00
---------------+-------------------------------------------------
  0.0000e+00   |   0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00
  5.0000e+00   |   8.3570e-14  1.6081e-14  1.1216e-15  1.9522e-17
  1.0000e+01   |   2.5775e-07  1.0991e-07  2.8081e-08  3.5715e-09
  1.5000e+01   |   1.7581e-04  1.0511e-04  4.6513e-05  1.3698e-05
  2.0000e+01   |   6.9193e-03  4.9696e-03  2.9591e-03  1.3701e-03
  2.5000e+01   |   7.0752e-02  5.6767e-02  4.0397e-02  2.4520e-02
  3.0000e+01   |   3.4255e-01  2.9499e-01  2.3506e-01  1.6927e-01
  3.5000e+01   |   1.0512e+00  9.4849e-01  8.1382e-01  6.5475e-01
  4.0000e+01   |   2.3997e+00  2.2341e+00  2.0134e+00  1.7424e+00
  4.5000e+01   |   4.4829e+00  4.2630e+00  3.9702e+00  3.6055e+00
  5.0000e+01   |   7.2786e+00  7.0226e+00  6.6859e+00  6.2677e+00
  5.5000e+01   |   1.0687e+01  1.0414e+01  1.0063e+01  9.6324e+00
  6.0000e+01   |   1.4580e+01  1.4305e+01  1.3959e+01  1.3546e+01
  6.5000e+01   |   1.8832e+01  1.8563e+01  1.8236e+01  1.7855e+01
  7.0000e+01   |   2.3337e+01  2.3079e+01  2.2774e+01  2.2429e+01
  7.5000e+01   |   2.8016e+01  2.7768e+01  2.7485e+01  2.7173e+01
  8.0000e+01   |   3.2809e+01  3.2573e+01  3.2308e+01  3.2022e+01
  8.5000e+01   |   3.7678e+01  3.7450e+01  3.7201e+01  3.6935e+01
  9.0000e+01   |   4.2595e+01  4.2374e+01  4.2136e+01  4.1885e+01
  9.5000e+01   |   4.7543e+01  4.7327e+01  4.7097e+01  4.6856e+01
  1.0000e+02   |   5.2510e+01  5.2298e+01  5.2074e+01  5.1840e+01

On entry,	t0 lies outside the range [ $td (1), td (ntd)$ ],
or	tmat lies outside the range [ $td (1), td (ntd)$ ],
or	$ntd < 2$ ,
or	td badly ordered,
or	$lwork < 9 \times ntd + 24$ .

NAG Toolbox: nag_pde_1d_blackscholes_means (d03ne)

▸▿ Contents

Purpose

Syntax