PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_pde_1d_blackscholes_closed (d03nd)
Purpose
nag_pde_1d_blackscholes_closed (d03nd) computes an analytic solution to the Black–Scholes equation for a certain set of option types.
Syntax
[
f,
theta,
delta,
gamma,
lambda,
rho,
ifail] = d03nd(
kopt,
x,
s,
t,
tmat,
tdpar,
r,
q,
sigma)
[
f,
theta,
delta,
gamma,
lambda,
rho,
ifail] = nag_pde_1d_blackscholes_closed(
kopt,
x,
s,
t,
tmat,
tdpar,
r,
q,
sigma)
Description
nag_pde_1d_blackscholes_closed (d03nd) computes an analytic solution to the Black–Scholes equation (see
Hull (1989) and
Wilmott et al. (1995))
for the value
of a European put or call option, or an American call option with zero dividend
. In equation
(1) is time,
is the stock price,
is the exercise price,
is the risk free interest rate,
is the continuous dividend, and
is the stock volatility. The parameter
,
and
may be either constant, or functions of time. In the latter case their average instantaneous values over the remaining life of the option should be provided to
nag_pde_1d_blackscholes_closed (d03nd). An auxiliary function
nag_pde_1d_blackscholes_means (d03ne) is available to compute such averages from values at a set of discrete times. Equation
(1) is subject to different boundary conditions depending on the type of option. For a call option the boundary condition is
where
is the maturity time of the option. For a put option the equation
(1) is subject to
nag_pde_1d_blackscholes_closed (d03nd) also returns values of the Greeks
nag_specfun_opt_bsm_greeks (s30ab) also computes the European option price given by the Black–Scholes–Merton formula together with a more comprehensive set of sensitivities (Greeks).
Further details of the analytic solution returned are given in
Algorithmic Details.
References
Hull J (1989) Options, Futures and Other Derivative Securities Prentice–Hall
Wilmott P, Howison S and Dewynne J (1995) The Mathematics of Financial Derivatives Cambridge University Press
Parameters
Compulsory Input Parameters
- 1:
– int64int32nag_int scalar
-
Specifies the kind of option to be valued:
- A European call option.
- An American call option.
- A European put option.
Constraints:
- , or ;
- if , .
- 2:
– double scalar
-
The exercise price .
Constraint:
.
- 3:
– double scalar
-
The stock price at which the option value and the Greeks should be evaluated.
Constraint:
.
- 4:
– double scalar
-
The time at which the option value and the Greeks should be evaluated.
Constraint:
.
- 5:
– double scalar
-
The maturity time of the option.
Constraint:
.
- 6:
– logical array
-
Specifies whether or not various arguments are time-dependent. More precisely, is time-dependent if and constant otherwise. Similarly, specifies whether is time-dependent and specifies whether is time-dependent.
- 7:
– double array
-
The dimension of the array
r
must be at least
if
, and at least
otherwise
If
then
must contain the constant value of
. The remaining elements need not be set.
If
then
must contain the value of
at time
t and
must contain its average instantaneous value over the remaining life of the option:
The auxiliary function
nag_pde_1d_blackscholes_means (d03ne) may be used to construct
r from a set of values of
at discrete times.
- 8:
– double array
-
The dimension of the array
q
must be at least
if
, and at least
otherwise
If
then
must contain the constant value of
. The remaining elements need not be set.
If
then
must contain the constant value of
and
must contain its average instantaneous value over the remaining life of the option:
The auxiliary function
nag_pde_1d_blackscholes_means (d03ne) may be used to construct
q from a set of values of
at discrete times.
- 9:
– double array
-
The dimension of the array
sigma
must be at least
if
, and at least
otherwise
If
then
must contain the constant value of
. The remaining elements need not be set.
If
then
must contain the value of
at time
t,
the average instantaneous value
, and
the second-order average
, where:
The auxiliary function
nag_pde_1d_blackscholes_means (d03ne) may be used to compute
sigma from a set of values at discrete times.
Constraints:
- if , ;
- if , , for .
Optional Input Parameters
None.
Output Parameters
- 1:
– double scalar
-
The value
of the option at the stock price
s and time
t.
- 2:
– double scalar
- 3:
– double scalar
- 4:
– double scalar
- 5:
– double scalar
- 6:
– double scalar
-
The values of various Greeks at the stock price
s and time
t, as follows:
- 7:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
| On entry, | , |
| or | , |
| or | when , |
| or | , |
| or | , |
| or | , |
| or | , |
| or | , with , |
| or | , with , for some , or . |
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
Given accurate values of
r,
q and
sigma no further approximations are made in the evaluation of the Black–Scholes analytic formulae, and the results should therefore be within machine accuracy. The values of
r,
q and
sigma returned from
nag_pde_1d_blackscholes_means (d03ne) are exact for polynomials of degree up to
.
Further Comments
Algorithmic Details
The Black–Scholes analytic formulae are used to compute the solution. For a European call option these are as follows:
where
is the cumulative Normal distribution function and
is its derivative
The functions
,
,
and
are average values of
,
and
over the time to maturity:
The Greeks are then calculated as follows:
Note: that is obtained from substitution of other Greeks in the Black–Scholes partial differential equation, rather than differentiation of . The values of , and appearing in its definition are the instantaneous values, not the averages. Note also that both the first-order average and the second-order average appear in the expression for . This results from the fact that is the derivative of with respect to , not .
For a European put option the equivalent equations are:
The analytic solution for an American call option with is identical to that for a European call, since early exercise is never optimal in this case. For all other cases no analytic solution is known.
Example
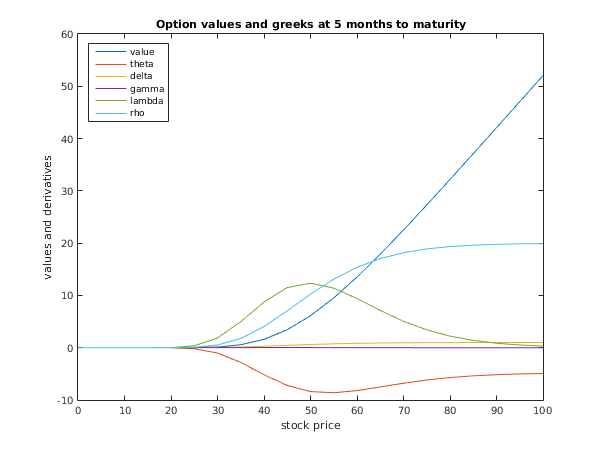
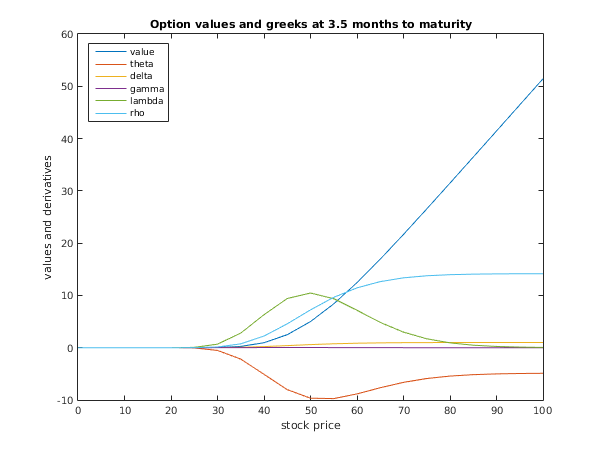
This example solves the Black–Scholes equation for valuation of a -month American call option on a non-dividend-paying stock with an exercise price of $50. The risk-free interest rate is 10% per annum, and the stock volatility is 40% per annum.
The option is valued at a range of times and stock prices.
Open in the MATLAB editor:
d03nd_example
function d03nd_example
fprintf('d03nd example results\n\n');
kopt = int64(2);
x = 50;
ns = 21; nt = 4;
s_beg = 0; t_beg = 0;
s_end = 100; t_end = 0.125;
tmat = 0.4166667;
tdpar = [false; false; false];
r = [0.1];
q = [0];
sigma = [0.4];
ds = (s_end-s_beg)/(ns-1);
dt = (t_end-t_beg)/(nt-1);
s = [s_beg:ds:s_end];
t = [t_beg:dt:t_end];
f = zeros(ns,nt);
theta = f; delta = f; gamma = f; lambda = f; rho = f;
for j = 1:nt
for i = 1:ns
[f(i,j),theta(i,j),delta(i,j),gamma(i,j),lambda(i,j),rho(i,j),ifail] = ...
d03nd( ...
kopt, x, s(i), t(j), tmat, tdpar, r, q, sigma);
end
end
print_greek(ns,nt,tmat,s,t,'Option Values',f);
fig1 = figure;
plot(s,f(:,1),s,theta(:,1),s,delta(:,1),s,gamma(:,1),s,lambda(:,1),s,rho(:,1));
legend('value','theta','delta','gamma','lambda','rho','Location','NorthWest');
title('Option values and greeks at 5 months to maturity');
xlabel('stock price');
ylabel('values and derivatives');
fig2 = figure;
plot(s,f(:,4),s,theta(:,4),s,delta(:,4),s,gamma(:,4),s,lambda(:,4),s,rho(:,4));
legend('value','theta','delta','gamma','lambda','rho','Location','NorthWest');
title('Option values and greeks at 3.5 months to maturity');
xlabel('stock price');
ylabel('values and derivatives');
function print_greek(ns,nt,tmat,s,t,grname,greek)
fprintf('\n%s\n\n',grname);
fprintf(' Stock Price | Time to Maturity (months)\n');
fprintf('%16s %12.4e%12.4e%12.4e%12.4e\n', '|', 12*(tmat-t));
fprintf('%15s+%48s\n', '---------------', ...
'-------------------------------------------------');
for i = 1:ns
fprintf('%12.4e%4s %12.4e%12.4e%12.4e%12.4e\n', s(i), '|', greek(i,:));
end
d03nd example results
Option Values
Stock Price | Time to Maturity (months)
| 5.0000e+00 4.5000e+00 4.0000e+00 3.5000e+00
---------------+-------------------------------------------------
0.0000e+00 | 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00
5.0000e+00 | 4.4491e-19 4.5989e-21 1.5461e-23 1.0478e-26
1.0000e+01 | 5.5566e-10 5.5129e-11 3.1298e-12 8.0281e-14
1.5000e+01 | 4.7337e-06 1.2187e-06 2.2774e-07 2.7003e-08
2.0000e+01 | 7.2236e-04 3.1054e-04 1.1005e-04 2.9678e-05
2.5000e+01 | 1.6557e-02 9.6610e-03 5.0099e-03 2.2012e-03
3.0000e+01 | 1.3307e-01 9.4037e-02 6.1869e-02 3.6848e-02
3.5000e+01 | 5.6631e-01 4.5257e-01 3.4667e-01 2.5053e-01
4.0000e+01 | 1.6004e+00 1.3850e+00 1.1699e+00 9.5640e-01
4.5000e+01 | 3.4384e+00 3.1328e+00 2.8168e+00 2.4891e+00
5.0000e+01 | 6.1165e+00 5.7600e+00 5.3874e+00 4.9960e+00
5.5000e+01 | 9.5300e+00 9.1645e+00 8.7846e+00 8.3882e+00
6.0000e+01 | 1.3509e+01 1.3163e+01 1.2808e+01 1.2445e+01
6.5000e+01 | 1.7883e+01 1.7568e+01 1.7251e+01 1.6932e+01
7.0000e+01 | 2.2513e+01 2.2230e+01 2.1949e+01 2.1671e+01
7.5000e+01 | 2.7301e+01 2.7045e+01 2.6792e+01 2.6544e+01
8.0000e+01 | 3.2182e+01 3.1946e+01 3.1713e+01 3.1485e+01
8.5000e+01 | 3.7117e+01 3.6894e+01 3.6674e+01 3.6458e+01
9.0000e+01 | 4.2081e+01 4.1868e+01 4.1656e+01 4.1446e+01
9.5000e+01 | 4.7062e+01 4.6854e+01 4.6647e+01 4.6441e+01
1.0000e+02 | 5.2052e+01 5.1847e+01 5.1643e+01 5.1439e+01
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015

