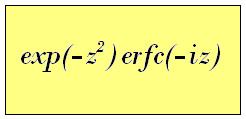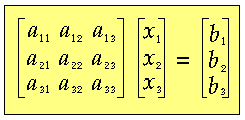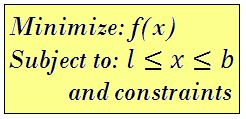Calling NAG Library Routines from Octave

NAG Technical Report TR 4/09

Anna Kwiczala
Numerical Algorithms Group, May 2009

Abstract

This report gives detailed instructions on how to call routines in the NAG C and Fortran Libraries from the Octave programming environment.

Contents

  1. Introduction
  2. C++ code and Oct-Files
  3. Examples
  4. Summary
  5. References

1. Introduction

Octave [1] is a freely redistributable programming language for numerical computations. It is mostly compatible with MATLAB. The NAG Libraries [2] contain a large selection of numerical and statistical routines, which can be accessed from different languages [3]. This article gives a brief introduction to one of the methods and examples of calling NAG routines from within Octave.

Octave can be extended by dynamically linked functions [4], which are used in the same way as Octave functions. Octave has been written in C++, so it is not surprising that the easiest way of extending it is by writing the linking code in that language. It can be called by Octave directly through its native oct-file interface. Due to the fact that C functions can easily be called from C++, our best choice is to use C++ code together with the NAG C Library.

2. C++ code and Oct-Files

Octave comes with a ready-made script mkoctfile, which can be used to compile C++ code into oct-files. All we have to do is to write a C++ function calling one of the NAG routines and then use the script. To define the entry point into the dynamically linked function, we need to use the Octave DEFUN_DLD macro in our C++ code. Therefore, our function will look like this:

  #include <octave/oct.h>
  #include <appropriate NAG header files>

     DEFUN_DLD (function_name, args, nargout,
       "Function description")
     {
       octave_value_list retval;

  // retrieve input arguments from args
  // call NAG routine
  // assign output arguments to retval

       return retval;
     }

where:

  • oct.h contains most of the necessary definitions for an oct-file in Octave;
  • function_name will be our function's name seen in Octave and it must match the file's name, but be different from any NAG routine names;
  • args is the list of arguments to the function of type octave_value_list;
  • nargout is the number of output arguments;
  • "Function description" is the string that will be seen as the function help text;
  • the return type is always octave_value_list.

3. Examples

The rest of the code required will be easier to demonstrate with the use of examples. The code for this article was tested on a Linux machine running 64-bit Fedora 8 (Werewolf) with Octave 3.0.3, plus c++ (GCC) 4.3.3, gcc (GCC) 4.3.3, GNU Fortran (GCC) 4.3.3, Mark 8 of the NAG C Library and Mark 22 of the NAG FORTRAN Library.

3.1 Example 1  Log gamma function ln Γ(x)

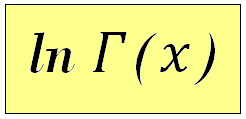lgamma The simplest example: we call a function with only one return value - the ln Γ'(x) logarithm gamma function routine nag_log_gamma (s14abc) from the NAG C Library.

3.2 Example 2  Scaled complex complement of error function, exp(-z2)erfc(-iz)

erfc We call a function with complex input and output values - nag_complex_erfc (s15ddc), which computes values of the function w(z)=exp(-z2)erfc(-iz), for complex z. Complex numbers are stored differently in Octave and NAG C Library, so extra code is required to copy input data from Octave complex type to NAG complex type and the result back from NAG complex type to Octave complex type.

3.3 Example 3  Approximate solution of complex simultaneous linear equations AX = B

lineq We call a function which takes and returns complex arrays - nag_complex_lu_solve_mult_rhs (f04akc). The function calculates the approximate solution of a set of complex linear equations with multiple right-hand sides AX=B, where A has been factorized by nag_complex_lu (f03ahc). Again, some copying between Octave and NAG complex types is required.

3.4 Example 4  Solving a nonlinear minimization problem

minimization In this example we call the nonlinear minimization routine nag_opt_nlp (e04ucc). The routine takes as input two user-supplied functions. We show two ways of supplying the functions - either as C code or Octave code. We also demonstrate how to pass Octave arrays and matrices into C.

3.5 Example 5  Univariate time series, seasonal and non-seasonal differencing

tsa We call a function from NAG Fortran Library - G13AAF. The function carries out non-seasonal and seasonal differencing on a time series. It returns the differenced values and data which allow the original series to be reconstituted from the differenced series. We use NAG header files [5] for the NAG Fortran Library.

5. Summary

Octave contains many tools that make extending it fairly easy. The method used in this article is just one of a few possible approaches which we believe is the easiest one. If you want to try different methods, consult Dynamically Linked Functions section on Octave website [4].

References

Copyright 2009 Numerical Algorithms Group