s15af: FL CL CPP AD

NAG CL Interface
s15afc (dawson)

Keyword Search:

NAG Library Manual, Mark 28.3

Interfaces: FL CL CPP AD

NAG CL Interface Introduction

S (Specfun) Chapter Contents

S (Specfun) Chapter Introduction

s15af: FL CL CPP AD

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

▸▿ 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

Settings help

CL Name Style:
Short (a00aac)
Long (impl_details)
Full (nag_info_impl_details)

1 Purpose

s15afc returns a value for Dawson's Integral,

F (x)

2 Specification

#include <nag.h>

double

s15afc (double x)

The function may be called by the names: s15afc, nag_specfun_dawson or nag_dawson.

3 Description

s15afc evaluates an approximation for Dawson's Integral

F (x) = e^{- x^{2}} \int_{0}^{x} e^{t^{2}} d t .

The function is based on two Chebyshev expansions:

For

0 < | x | \leq 4

F (x) = x \sum_{r = 0}^{'} a_{r} T_{r} (t),   where t = 2 {(\frac{x}{4})}^{2} - 1 .

For

| x | > 4

F (x) = \frac{1}{x} \sum_{r = 0}^{'} b_{r} T_{r} (t),   where t = 2 {(\frac{4}{x})}^{2} - 1 .

For

| x |

near zero,

F (x) ≃ x

, and for

| x |

large,

F (x) ≃ \frac{1}{2 x}

. These approximations are used for those values of

x

for which the result is correct to machine precision.

4 References

NIST Digital Library of Mathematical Functions

5 Arguments

1: $x$ – double Input: On entry: the argument $x$ of the function.

6 Error Indicators and Warnings

None.

7 Accuracy

Let

δ

and

ε

be the relative errors in the argument and result respectively.

δ

is considerably greater than the machine precision (i.e., if

δ

is due to data errors etc.), then

ε

and

δ

are approximately related by:

ε ≃ | \frac{x (1 - 2 x F (x))}{F (x)} | δ .

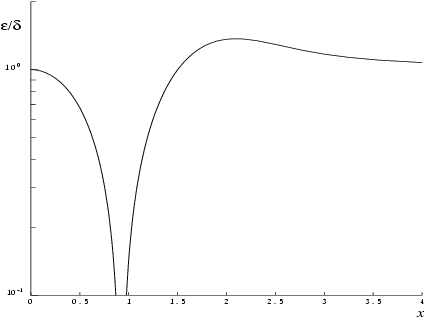
The following graph shows the behaviour of the error amplification factor

| \frac{x (1 - 2 x F (x))}{F (x)} |

Figure 1

However, if

δ

is of the same order as machine precision, then rounding errors could make

ε

somewhat larger than the above relation indicates. In fact

ε

will be largely independent of

x

δ

, but will be of the order of a few times the machine precision.

8 Parallelism and Performance

s15afc is not threaded in any implementation.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

s15af: FL CL CPP AD

NAG CL Interfaces15afc (dawson)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

NAG CL Interface
s15afc (dawson)