1: $x$ – Real (Kind=nag_wp) Input: On entry: the argument $x$ of the function.

Constraint: $x > 0.0$ .
2: $ifail$ – Integer Input/Output: On entry: ifail must be set to $0$ , $- 1$ or $1$ to set behaviour on detection of an error; these values have no effect when no error is detected.
A value of $0$ causes the printing of an error message and program execution will be halted; otherwise program execution continues. A value of $- 1$ means that an error message is printed while a value of $1$ means that it is not.

If halting is not appropriate, the value $- 1$ or $1$ is recommended. If message printing is undesirable, then the value $1$ is recommended. Otherwise, the value $0$ is recommended. When the value $- 1$ or $1$ is used it is essential to test the value of ifail on exit.

On exit: $ifail = 0$ unless the routine detects an error or a warning has been flagged (see Section 6).

6 Error Indicators and Warnings

If on entry

ifail = 0

- 1

, explanatory error messages are output on the current error message unit (as defined by x04aaf).

Errors or warnings detected by the routine:

$ifail = 1$: On entry, $x = 〈value〉$ .
Constraint: $x > 0.0$ .
The routine has been called with an argument less than or equal to zero for which $Ci (x)$ is not defined.

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.
See Section 7 in the Introduction to the NAG Library FL Interface for further information.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.
See Section 8 in the Introduction to the NAG Library FL Interface for further information.

$ifail = - 999$: Dynamic memory allocation failed.
See Section 9 in the Introduction to the NAG Library FL Interface for further information.

7 Accuracy

E

and

ε

are the absolute and relative errors in the result and

δ

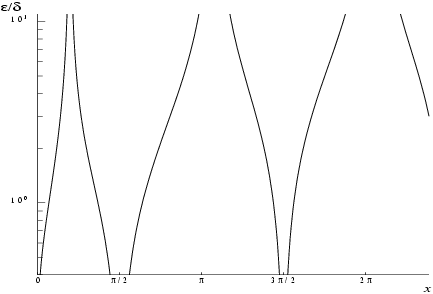
is the relative error in the argument then in principle these are related by

|E| ≃ |δ \cos x| and ​ |ε| ≃ |\frac{δ \cos x}{Ci (x)}| .

That is accuracy will be limited by machine precision near the origin and near the zeros of

\cos x

, but near the zeros of

Ci (x)

only absolute accuracy can be maintained.

The behaviour of this amplification is shown in Figure 1.

Figure 1

For large values of

x

Ci (x) \sim \frac{\sin x}{x}

therefore

ε \sim δ x \cot x

and since

δ

is limited by the finite precision of the machine it becomes impossible to return results which have any relative accuracy. That is, when

x \geq 1 / δ

we have that

|Ci (x)| \leq 1 / x \sim E

and hence is not significantly different from zero.

Hence

x_{hi}

is chosen such that for values of

x \geq x_{hi}

Ci (x)

in principle would have values less than the machine precision and so is essentially zero.

8 Parallelism and Performance

s13acf is not threaded in any implementation.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

s13ac: FL CL CPP AD

NAG FL Interfaces13acf (integral_​cos)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

NAG FL Interface
s13acf (integral_cos)