g03ehc produces a dendrogram from the results of
g03ecc.
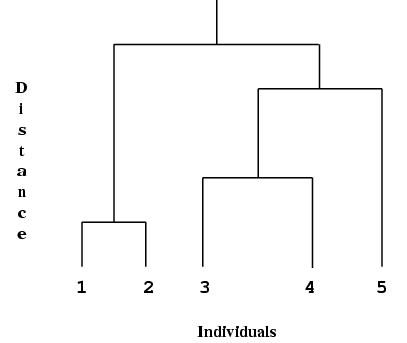
Hierarchical cluster analysis, as performed by
g03ecc can be represented by a tree that shows at which distance the clusters merge. Such a tree is known as a dendrogram. See
Everitt (1974) and
Krzanowski (1990) for examples of dendrograms. A simple example is,
The end-points of the dendrogram represent the objects that have been clustered. They should be in a suitable order as given by
g03ecc. Object 1 is always the first object. In the example above the height represents the distance at which the clusters merge.
The dendrogram is produced in an array of character pointers using the ordering and distances provided by
g03ecc. Suitable characters are used to represent parts of the tree.
There are four possible orientations for the dendrogram. The example above has the end-points at the bottom of the diagram which will be referred to as south. If the dendrogram was the other way around with the end-points at the top of the diagram then the orientation would be north. If the end-points are at the left-hand or right-hand side of the diagram the orientation is west or east. Different symbols are used for east/west and north/south orientations.
Not applicable.
The scale of the dendrogram is controlled by
dstep. The smaller the value of
dstep the greater the amount of detail that will be given. However,
nsym will have to be larger to give the full dendrogram. The range of distances represented by the dendrogram is
dmin to
. The values of
dmin,
dstep and
nsym can thus be set so that only part of the dendrogram is produced.
The dendrogram does not include any labelling of the objects. You can print suitable labels using the ordering given by the array
iord returned by
g03ecc.
Data consisting of three variables on five objects are read in. Euclidean squared distances are computed using
g03eac and median clustering performed by
g03ecc.
g03ehc is used to produce a dendrogram with orientation east and a dendrogram with orientation south. The two dendrograms are printed.
Note the use of
g03xzc to free the memory allocated internally to the character array pointed to by
c.