NAG FL Interface
s15aff (dawson)

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

1: $\mathbf{x}$ – Real (Kind=nag_wp) Input

On entry: the argument $x$ of the function.

2: $\mathbf{ifail}$ – Integer Input/Output

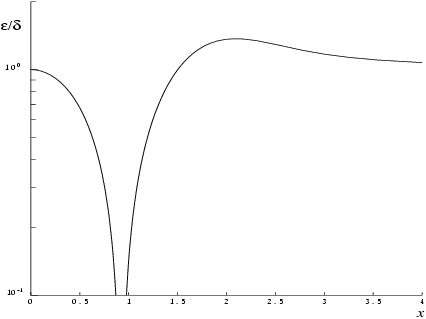
On entry: ifail must be set to $0$, $-1\text{ or }1$. If you are unfamiliar with this argument you should refer to Section 4 in the Introduction to the NAG Library FL Interface for details.

For environments where it might be inappropriate to halt program execution when an error is detected, the value $-1\text{ or }1$ is recommended. If the output of error messages is undesirable, then the value $1$ is recommended. Otherwise, if you are not familiar with this argument, the recommended value is $0$. When the value $-\mathbf{1}\text{ or }\mathbf{1}$ is used it is essential to test the value of ifail on exit.

On exit: $\mathbf{ifail}=\mathbf{0}$ unless the routine detects an error or a warning has been flagged (see Section 6).

6 Error Indicators and Warnings

7 Accuracy

If $\delta$ is considerably greater than the machine precision (i.e., if $\delta$ is due to data errors etc.), then $\epsilon$ and $\delta$ are approximately related by:

$$\epsilon \simeq \left|\frac{x\left(1-2xF\left(x\right)\right)}{F\left(x\right)}\right|\delta \text{.}$$

The following graph shows the behaviour of the error amplification factor $\left|\frac{x\left(1-2xF\left(x\right)\right)}{F\left(x\right)}\right|$:

Figure 1

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results