Integer, Intent (In)	::	n
Integer, Intent (Inout)	::	ifail
Integer, Intent (Out)	::	ivalid(n)
Real (Kind=nag_wp), Intent (In)	::	x(n)
Real (Kind=nag_wp), Intent (Out)	::	f(n)

C Header Interface

#include <nag.h>

void	s14anf_ (const Integer n, const double x[], double f[], Integer ivalid[], Integer ifail)

The routine may be called by the names s14anf or nagf_specfun_gamma_vector.

3 Description

s14anf evaluates an approximation to the gamma function

Γ (x)

for an array of arguments

x_{i}

, for

i = 1, 2, \dots, n

. The routine is based on the Chebyshev expansion:

Γ (1 + u) = \sum_{r = 0}^{'} a_{r} T_{r} (t)

where

0 \leq u < 1, t = 2 u - 1,

and uses the property

Γ (1 + x) = x Γ (x)

. If

x = N + 1 + u

where

N

is integral and

0 \leq u < 1

then it follows that:

for $N > 0$ ,	$Γ (x) = (x - 1) (x - 2) \dots (x - N) Γ (1 + u)$ ,
for $N = 0$ ,	$Γ (x) = Γ (1 + u)$ ,
for $N < 0$ ,	$Γ (x) = \frac{Γ (1 + u)}{x (x + 1) (x + 2) \dots (x - N - 1)}$ .

There are four possible failures for this routine:

(i)if $x$ is too large, there is a danger of overflow since $Γ (x)$ could become too large to be represented in the machine;
(ii)if $x$ is too large and negative, there is a danger of underflow;
(iii)if $x$ is equal to a negative integer, $Γ (x)$ would overflow since it has poles at such points;
(iv)if $x$ is too near zero, there is again the danger of overflow on some machines. For small $x$ , $Γ (x) ≃ 1 / x$ , and on some machines there exists a range of nonzero but small values of $x$ for which $1 / x$ is larger than the greatest representable value.

4 References

NIST Digital Library of Mathematical Functions

5 Arguments

1: $n$ – Integer Input

On entry:

n

, the number of points.

Constraint:

n \geq 0

2: $x (n)$ – Real (Kind=nag_wp) array Input

On entry: the argument

x_{i}

of the function, for

i = 1, 2, \dots, n

Constraint:

x (i) \notin ℤ_{0}^{-}

, for

i = 1, 2, \dots, n

3: $f (n)$ – Real (Kind=nag_wp) array Output

On exit:

Γ (x_{i})

, the function values.

4: $ivalid (n)$ – Integer array Output

On exit:

ivalid (i)

contains the error code for

x_{i}

, for

i = 1, 2, \dots, n

$ivalid (i) = 0$: No error.
$ivalid (i) = 1$: $x_{i}$ is too large and positive. $f (i)$ contains the approximate value of $Γ (x_{i})$ at the nearest valid argument. The threshold value is the same as for $ifail = 1$ in s14aaf, as defined in the Users' Note for your implementation.
$ivalid (i) = 2$: $x_{i}$ is too large and negative. $f (i)$ contains zero. The threshold value is the same as for $ifail = 2$ in s14aaf, as defined in the Users' Note for your implementation.
$ivalid (i) = 3$: $x_{i}$ is too close to zero. $f (i)$ contains the approximate value of $Γ (x_{i})$ at the nearest valid argument. The threshold value is the same as for $ifail = 2$ in s14aaf, as defined in the Users' Note for your implementation.
$ivalid (i) = 4$: $x_{i}$ is a negative integer, at which values $Γ (x_{i})$ are infinite. $f (i)$ contains a large positive value.

5: $ifail$ – Integer Input/Output

On entry: ifail must be set to

0

- 1 or 1

. If you are unfamiliar with this argument you should refer to Section 4 in the Introduction to the NAG Library FL Interface for details.

For environments where it might be inappropriate to halt program execution when an error is detected, the value

- 1 or 1

is recommended. If the output of error messages is undesirable, then the value

1

is recommended. Otherwise, if you are not familiar with this argument, the recommended value is

0

. When the value $- 1 or 1$ is used it is essential to test the value of ifail on exit.

On exit:

ifail = 0

unless the routine detects an error or a warning has been flagged (see Section 6).

6 Error Indicators and Warnings

If on entry

ifail = 0

- 1

, explanatory error messages are output on the current error message unit (as defined by x04aaf).

Errors or warnings detected by the routine:

$ifail = 1$: On entry, at least one value of x was invalid.
Check ivalid for more information.

$ifail = 2$: On entry, $n = 〈value〉$ .
Constraint: $n \geq 0$ .

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.
See Section 7 in the Introduction to the NAG Library FL Interface for further information.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.
See Section 8 in the Introduction to the NAG Library FL Interface for further information.

$ifail = - 999$: Dynamic memory allocation failed.
See Section 9 in the Introduction to the NAG Library FL Interface for further information.

7 Accuracy

Let

δ

and

ε

be the relative errors in the argument and the result respectively. If

δ

is somewhat larger than the machine precision (i.e., is due to data errors etc.), then

ε

and

δ

are approximately related by:

ε ≃ |x Ψ (x)| δ

(provided

ε

is also greater than the representation error). Here

Ψ (x)

is the digamma function

\frac{Γ^{'} (x)}{Γ (x)}

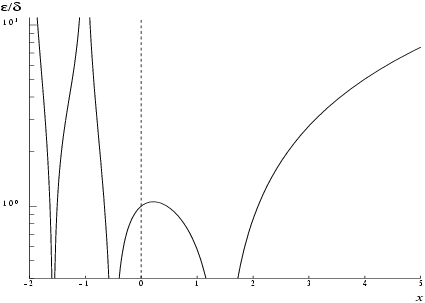
. Figure 1 shows the behaviour of the error amplification factor

|x Ψ (x)|

δ

is of the same order as machine precision, then rounding errors could make

ε

slightly larger than the above relation predicts.

There is clearly a severe, but unavoidable, loss of accuracy for arguments close to the poles of

Γ (x)

at negative integers. However, relative accuracy is preserved near the pole at

x = 0

right up to the point of failure arising from the danger of overflow.

Also, accuracy will necessarily be lost as

x

becomes large since in this region

ε ≃ δ x \ln x .

However, since

Γ (x)

increases rapidly with

x

, the routine must fail due to the danger of overflow before this loss of accuracy is too great. (For example, for

x = 20

, the amplification factor

≃ 60

Figure 1

8 Parallelism and Performance

s14anf is not threaded in any implementation.

9 Further Comments

None.

10 Example

This example reads values of x from a file, evaluates the function at each value of

x_{i}

and prints the results.

Interfaces: FL CL AD

NAG FL Interface Introduction

S (Specfun) Chapter Contents

S (Specfun) Chapter Introduction

s14an: FL CL AD

NAG FL Interfaces14anf (gamma_​vector)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

NAG FL Interface
s14anf (gamma_vector)