1: $x$ – Real (Kind=nag_wp) Input: On entry: the argument $x$ of the function.

Constraint: $|x| < 1.0$ .
2: $ifail$ – Integer Input/Output: On entry: ifail must be set to $0$ , $- 1 or 1$ . If you are unfamiliar with this argument you should refer to Section 4 in the Introduction to the NAG Library FL Interface for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value $- 1 or 1$ is recommended. If the output of error messages is undesirable, then the value $1$ is recommended. Otherwise, if you are not familiar with this argument, the recommended value is $0$ . When the value $- 1 or 1$ is used it is essential to test the value of ifail on exit.

On exit: $ifail = 0$ unless the routine detects an error or a warning has been flagged (see Section 6).

6 Error Indicators and Warnings

If on entry

ifail = 0

- 1

, explanatory error messages are output on the current error message unit (as defined by x04aaf).

Errors or warnings detected by the routine:

$ifail = 1$: On entry, $x = 〈value〉$ .
Constraint: $|x| < 1$ .
The routine has been called with an argument greater than or equal to $1.0$ in magnitude, for which $arctanh$ is not defined.

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.
See Section 7 in the Introduction to the NAG Library FL Interface for further information.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.
See Section 8 in the Introduction to the NAG Library FL Interface for further information.

$ifail = - 999$: Dynamic memory allocation failed.
See Section 9 in the Introduction to the NAG Library FL Interface for further information.

7 Accuracy

δ

and

ε

are the relative errors in the argument and result, respectively, then in principle

|ε| ≃ |\frac{x}{(1 - x^{2}) arctanh x} \times δ| .

That is, the relative error in the argument,

x

, is amplified by at least a factor

\frac{x}{(1 - x^{2}) arctanh x}

in the result. The equality should hold if

δ

is greater than the machine precision (

δ

due to data errors etc.) but if

δ

is simply due to round-off in the machine representation then it is possible that an extra figure may be lost in internal calculation round-off.

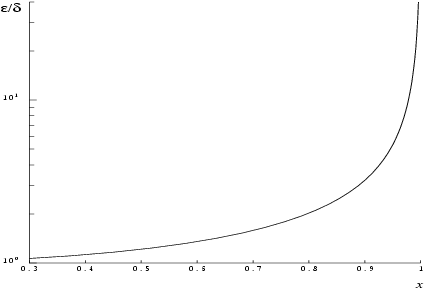
The behaviour of the amplification factor is shown in the following graph:

Figure 1

The factor is not significantly greater than one except for arguments close to

|x| = 1

. However, in the region where

|x|

is close to one,

1 - |x| \sim δ

, the above analysis is inapplicable since

x

is bounded by definition,

|x| < 1

. In this region where arctanh is tending to infinity we have

ε \sim 1 / \ln δ

which implies an obvious, unavoidable serious loss of accuracy near

|x| \sim 1

, e.g., if

x

and

1

agree to

6

significant figures, the result for

arctanh x

would be correct to at most about one figure.

8 Parallelism and Performance

s11aaf is not threaded in any implementation.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

Interfaces: FL CL AD

NAG FL Interface Introduction

S (Specfun) Chapter Contents

S (Specfun) Chapter Introduction

s11aa: FL CL AD

NAG FL Interfaces11aaf (arctanh)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

NAG FL Interface
s11aaf (arctanh)