Integer, External	::	isin
Integer, Intent (In)	::	m, n, nb, sdindx, sddist
Integer, Intent (Inout)	::	ifail
Integer, Intent (Out)	::	npts, indx(4,sdindx)
Real (Kind=nag_wp), Intent (In)	::	h
Real (Kind=nag_wp), Intent (Out)	::	places(2,sdindx), dist(4,sddist)

C Header Interface

#include <nag.h>

void	d03maf_ (const double h, const Integer m, const Integer n, const Integer nb, Integer npts, double places[], Integer indx[], const Integer sdindx, Integer (NAG_CALL isin)(const double x, const double y), double dist[], const Integer sddist, Integer *ifail)

The routine may be called by the names d03maf or nagf_pde_dim2_triangulate.

3 Description

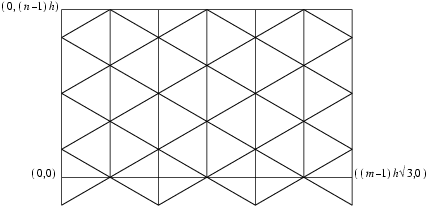
d03maf begins with a uniform triangular grid as shown in Figure 1 and assumes that the region to be triangulated lies within the rectangle given by the inequalities

0 < x < \sqrt{3} (m - 1) h, 0 < y < (n - 1) h .

This rectangle is drawn in bold in Figure 1. The region is specified by the isin which must determine whether any given point

(x, y)

lies in the region. The uniform grid is processed column-wise, with

(x_{1}, y_{1})

preceding

(x_{2}, y_{2})

x_{1} < x_{2}

x_{1} = x_{2}

y_{1} < y_{2}

. Points near the boundary are moved onto it and points well outside the boundary are omitted. The direction of movement is chosen to avoid pathologically thin triangles. The points accepted are numbered in exactly the same order as the corresponding points of the uniform grid were scanned. The output consists of the

x, y

coordinates of all grid points and integers indicating whether they are internal and to which other points they are joined by triangle sides.

The mesh size

h

must be chosen small enough for the essential features of the region to be apparent from testing all points of the original uniform grid for being inside the region. For instance if any hole is within

2 h

of another hole or the outer boundary then a triangle may be found with all vertices within

\frac{1}{2} h

of a boundary. Such a triangle is taken to be external to the region so the effect will be to join the hole to another hole or to the external region.

Further details of the algorithm are given in the references.

Figure 1

4 References

Reid J K (1970) Fortran subroutines for the solutions of Laplace's equation over a general routine in two dimensions Harwell Report TP422

Reid J K (1972) On the construction and convergence of a finite-element solution of Laplace's equation J. Instr. Math. Appl. 9 1–13

5 Arguments

1: $h$ – Real (Kind=nag_wp) Input

On entry:

h

, the required length for the sides of the triangles of the uniform mesh.

2: $m$ – Integer Input

3: $n$ – Integer Input

On entry: values

m

and

n

such that all points

(x, y)

inside the region satisfy the inequalities

\begin{array}{l} 0 \leq x \leq \sqrt{3} (m - 1) h, \\ 0 \leq y \leq (n - 1) h . \end{array}

Constraint:

m = n > 2

4: $nb$ – Integer Input

On entry: the number of times a triangle side is bisected to find a point on the boundary. A value of

10

is adequate for most purposes (see Section 7).

Constraint:

nb \geq 1

5: $npts$ – Integer Output

On exit: the number of points in the triangulation.

6: $places (2, sdindx)$ – Real (Kind=nag_wp) array Output

On exit: the

x

and

y

coordinates respectively of the

i

th point of the triangulation.

7: $indx (4, sdindx)$ – Integer array Output

On exit:

indx (1, i)

contains

i

if point

i

is inside the region and

- i

if it is on the boundary. For each triangle side between points

i

and

j

with

j > i

indx (k, i)

k > 1

, contains

j

- j

according to whether point

j

is internal or on the boundary. There can never be more than three such points. If there are less, some values

indx (k, i)

k > 1

, are zero.

8: $sdindx$ – Integer Input

On entry: the second dimension of the arrays places and indx as declared in the (sub)program from which d03maf is called.

Constraint:

sdindx \geq npts

9: $isin$ – Integer Function, supplied by the user. External Procedure

isin must return the value

1

if the given point

(x, y)

lies inside the region, and

0

if it lies outside.

The specification of isin is:

Fortran Interface

Function isin (

x, y)

Integer	::	isin
Real (Kind=nag_wp), Intent (In)	::	x, y

C Header Interface

Integer

isin_ (const double *x, const double *y)

1: $x$ – Real (Kind=nag_wp) Input
2: $y$ – Real (Kind=nag_wp) Input: On entry: the coordinates of the given point.

isin must either be a module subprogram USEd by, or declared as EXTERNAL in, the (sub)program from which d03maf is called. Arguments denoted as Input must not be changed by this procedure.

10: $dist (4, sddist)$ – Real (Kind=nag_wp) array Workspace

11: $sddist$ – Integer Input

On entry: the second dimension of the array dist as declared in the (sub)program from which d03maf is called.

Constraint:

sddist \geq 4 n

12: $ifail$ – Integer Input/Output

On entry: ifail must be set to

0

- 1 or 1

. If you are unfamiliar with this argument you should refer to Section 4 in the Introduction to the NAG Library FL Interface for details.

For environments where it might be inappropriate to halt program execution when an error is detected, the value

- 1 or 1

is recommended. If the output of error messages is undesirable, then the value

1

is recommended. Otherwise, if you are not familiar with this argument, the recommended value is

0

. When the value $- 1 or 1$ is used it is essential to test the value of ifail on exit.

On exit:

ifail = 0

unless the routine detects an error or a warning has been flagged (see Section 6).

6 Error Indicators and Warnings

If on entry

ifail = 0

- 1

, explanatory error messages are output on the current error message unit (as defined by x04aaf).

Errors or warnings detected by the routine:

$ifail = 1$: sdindx is too small: $sdindx = 〈value〉$ .

$ifail = 2$: A point inside the region violates one of the constraints.

$ifail = 3$: On entry, $sddist = 〈value〉$ and $n = 〈value〉$ .
Constraint: $sddist \geq 4 \times n$ .

$ifail = 4$: On entry, $m = 〈value〉$ .
Constraint: $m > 2$ .

$ifail = 5$: On entry, $n = 〈value〉$ .
Constraint: $n > 2$ .

$ifail = 6$: On entry, $nb = 〈value〉$ .
Constraint: $nb > 0$ .

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.
See Section 7 in the Introduction to the NAG Library FL Interface for further information.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.
See Section 8 in the Introduction to the NAG Library FL Interface for further information.

$ifail = - 999$: Dynamic memory allocation failed.
See Section 9 in the Introduction to the NAG Library FL Interface for further information.

7 Accuracy

Points are moved onto the boundary by bisecting a triangle side nb times. The accuracy is therefore

h \times 2^{- nb}

8 Parallelism and Performance

d03maf is not threaded in any implementation.

9 Further Comments

The time taken is approximately proportional to

m \times n

10 Example

The following program triangulates the circle with centre

(7.0, 7.0)

and radius

6.0

using a basic grid size

h = 4.0

Interfaces: FL CL AD

NAG FL Interface Introduction

D03 (Pde) Chapter Contents

D03 (Pde) Chapter Introduction

d03ma: FL CL AD

NAG FL Interfaced03maf (dim2_​triangulate)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

NAG FL Interface
d03maf (dim2_triangulate)