, it becomes impossible to provide results with any reasonable accuracy (see Section 7), hence the function fails. Such arguments contain insufficient information to determine the phase of oscillation of

J_{1} (x)

; only the amplitude,

\sqrt{\frac{2}{π |x|}}

, can be determined and this is returned on failure. The range for which this occurs is roughly related to machine precision; the function will fail if

|x| ≳ 1 / machine precision

(see the Users' Note for your implementation for details).

4 References

NIST Digital Library of Mathematical Functions

Clenshaw C W (1962) Chebyshev Series for Mathematical Functions Mathematical tables HMSO

5 Arguments

1: $x$ – double Input: On entry: the argument $x$ of the function.
2: $fail$ – NagError * Input/Output: The NAG error argument (see Section 7 in the Introduction to the NAG Library CL Interface).

6 Error Indicators and Warnings

NE_ALLOC_FAIL: Dynamic memory allocation failed.
See Section 3.1.2 in the Introduction to the NAG Library CL Interface for further information.
NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.
See Section 7.5 in the Introduction to the NAG Library CL Interface for further information.
NE_NO_LICENCE: Your licence key may have expired or may not have been installed correctly.
See Section 8 in the Introduction to the NAG Library CL Interface for further information.
NE_REAL_ARG_GT: On entry, $x = 〈value〉$ .
Constraint: $|x| \leq 〈value〉$ .
$|x|$ is too large, the function returns the amplitude of the $J_{1}$ oscillation, $\sqrt{2 / (π |x|)}$ .

7 Accuracy

Let

δ

be the relative error in the argument and

E

be the absolute error in the result. (Since

J_{1} (x)

oscillates about zero, absolute error and not relative error is significant.)

δ

is somewhat larger than machine precision (e.g., if

δ

is due to data errors etc.), then

E

and

δ

are approximately related by:

E ≃ |x J_{0} (x) - J_{1} (x)| δ

(provided

E

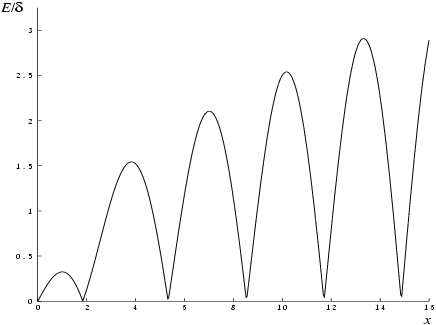
is also within machine bounds). Figure 1 displays the behaviour of the amplification factor

|x J_{0} (x) - J_{1} (x)|

However, if

δ

is of the same order as machine precision, then rounding errors could make

E

slightly larger than the above relation predicts.

For very large

x

, the above relation ceases to apply. In this region,

J_{1} (x) ≃ \sqrt{\frac{2}{π |x|}} \cos (x - \frac{3 π}{4})

. The amplitude

\sqrt{\frac{2}{π |x|}}

can be calculated with reasonable accuracy for all

x

, but

\cos (x - \frac{3 π}{4})

cannot. If

x - \frac{3 π}{4}

is written as

2 N π + θ

where

N

is an integer and

0 \leq θ < 2 π

, then

\cos (x - \frac{3 π}{4})

is determined by

θ

only. If

x ≳ δ^{- 1}

θ

cannot be determined with any accuracy at all. Thus if

x

is greater than, or of the order of, the reciprocal of machine precision, it is impossible to calculate the phase of

J_{1} (x)

and the function must fail.

Figure 1

8 Parallelism and Performance

s17afc is not threaded in any implementation.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

Interfaces: FL CL AD

NAG CL Interface Introduction

S (Specfun) Chapter Contents

S (Specfun) Chapter Introduction

s17af: FL CL AD

NAG CL Interfaces17afc (bessel_​j1_​real)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

NAG CL Interface
s17afc (bessel_j1_real)