NAG CL Interface
s15adc (erfc_​real)

s15adc returns the value of the complementary error function, $\mathrm{erfc}\left(x\right)$.

The function may be called by the names: s15adc, nag_specfun_erfc_real or nag_erfc.

s15adc calculates an approximate value for the complement of the error function

Let $\hat{x}$ be the root of the equation $\mathrm{erfc}\left(x\right)-\mathrm{erf}\left(x\right)=0$ (then $\hat{x}\approx 0.46875$). For $\left|x\right|\le \hat{x}$ the value of $\mathrm{erfc}\left(x\right)$ is based on the following rational Chebyshev expansion for $\mathrm{erf}\left(x\right)$: where $R_{\ell ,m}$ denotes a rational function of degree $\ell$ in the numerator and $m$ in the denominator.

For $\left|x\right|>\hat{x}$ the value of $\mathrm{erfc}\left(x\right)$ is based on a rational Chebyshev expansion for $\mathrm{erfc}\left(x\right)$: for $\hat{x}<\left|x\right|\le 4$ the value is based on the expansion and for $\left|x\right|>4$ it is based on the expansion For each expansion, the specific values of $\ell$ and $m$ are selected to be minimal such that the maximum relative error in the expansion is of the order ${10}^{-d}$, where $d$ is the maximum number of decimal digits that can be accurately represented for the particular implementation (see X02BEC).

For $\left|x\right|\ge x_{\mathrm{hi}}$ there is a danger of setting underflow in $\mathrm{erfc}\left(x\right)$ (the value of $x_{\mathrm{hi}}$ is given in the Users' Note for your implementation). For $x\ge x_{\mathrm{hi}}$, s15adc returns $\mathrm{erfc}\left(x\right)=0$; for $x\le -x_{\mathrm{hi}}$ it returns $\mathrm{erfc}\left(x\right)=2$.

Cody W J (1969) Rational Chebyshev approximations for the error function Math.Comp. 23 631–637

None.

If $\delta$ and $\epsilon$ are relative errors in the argument and result, respectively, then in principle That is, the relative error in the argument, $x$, is amplified by a factor $\frac{2x{e}^{-x^2}}{\sqrt{\pi }\mathrm{erfc}\left(x\right)}$ in the result.

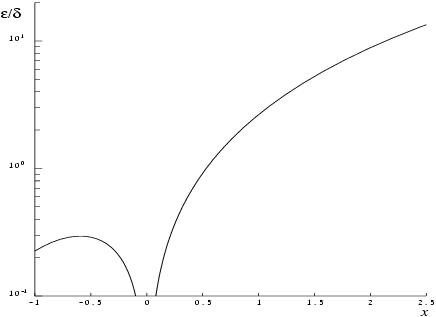
The behaviour of this factor is shown in Figure 1.

It should be noted that near $x=0$ this factor behaves as $\frac{2x}{\sqrt{\pi }}$ and hence the accuracy is largely determined by the machine precision. Also, for large negative $x$, where the factor is $\sim \frac{x{e}^{-x^2}}{\sqrt{\pi }}$, accuracy is mainly limited by machine precision. However, for large positive $x$, the factor becomes $\sim 2x^2$ and to an extent relative accuracy is necessarily lost. The absolute accuracy $E$ is given by so absolute accuracy is guaranteed for all $x$.

s15adc is not threaded in any implementation.

None.

This example reads values of the argument $x$ from a file, evaluates the function at each value of $x$ and prints the results.