for $0 < x \leq 1 / 2$ ,
$\ln Γ (x) \approx - \ln (x) + x R_{n, m}^{1} (x + 1);$
for $1 / 2 < x \leq 3 / 2$ ,
$\ln Γ (x) \approx (x - 1) R_{n, m}^{1} (x);$
for $3 / 2 < x \leq 4$ ,
$\ln Γ (x) \approx (x - 2) R_{n, m}^{2} (x);$
for $4 < x \leq 12$ ,
$\ln Γ (x) \approx R_{n, m}^{3} (x);$
and for $12 < x$ ,
$\ln Γ (x) \approx (x - \frac{1}{2}) \ln (x) - x + \ln (\sqrt{2 π}) + \frac{1}{x} R_{n, m}^{4} (1 / x^{2}) .$ (1)

For each expansion, the specific values of

n

and

m

are selected to be minimal such that the maximum relative error in the expansion is of the order

10^{- d}

, where

d

is the maximum number of decimal digits that can be accurately represented for the particular implementation (see X02BEC).

Let

ε

denote machine precision and let

x_{huge}

denote the largest positive model number (see X02ALC). For

x < 0.0

the value

\ln Γ (x)

is not defined; s14apc returns zero and exits with

fail . code =

NW_IVALID. It also exits with

fail . code =

NW_IVALID when

x = 0.0

, and in this case the value

x_{huge}

is returned. For

x

in the interval

(0.0, ε]

, the function

\ln Γ (x) = - \ln (x)

to machine accuracy.

Now denote by

x_{big}

the largest allowable argument for

\ln Γ (x)

on the machine. For

{(x_{big})}^{1 / 4} < x \leq x_{big}

the

R_{n, m}^{4} (1 / x^{2})

term in Equation (1) is negligible. For

x > x_{big}

there is a danger of setting overflow, and so s14apc exits with

fail . code =

NE_INT and returns

x_{huge}

. The value of

x_{big}

is given in the Users' Note for your implementation.

4 References

NIST Digital Library of Mathematical Functions

Cody W J and Hillstrom K E (1967) Chebyshev approximations for the natural logarithm of the gamma function Math.Comp. 21 198–203

5 Arguments

1: $n$ – Integer Input

On entry:

n

, the number of points.

Constraint:

n \geq 0

2: $x [n]$ – const double Input

On entry: the argument

x_{i}

of the function, for

i = 1, 2, \dots, n

Constraint:

x [i - 1] > 0

, for

i = 1, 2, \dots, n

3: $f [n]$ – double Output

On exit:

\ln Γ (x_{i})

, the function values.

4: $ivalid [n]$ – Integer Output

On exit:

ivalid [i - 1]

contains the error code for

x_{i}

, for

i = 1, 2, \dots, n

$ivalid [i - 1] = 0$: No error.
$ivalid [i - 1] = 1$: $x_{i} \leq 0$ .
$ivalid [i - 1] = 2$: $x_{i}$ is too large and positive. The threshold value is the same as for $fail . code =$ NE_REAL_ARG_GT in s14abc, as defined in the Users' Note for your implementation.

5: $fail$ – NagError * Input/Output

The NAG error argument (see Section 7 in the Introduction to the NAG Library CL Interface).

6 Error Indicators and Warnings

NE_ALLOC_FAIL: Dynamic memory allocation failed.
See Section 3.1.2 in the Introduction to the NAG Library CL Interface for further information.
NE_BAD_PARAM: On entry, argument $〈value〉$ had an illegal value.
NE_INT: On entry, $n = 〈value〉$ .
Constraint: $n \geq 0$ .
NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.
See Section 7.5 in the Introduction to the NAG Library CL Interface for further information.
NE_NO_LICENCE: Your licence key may have expired or may not have been installed correctly.
See Section 8 in the Introduction to the NAG Library CL Interface for further information.
NW_IVALID: On entry, at least one value of x was invalid.
Check ivalid for more information.

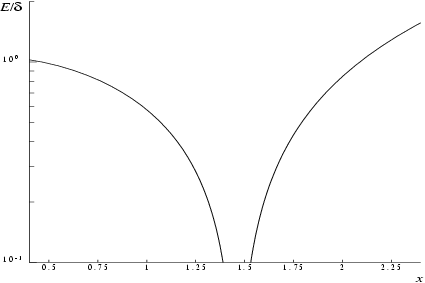
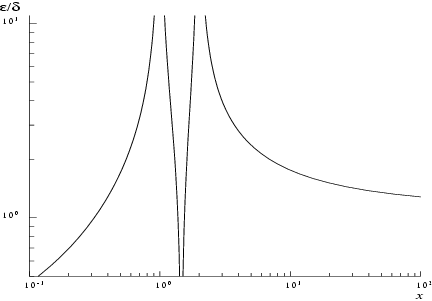
7 Accuracy

Let

δ

and

ε

be the relative errors in the argument and result respectively, and

E

be the absolute error in the result.

δ

is somewhat larger than machine precision, then

E ≃ |x \times Ψ (x)| δ and ε ≃ |\frac{x \times Ψ (x)}{\ln Γ (x)}| δ

where

Ψ (x)

is the digamma function

\frac{Γ^{'} (x)}{Γ (x)}

. Figure 1 and Figure 2 show the behaviour of these error amplification factors.

Figure 1

Figure 2

These show that relative error can be controlled, since except near

x = 1 or 2

relative error is attenuated by the function or at least is not greatly amplified.

For large

x

ε ≃ (1 + \frac{1}{\ln x}) δ

and for small

x

ε ≃ \frac{1}{\ln x} δ

The function

\ln Γ (x)

has zeros at

x = 1

and

2

and hence relative accuracy is not maintainable near those points. However, absolute accuracy can still be provided near those zeros as is shown above.

If however,

δ

is of the order of machine precision, then rounding errors in the function's internal arithmetic may result in errors which are slightly larger than those predicted by the equalities. It should be noted that even in areas where strong attenuation of errors is predicted the relative precision is bounded by the effective machine precision.

8 Parallelism and Performance

s14apc is not threaded in any implementation.

9 Further Comments

None.

10 Example

This example reads values of x from a file, evaluates the function at each value of

x_{i}

and prints the results.

Interfaces: FL CL AD

NAG CL Interface Introduction

S (Specfun) Chapter Contents

S (Specfun) Chapter Introduction

s14ap: FL CL AD

NAG CL Interfaces14apc (gamma_​log_​real_​vector)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

NAG CL Interface
s14apc (gamma_log_real_vector)