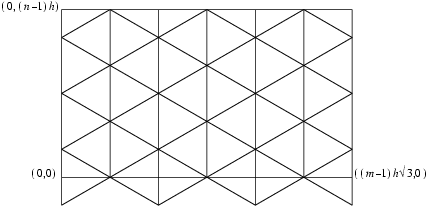
D03MAF places a triangular mesh over a given two-dimensional region. The region may have any shape, including one with holes.
| SUBROUTINE D03MAF ( |
H, M, N, NB, NPTS, PLACES, INDX, SDINDX, ISIN, DIST, SDDIST, IFAIL) |
| INTEGER |
M, N, NB, NPTS, INDX(4,SDINDX), SDINDX, ISIN, SDDIST, IFAIL |
| REAL (KIND=nag_wp) |
H, PLACES(2,SDINDX), DIST(4,SDDIST) |
| EXTERNAL |
ISIN |
|
D03MAF begins with a uniform triangular grid as shown in
Figure 1 and assumes that the region to be triangulated lies within the rectangle given by the inequalities
This rectangle is drawn in bold in
Figure 1. The region is specified by the
ISIN which must determine whether any given point
lies in the region. The uniform grid is processed column-wise, with
preceding
if
or
,
. Points near the boundary are moved onto it and points well outside the boundary are omitted. The direction of movement is chosen to avoid pathologically thin triangles. The points accepted are numbered in exactly the same order as the corresponding points of the uniform grid were scanned. The output consists of the
coordinates of all grid points and integers indicating whether they are internal and to which other points they are joined by triangle sides.
Further details of the algorithm are given in the references.
Reid J K (1970) Fortran subroutines for the solutions of Laplace's equation over a general routine in two dimensions Harwell Report TP422
Reid J K (1972) On the construction and convergence of a finite-element solution of Laplace's equation J. Instr. Math. Appl. 9 1–13
If on entry
or
, explanatory error messages are output on the current error message unit (as defined by
X04AAF).
Points are moved onto the boundary by bisecting a triangle side
NB times. The accuracy is therefore
.
Not applicable.