NAG Library Function Document

nag_bessel_k0 (s18acc)

+− Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

+− 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1 Purpose

nag_bessel_k0 (s18acc) returns the value of the modified Bessel function

K_{0} (x)

2 Specification

#include <nag.h>

#include <nags.h>

double

nag_bessel_k0 (double x, NagError *fail)

3 Description

nag_bessel_k0 (s18acc) evaluates an approximation to the modified Bessel function of the second kind

K_{0} (x)

Note:

K_{0} (x)

is undefined for

x \leq 0

and the function will fail for such arguments.

The function is based on five Chebyshev expansions:

For

0 < x \leq 1

K_{0} (x) = - \ln x \underset{r = 0}{\sum^{'}} a_{r} T_{r} (t) + \underset{r = 0}{\sum^{'}} b_{r} T_{r} (t),   where ​ t = 2 x^{2} - 1 .

For

1 < x \leq 2

K_{0} (x) = e^{- x} \underset{r = 0}{\sum^{'}} c_{r} T_{r} (t),   where ​ t = 2 x - 3 .

For

2 < x \leq 4

K_{0} (x) = e^{- x} \underset{r = 0}{\sum^{'}} d_{r} T_{r} (t),   where ​ t = x - 3 .

For

x > 4

K_{0} (x) = \frac{e^{- x}}{\sqrt{x}} \underset{r = 0}{\sum^{'}} e_{r} T_{r} (t), where ​ t = \frac{9 - x}{1 + x} .

For

x

near zero,

K_{0} (x) ≃ - γ - \ln (\frac{x}{2})

, where

γ

denotes Euler's constant. This approximation is used when

x

is sufficiently small for the result to be correct to machine precision.

For large

x

, where there is a danger of underflow due to the smallness of

K_{0}

, the result is set exactly to zero.

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

5 Arguments

1: x – doubleInput: On entry: the argument $x$ of the function.
Constraint: $x > 0.0$ .
2: fail – NagError *Input/Output: The NAG error argument (see Section 3.6 in the Essential Introduction).

6 Error Indicators and Warnings

NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.
NE_REAL_ARG_LE: On entry, $x = ⟨value⟩$ .
Constraint: $x > 0.0$ .
$K_{0}$ is undefined and the function returns zero.

7 Accuracy

Let

δ

and

ε

be the relative errors in the argument and result respectively.

δ

is somewhat larger than the machine precision (i.e., if

δ

is due to data errors etc.), then

ε

and

δ

are approximately related by:

ε ≃ |\frac{x K_{1} (x)}{K_{0} (x)}| δ .

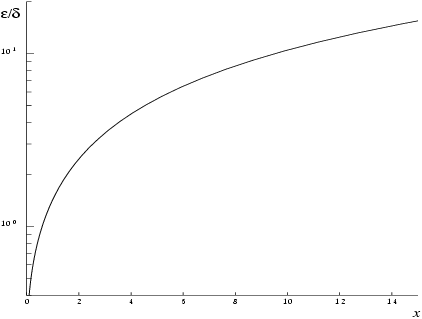
Figure 1 shows the behaviour of the error amplification factor

|\frac{x K_{1} (x)}{K_{0} (x)}| .

However, if

δ

is of the same order as machine precision, then rounding errors could make

ε

slightly larger than the above relation predicts.

For small

x

, the amplification factor is approximately

|\frac{1}{\ln x}|

, which implies strong attenuation of the error, but in general

ε

can never be less than the machine precision.

For large

x

ε ≃ x δ

and we have strong amplification of the relative error. Eventually

K_{0}

, which is asymptotically given by

\frac{e^{- x}}{\sqrt{x}}

, becomes so small that it cannot be calculated without underflow and hence the function will return zero. Note that for large

x

the errors will be dominated by those of the standard math library function exp.

Figure 1

8 Parallelism and Performance

Not applicable.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Function Documentnag_bessel_k0 (s18acc)