NAG Library Function Document

nag_mesh2d_join (d06dbc)

nag_mesh2d_join (double eps, Integer nv1, Integer nelt1, Integer nedge1, const double coor1[], const Integer edge1[], const Integer conn1[], const Integer reft1[], Integer nv2, Integer nelt2, Integer nedge2, const double coor2[], const Integer edge2[], const Integer conn2[], const Integer reft2[], Integer *nv3, Integer *nelt3, Integer *nedge3, double coor3[], Integer edge3[], Integer conn3[], Integer reft3[], Integer itrace, const char *outfile, NagError *fail)

3 Description

nag_mesh2d_join (d06dbc) joins together two adjacent, or overlapping, meshes. If the two meshes are adjacent then vertices belonging to the part of the boundary forming the common interface should coincide. If the two meshes overlap then vertices and triangles in the overlapping zone should coincide too.

This function is partly derived from material in the MODULEF package from INRIA (Institut National de Recherche en Informatique et Automatique).

4 References

None.

5 Arguments

1: eps – doubleInput

On entry: the relative precision of the restitching of the two input meshes (see Section 9).

Suggested value:

0.001

Constraint:

eps > 0.0

2: nv1 – IntegerInput

On entry: the total number of vertices in the first input mesh.

Constraint:

nv1 \geq 3

3: nelt1 – IntegerInput

On entry: the number of triangular elements in the first input mesh.

Constraint:

nelt1 \leq 2 \times nv1 - 1

4: nedge1 – IntegerInput

On entry: the number of boundary edges in the first input mesh.

Constraint:

nedge1 \geq 1

5: coor1[ $2 \times nv1$ ] – const doubleInput

Note: the

(i, j)

th element of the matrix is stored in

coor1 [(j - 1) \times 2 + i - 1]

On entry:

coor1 [(i - 1) \times 2]

contains the

x

coordinate of the

i

th vertex of the first input mesh, for

i = 1, 2, \dots, nv1

; while

coor1 [(i - 1) \times 2 + 1]

contains the corresponding

y

coordinate.

6: edge1[ $3 \times nedge1$ ] – const IntegerInput

Note: the

(i, j)

th element of the matrix is stored in

edge1 [(j - 1) \times 3 + i - 1]

On entry: the specification of the boundary edges of the first input mesh.

edge1 [(j - 1) \times 3]

and

edge1 [(j - 1) \times 3 + 1]

contain the vertex numbers of the two end points of the

j

th boundary edge.

edge1 [(j - 1) \times 3 + 2]

is a user-supplied tag for the

j

th boundary edge.

Constraint:

1 \leq edge1 [(j - 1) \times 3 + i - 1] \leq nv1

and

edge1 [(j - 1) \times 3] \neq edge1 [(j - 1) \times 3 + 1]

, for

i = 1, 2

and

j = 1, 2, \dots, nedge1

7: conn1[ $3 \times nelt1$ ] – const IntegerInput

Note: the

(i, j)

th element of the matrix is stored in

conn1 [(j - 1) \times 3 + i - 1]

On entry: the connectivity between triangles and vertices of the first input mesh. For each triangle

j

conn1 [(j - 1) \times 3 + i - 1]

gives the indices of its three vertices (in anticlockwise order), for

i = 1, 2, 3

and

j = 1, 2, \dots, nelt1

Constraints:

$1 \leq conn1 [(j - 1) \times 3 + i - 1] \leq nv1$ ;
$conn1 [(j - 1) \times 3] \neq conn1 [(j - 1) \times 3 + 1]$ ;
$conn1 [(j - 1) \times 3] \neq conn1 [(j - 1) \times 3 + 2]$ and
$conn1 [(j - 1) \times 3 + 1] \neq conn1 [(j - 1) \times 3 + 2]$ , for $i = 1, 2, 3$ and $j = 1, 2, \dots, nelt1$ .

8: reft1[nelt1] – const IntegerInput

On entry:

reft1 [k - 1]

contains the user-supplied tag of the

k

th triangle from the first input mesh, for

k = 1, 2, \dots, nelt1

9: nv2 – IntegerInput

On entry: the total number of vertices in the second input mesh.

Constraint:

nv2 \geq 3

10: nelt2 – IntegerInput

On entry: the number of triangular elements in the second input mesh.

Constraint:

nelt2 \leq 2 \times nv2 - 1

11: nedge2 – IntegerInput

On entry: the number of boundary edges in the second input mesh.

Constraint:

nedge2 \geq 1

12: coor2[ $2 \times nv2$ ] – const doubleInput

Note: the

(i, j)

th element of the matrix is stored in

coor2 [(j - 1) \times 2 + i - 1]

On entry:

coor2 [(i - 1) \times 2]

contains the

x

coordinate of the

i

th vertex of the second input mesh, for

i = 1, 2, \dots, nv2

; while

coor2 [(i - 1) \times 2 + 1]

contains the corresponding

y

coordinate.

13: edge2[ $3 \times nedge2$ ] – const IntegerInput

Note: the

(i, j)

th element of the matrix is stored in

edge2 [(j - 1) \times 3 + i - 1]

On entry: the specification of the boundary edges of the second input mesh.

edge2 [(j - 1) \times 3]

and

edge2 [(j - 1) \times 3 + 1]

contain the vertex numbers of the two end points of the

j

th boundary edge.

edge2 [(j - 1) \times 3 + 2]

is a user-supplied tag for the

j

th boundary edge.

Constraint:

1 \leq edge2 [(j - 1) \times 3 + i - 1] \leq nv2

and

edge2 [(j - 1) \times 3] \neq edge2 [(j - 1) \times 3 + 1]

, for

i = 1, 2

and

j = 1, 2, \dots, nedge2

14: conn2[ $3 \times nelt2$ ] – const IntegerInput

Note: the

(i, j)

th element of the matrix is stored in

conn2 [(j - 1) \times 3 + i - 1]

On entry: the connectivity between triangles and vertices of the second input mesh. For each triangle

j

conn2 [(j - 1) \times 3 + i - 1]

gives the indices of its three vertices (in anticlockwise order), for

i = 1, 2, 3

and

j = 1, 2, \dots, nelt2

Constraints:

$1 \leq conn2 [(j - 1) \times 3 + i - 1] \leq nv2$ ;
$conn2 [(j - 1) \times 3] \neq conn2 [(j - 1) \times 3 + 1]$ ;
$conn2 [(j - 1) \times 3] \neq conn2 [(j - 1) \times 3 + 2]$ and
$conn2 [(j - 1) \times 3 + 1] \neq conn2 [(j - 1) \times 3 + 2]$ , for $i = 1, 2, 3$ and $j = 1, 2, \dots, nelt2$ .

15: reft2[nelt2] – const IntegerInput

On entry:

reft2 [k - 1]

contains the user-supplied tag of the

k

th triangle from the second input mesh, for

k = 1, 2, \dots, nelt2

16: nv3 – Integer *Output

On exit: the total number of vertices in the resulting mesh.

17: nelt3 – Integer *Output

On exit: the number of triangular elements in the resulting mesh.

18: nedge3 – Integer *Output

On exit: the number of boundary edges in the resulting mesh.

19: coor3[ $\dim$ ] – doubleOutput

Note: the dimension, dim, of the array coor3 must be at least

2 \times (nv1 + nv2)

The

(i, j)

th element of the matrix is stored in

coor3 [(j - 1) \times 2 + i - 1]

On exit:

coor3 [(i - 1) \times 2]

will contain the

x

coordinate of the

i

th vertex of the resulting mesh, for

i = 1, 2, \dots, nv3

; while

coor3 [(i - 1) \times 2 + 1]

will contain the corresponding

y

coordinate.

20: edge3[ $\dim$ ] – IntegerOutput

Note: the dimension, dim, of the array edge3 must be at least

3 \times (nedge1 + nedge2)

. This may be reduced to

nedge3

once that value is known.

The

(i, j)

th element of the matrix is stored in

edge3 [(j - 1) \times 3 + i - 1]

On exit: the specification of the boundary edges of the resulting mesh.

edge3 [(j - 1) \times 3 + i - 1]

will contain the vertex number of the

i

th end point (

i = 1, 2

) of the

j

th boundary or interface edge.

If the two meshes overlap,

edge3 [(j - 1) \times 3 + 2]

will contain the same tag as the corresponding edge belonging to the first and/or the second input mesh.

If the two meshes are adjacent,

(i)	if the $j$ th edge is part of the partition interface, then $edge3 [(j - 1) \times 3 + 2]$ will contain the value $1000 \times k_{1} + k_{2}$ where $k_{1}$ and $k_{2}$ are the tags for the same edge of the first and the second mesh respectively;
(ii)	otherwise, $edge3 [(j - 1) \times 3 + 2]$ will contain the same tag as the corresponding edge belonging to the first and/or the second input mesh.

21: conn3[ $\dim$ ] – IntegerOutput

Note: the dimension, dim, of the array conn3 must be at least

3 \times (nelt1 + nelt2)

. This may be reduced to

nelt3

once that value is known.

The

(i, j)

th element of the matrix is stored in

conn3 [(j - 1) \times 3 + i - 1]

On exit: the connectivity between triangles and vertices of the resulting mesh.

conn3 [(j - 1) \times 3 + i - 1]

will give the indices of its three vertices (in anticlockwise order), for

i = 1, 2, 3

and

j = 1, 2, \dots, nelt3

22: reft3[ $\dim$ ] – IntegerOutput

Note: the dimension, dim, of the array reft3 must be at least

nelt1 + nelt2

. This may be reduced to

nelt3

once that value is known.

On exit: if the two meshes form a partition,

reft3 [k - 1]

will contain the same tag as the corresponding triangle belonging to the first or the second input mesh, for

k = 1, 2, \dots, nelt3

. If the two meshes overlap, then

reft3 [k - 1]

will contain the value

1000 \times k_{1} + k_{2}

where

k_{1}

and

k_{2}

are the user-supplied tags for the same triangle of the first and the second mesh respectively, for

k = 1, 2, \dots, nelt3

23: itrace – IntegerInput

On entry: the level of trace information required from nag_mesh2d_join (d06dbc).

$itrace \leq 0$: No output is generated.
$itrace \geq 1$: Details about the common vertices, edges and triangles to both meshes are printed.

24: outfile – const char *Input

On entry: the name of a file to which diagnostic output will be directed. If outfile is NULL the diagnostic output will be directed to standard output.

25: fail – NagError *Input/Output

The NAG error argument (see Section 3.6 in the Essential Introduction).

6 Error Indicators and Warnings

NE_ALLOC_FAIL: Dynamic memory allocation failed.
NE_BAD_PARAM: On entry, argument $⟨value⟩$ had an illegal value.
NE_INT: On entry, $nedge1 = ⟨value⟩$ .
Constraint: $nedge1 \geq 1$ .
On entry, $nedge2 = ⟨value⟩$ .
Constraint: $nedge2 \geq 1$ .
On entry, $nv1 = ⟨value⟩$ .
Constraint: $nv1 \geq 3$ .
On entry, $nv2 = ⟨value⟩$ .
Constraint: $nv2 \geq 3$ .
NE_INT_2: On entry, $nelt1 = ⟨value⟩$ and $nv1 = ⟨value⟩$ .
Constraint: $nelt1 \leq 2 \times nv1 - 1$ .
On entry, $nelt2 = ⟨value⟩$ and $nv2 = ⟨value⟩$ .
Constraint: $nelt2 \leq 2 \times nv2 - 1$ .
On entry, the endpoints of edge $J$ in the first mesh have the same index $I$ : $J = ⟨value⟩$ and $I = ⟨value⟩$ .
On entry, the endpoints of edge $J$ in the second mesh have the same index $I$ : $J = ⟨value⟩$ and $I = ⟨value⟩$ .
On entry, vertices $1$ and $2$ of triangle $K$ in the first mesh have the same index $I$ : $K = ⟨value⟩$ and $I = ⟨value⟩$ .
On entry, vertices $1$ and $2$ of triangle $K$ in the second mesh have the same index $I$ : $K = ⟨value⟩$ and $I = ⟨value⟩$ .
On entry, vertices $1$ and $3$ of triangle $K$ in the first mesh have the same index $I$ : $K = ⟨value⟩$ and $I = ⟨value⟩$ .
On entry, vertices $1$ and $3$ of triangle $K$ in the second mesh have the same index $I$ : $K = ⟨value⟩$ and $I = ⟨value⟩$ .
On entry, vertices $2$ and $3$ of triangle $K$ in the first mesh have the same index $I$ : $K = ⟨value⟩$ and $I = ⟨value⟩$ .
On entry, vertices $2$ and $3$ of triangle $K$ in the second mesh have the same index $I$ : $K = ⟨value⟩$ and $I = ⟨value⟩$ .
NE_INT_4: On entry, $CONN1 (I, J) = ⟨value⟩$ , $I = ⟨value⟩$ , $J = ⟨value⟩$ and $nv1 = ⟨value⟩$ .
Constraint: $CONN1 (I, J) \geq 1$ and $CONN1 (I, J) \leq nv1$ , where $CONN1 (I, J)$ denotes $conn1 [(J - 1) \times 3 + I - 1]$ .
On entry, $CONN2 (I, J) = ⟨value⟩$ , $I = ⟨value⟩$ , $J = ⟨value⟩$ and $nv2 = ⟨value⟩$ .
Constraint: $CONN2 (I, J) \geq 1$ and $CONN2 (I, J) \leq nv2$ , where $CONN2 (I, J)$ denotes $conn2 [(J - 1) \times 3 + I - 1]$ .
On entry, $EDGE1 (I, J) = ⟨value⟩$ , $I = ⟨value⟩$ , $J = ⟨value⟩$ and $nv1 = ⟨value⟩$ .
Constraint: $EDGE1 (I, J) \geq 1$ and $EDGE1 (I, J) \leq nv1$ , where $EDGE1 (I, J)$ denotes $edge1 [(J - 1) \times 3 + I - 1]$ .
On entry, $EDGE2 (I, J) = ⟨value⟩$ , $I = ⟨value⟩$ , $J = ⟨value⟩$ and $nv2 = ⟨value⟩$ .
Constraint: $EDGE2 (I, J) \geq 1$ and $EDGE2 (I, J) \leq nv2$ , where $EDGE2 (I, J)$ denotes $edge2 [(J - 1) \times 3 + I - 1]$ .
NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.
NE_MESH_ERROR: A serious error has occurred in an internal call to the restitching routine. Check the input of the two meshes, especially the edges/vertices and/or the triangles/vertices connectivities. Seek expert help.
The function has detected a different number of coincident edges from the two meshes on the partition interface $⟨value⟩$ $⟨value⟩$ . Check the input of the two meshes, especially the edges/vertices connectivity.
The function has detected a different number of coincident triangles from the two meshes in the overlapping zone $⟨value⟩$ $⟨value⟩$ . Check the input of the two meshes, especially the triangles/vertices connectivity.
The function has detected only $⟨value⟩$ coincident vertices with a precision $eps = ⟨value⟩$ . Either eps should be changed or the two meshes are not restitchable.
NE_NOT_CLOSE_FILE: Cannot close file $⟨value⟩$ .
NE_NOT_WRITE_FILE: Cannot open file $⟨value⟩$ for writing.
NE_REAL: On entry, $eps = ⟨value⟩$ .
Constraint: $eps > 0.0$ .

7 Accuracy

Not applicable.

8 Parallelism and Performance

Not applicable.

9 Further Comments

nag_mesh2d_join (d06dbc) finds all the common vertices between the two input meshes using the relative precision of the restitching argument eps. You are advised to vary the value of eps in the neighbourhood of

0.001

with

itrace \geq 1

to get the optimal value for the meshes under consideration.

10 Example

For this function two examples are presented. There is a single example program for nag_mesh2d_join (d06dbc), with a main program and the code to solve the two example problems given in Example 1 (ex1) and Example 2 (ex2).

Example 1 (ex1)

This example involves the unit square

{[0, 1]}^{2}

meshed uniformly, and then translated by a vector

\vec{u} = (\begin{matrix} u_{1} \\ u_{2} \end{matrix})

(using nag_mesh2d_trans (d06dac)). This translated mesh is then restitched with the original mesh. Two cases are considered:

(a)	overlapping meshes ( $u_{1} = 15.0$ , $u_{2} = 17.0$ ),
(b)	partitioned meshes ( $u_{1} = 19.0$ , $u_{2} = 0.0$ ).

The mesh on the unit square has

400

vertices,

722

triangles and its boundary has

76

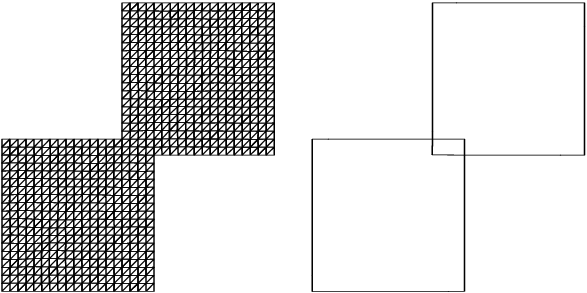
edges. In the overlapping case the resulting geometry is shown in Figure 1 and Figure 2. The resulting geometry for the partitioned meshes is shown in Figure 3.

Example 2 (ex2)

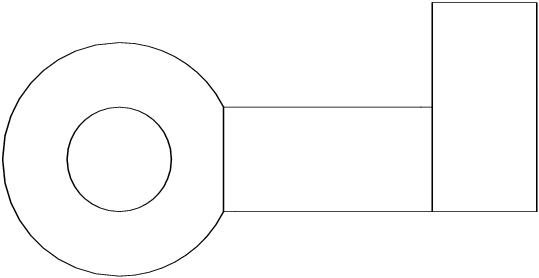
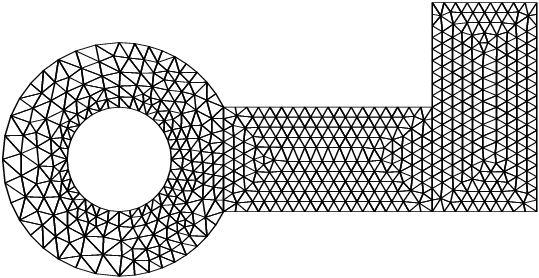
This example restitches three geometries by calling the function nag_mesh2d_join (d06dbc) twice. The result is a mesh with three partitions. The first geometry is meshed by the Delaunay–Voronoi process (using nag_mesh2d_delaunay (d06abc)), the second one meshed by an Advancing Front algorithm (using nag_mesh2d_front (d06acc)), while the third one is the result of a rotation (by