NAG Library Function Document

nag_mesh2d_delaunay (d06abc)

void	nag_mesh2d_delaunay (Integer nvb, Integer nvint, Integer nvmax, Integer nedge, const Integer edge[], Integer nv, Integer nelt, double coor[], Integer conn[], const double weight[], Integer npropa, Integer itrace, const char outfile, NagError fail)

3 Description

nag_mesh2d_delaunay (d06abc) generates the set of interior vertices using a Delaunay–Voronoi process, based on an incremental method. It allows you to specify a number of fixed interior mesh vertices together with weights which allow concentration of the mesh in their neighbourhood. For more details about the triangulation method, consult the d06 Chapter Introduction as well as George and Borouchaki (1998).

This function is derived from material in the MODULEF package from INRIA (Institut National de Recherche en Informatique et Automatique).

4 References

George P L and Borouchaki H (1998) Delaunay Triangulation and Meshing: Application to Finite Elements Editions HERMES, Paris

5 Arguments

1: nvb – IntegerInput

On entry: the number of vertices in the input boundary mesh.

Constraint:

nvb \geq 3

2: nvint – IntegerInput

On entry: the number of fixed interior mesh vertices to which a weight will be applied.

Constraint:

nvint \geq 0

3: nvmax – IntegerInput

On entry: the maximum number of vertices in the mesh to be generated.

Constraint:

nvmax \geq nvb + nvint

4: nedge – IntegerInput

On entry: the number of boundary edges in the input mesh.

Constraint:

nedge \geq 1

5: edge[ $3 \times nedge$ ] – const IntegerInput

Note: the

(i, j)

th element of the matrix is stored in

edge [(j - 1) \times 3 + i - 1]

On entry: the specification of the boundary edges.

edge [(j - 1) \times 3]

and

edge [(j - 1) \times 3 + 1]

contain the vertex numbers of the two end points of the

j

th boundary edge.

edge [(j - 1) \times 3 + 2]

is a user-supplied tag for the

j

th boundary edge and is not used by nag_mesh2d_delaunay (d06abc). Note that the edge vertices are numbered from

1

to nvb.

Constraint:

1 \leq edge [(j - 1) \times 3 + i - 1] \leq nvb

and

edge [(j - 1) \times 3] \neq edge [(j - 1) \times 3 + 1]

, for

i = 1, 2

and

j = 1, 2, \dots, nedge

6: nv – Integer *Output

On exit: the total number of vertices in the output mesh (including both boundary and interior vertices). If

nvb + nvint = nvmax

, no interior vertices will be generated and

nv = nvmax

7: nelt – Integer *Output

On exit: the number of triangular elements in the mesh.

8: coor[ $2 \times nvmax$ ] – doubleInput/Output

Note: the

(i, j)

th element of the matrix is stored in

coor [(j - 1) \times 2 + i - 1]

On entry:

coor [(i - 1) \times 2]

contains the

x

coordinate of the

i

th input boundary mesh vertex, for

i = 1, 2, \dots, nvb

coor [(i - 1) \times 2]

contains the

x

coordinate of the

(i - nvb)

th fixed interior vertex, for

i = nvb + 1, \dots, nvb + nvint

. For boundary and interior vertices,

coor [(i - 1) \times 2 + 1]

contains the corresponding

y

coordinate, for

i = 1, 2, \dots, nvb + nvint

On exit:

coor [(i - 1) \times 2]

will contain the

x

coordinate of the

(i - nvb - nvint)

th generated interior mesh vertex, for

i = nvb + nvint + 1, \dots, nv

; while

coor [(i - 1) \times 2 + 1]

will contain the corresponding

y

coordinate. The remaining elements are unchanged.

9: conn[ $3 \times (2 \times nvmax + 5)$ ] – IntegerOutput

Note: the

(i, j)

th element of the matrix is stored in

conn [(j - 1) \times 3 + i - 1]

On exit: the connectivity of the mesh between triangles and vertices. For each triangle

j

conn [(j - 1) \times 3 + i - 1]

gives the indices of its three vertices (in anticlockwise order), for

i = 1, 2, 3

and

j = 1, 2, \dots, nelt

. Note that the mesh vertices are numbered from

1

to nv.

10: weight[ $\dim$ ] – const doubleInput

Note: the dimension, dim, of the array weight must be at least

\max (1, nvint)

On entry: the weight of fixed interior vertices. It is the diameter of triangles (length of the longer edge) created around each of the given interior vertices.

Constraint: if

nvint > 0

weight [i - 1] > 0.0

, for

i = 1, 2, \dots, nvint

11: npropa – IntegerInput

On entry: the propagation type and coefficient, the argument npropa is used when the internal points are created. They are distributed in a geometric manner if npropa is positive and in an arithmetic manner if it is negative. For more details see Section 9.

Constraint:

npropa \neq 0

12: itrace – IntegerInput

On entry: the level of trace information required from nag_mesh2d_delaunay (d06abc).

$itrace \leq 0$: No output is generated.
$itrace \geq 1$: Output from the meshing solver is printed. This output contains details of the vertices and triangles generated by the process.

You are advised to set

itrace = 0

, unless you are experienced with finite element mesh generation.

13: outfile – const char *Input

On entry: the name of a file to which diagnostic output will be directed. If outfile is NULL the diagnostic output will be directed to standard output.

14: fail – NagError *Input/Output

The NAG error argument (see Section 3.6 in the Essential Introduction).

6 Error Indicators and Warnings

NE_ALLOC_FAIL: Dynamic memory allocation failed.
NE_BAD_PARAM: On entry, argument $⟨value⟩$ had an illegal value.
NE_INT: On entry, $nedge = ⟨value⟩$ .
Constraint: $nedge \geq 1$ .
On entry, $npropa = 0$ .
On entry, $nvb = ⟨value⟩$ .
Constraint: $nvb \geq 3$ .
On entry, $nvint = ⟨value⟩$ .
Constraint: $nvint \geq 0$ .
NE_INT_2: On entry, the endpoints of the edge $J$ have the same index $I$ : $J = ⟨value⟩$ and $I = ⟨value⟩$ .
NE_INT_3: On entry, $nvb = ⟨value⟩$ , $nvint = ⟨value⟩$ and $nvmax = ⟨value⟩$ .
Constraint: $nvmax \geq nvb + nvint$ .
NE_INT_4: On entry, $EDGE (I, J) = ⟨value⟩$ , $I = ⟨value⟩$ , $J = ⟨value⟩$ and $nvb = ⟨value⟩$ .
Constraint: $EDGE (I, J) \geq 1$ and $EDGE (I, J) \leq nvb$ , where $EDGE (I, J)$ denotes $edge [(J - 1) \times 3 + I - 1]$ .
NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.
NE_MESH_ERROR: An error has occurred during the generation of the boundary mesh. It appears that nvmax is not large enough: $nvmax = ⟨value⟩$ .
An error has occurred during the generation of the interior mesh. Check the inputs of the boundary.
NE_NOT_CLOSE_FILE: Cannot close file $⟨value⟩$ .
NE_NOT_WRITE_FILE: Cannot open file $⟨value⟩$ for writing.
NE_REAL_ARRAY_INPUT: On entry, $weight [I - 1] = ⟨value⟩$ and $I = ⟨value⟩$ .
Constraint: $weight [I - 1] > 0.0$ .

7 Accuracy

Not applicable.

8 Parallelism and Performance

nag_mesh2d_delaunay (d06abc) is not threaded by NAG in any implementation.

nag_mesh2d_delaunay (d06abc) makes calls to BLAS and/or LAPACK routines, which may be threaded within the vendor library used by this implementation. Consult the documentation for the vendor library for further information.

Please consult the Users' Note for your implementation for any additional implementation-specific information.

9 Further Comments

The position of the internal vertices is a function position of the vertices on the given boundary. A fine mesh on the boundary results in a fine mesh in the interior. To dilute the influence of the data on the interior of the domain, the value of npropa can be changed. The propagation coefficient is calculated as:

ω = 1 + \frac{a - 1.0}{20.0}

, where

a

is the absolute value of npropa. During the process vertices are generated on edges of the mesh

T_{i}

to obtain the mesh

T_{i + 1}

in the general incremental method (consult the d06 Chapter Introduction or George and Borouchaki (1998)). This generation uses the coefficient

ω

, and it is geometric if

npropa > 0

, and arithmetic otherwise. But increasing the value of

a

may lead to failure of the process, due to precision, especially in geometries with holes. So you are advised to manipulate the argument npropa with care.

You are advised to take care to set the boundary inputs properly, especially for a boundary with multiply connected components. The orientation of the interior boundaries should be in clockwise order and opposite to that of the exterior boundary. If the boundary has only one connected component, its orientation should be anticlockwise.

10 Example

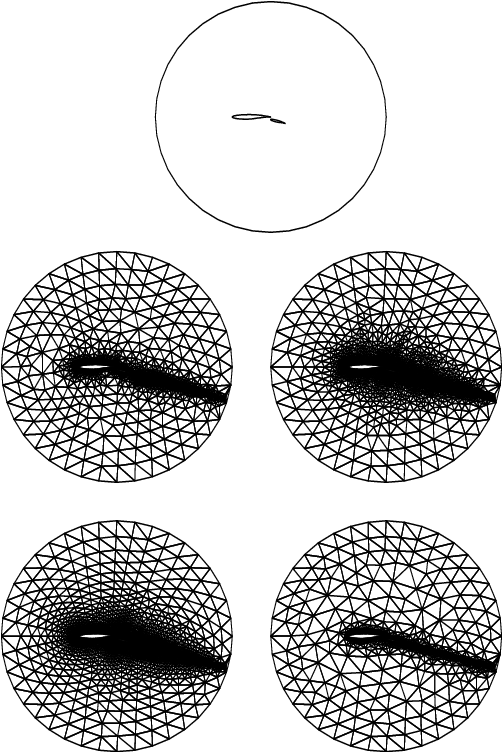
In this example, a geometry with two holes (two wings inside an exterior circle) is meshed using a Delaunay–Voronoi method. The exterior circle is centred at the point

(1.0, 0.0)

with a radius

3

, the first RAE wing begins at the origin and it is normalized, and the last wing is a result from the first one after a translation, a scale reduction and a rotation. To be able to carry out some realistic computation on that geometry, some interior points have been introduced to have a finer mesh in the wake of those airfoils.

The boundary mesh has

296

vertices and

296

edges (see Figure 1 top). Note that the particular mesh generated could be sensitive to the machine precision and therefore may differ from one implementation to another. The interior meshes for different values of npropa are given in Figure 1.

Figure 1: The boundary mesh (top), the interior mesh with $npropa = - 5$ (middle left), $- 1$ (middle right),
$1$ (bottom left) and $5$ (bottom right) of a double RAE wings inside a circle geometry

nag_mesh2d_delaunay (d06abc) (PDF version)

d06 Chapter Contents

d06 Chapter Introduction

NAG Library Manual