s20ac:: Approximations of Special Functions (NAG Toolbox)

nag_specfun_fresnel_s (s20ac) evaluates an approximation to the Fresnel integral

S (x) = \int_{0}^{x} \sin (\frac{π}{2} t^{2}) d t .

Note:

S (x) = - S (- x)

, so the approximation need only consider

x \geq 0.0

The function is based on three Chebyshev expansions:

For

0 < x \leq 3

S (x) = x^{3} \underset{r = 0}{\sum^{'}} a_{r} T_{r} (t),   with ​ t = 2 {(\frac{x}{3})}^{4} - 1 .

For

x > 3

S (x) = \frac{1}{2} - \frac{f (x)}{x} \cos (\frac{π}{2} x^{2}) - \frac{g (x)}{x^{3}} \sin (\frac{π}{2} x^{2}),

where

f (x) = \underset{r = 0}{\sum^{'}} b_{r} T_{r} (t)

and

g (x) = \underset{r = 0}{\sum^{'}} c_{r} T_{r} (t)

with

t = 2 {(\frac{3}{x})}^{4} - 1

For small

x

S (x) ≃ \frac{π}{6} x^{3}

. This approximation is used when

x

is sufficiently small for the result to be correct to machine precision. For very small

x

, this approximation would underflow; the result is then set exactly to zero.

For large

x

f (x) ≃ \frac{1}{π}

and

g (x) ≃ \frac{1}{π^{2}}

. Therefore for moderately large

x

, when

\frac{1}{π^{2} x^{3}}

is negligible compared with

\frac{1}{2}

, the second term in the approximation for

x > 3

may be dropped. For very large

x

, when

\frac{1}{π x}

becomes negligible,

S (x) ≃ \frac{1}{2}

. However there will be considerable difficulties in calculating

\cos (\frac{π}{2} x^{2})

accurately before this final limiting value can be used. Since

\cos (\frac{π}{2} x^{2})

is periodic, its value is essentially determined by the fractional part of

x^{2}

. If

x^{2} = N + θ

where

N

is an integer and

0 \leq θ < 1

, then

\cos (\frac{π}{2} x^{2})

depends on

θ

and on

N

modulo

4

. By exploiting this fact, it is possible to retain significance in the calculation of

\cos (\frac{π}{2} x^{2})

either all the way to the very large

x

limit, or at least until the integer part of

\frac{x}{2}

is equal to the maximum integer allowed on the machine.

References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Parameters

Compulsory Input Parameters

Optional Input Parameters

Output Parameters

Error Indicators and Warnings

There are no failure exits from nag_specfun_fresnel_s (s20ac). The argument ifail has been included for consistency with other functions in this chapter.

Accuracy

Let

δ

and

ε

be the relative errors in the argument and result respectively.

δ

is somewhat larger than the machine precision (i.e., if

δ

is due to data errors etc.), then

ε

and

δ

are approximately related by:

ε ≃ |\frac{x \sin (\frac{π}{2} x^{2})}{S (x)}| δ .

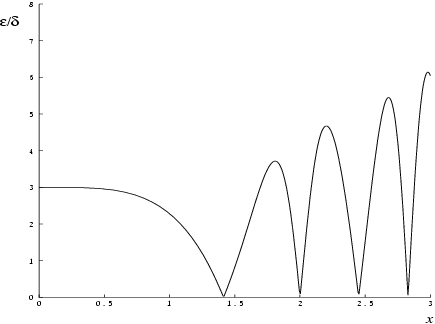
Figure 1 shows the behaviour of the error amplification factor

|\frac{x \sin (\frac{π}{2} x^{2})}{S (x)}|

However if

δ

is of the same order as the machine precision, then rounding errors could make

ε

slightly larger than the above relation predicts.

For small

x

ε ≃ 3 δ

and hence there is only moderate amplification of relative error. Of course for very small

x

where the correct result would underflow and exact zero is returned, relative error-control is lost.

For moderately large values of

x

|ε| ≃ |2 x \sin (\frac{π}{2} x^{2})| |δ|

and the result will be subject to increasingly large amplification of errors. However the above relation breaks down for large values of

x

(i.e., when

\frac{1}{x^{2}}

is of the order of the machine precision); in this region the relative error in the result is essentially bounded by

\frac{2}{π x}

Hence the effects of error amplification are limited and at worst the relative error loss should not exceed half the possible number of significant figures.

Further Comments

Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

function s20ac_example


fprintf('s20ac example results\n\n');

x = [0   0.5   1   2   4   5   6   8   10   -1   1000];
n = size(x,2);
result = x;

for j=1:n
  [result(j), ifail] = s20ac(x(j));
end

disp('      x          S(x)');
fprintf('%12.3e%12.3e\n',[x; result]);

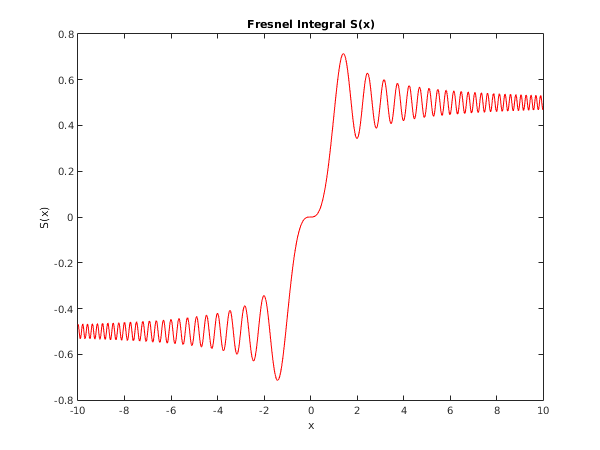
s20ac_plot;



function s20ac_plot
  x = [-10:0.02:10];
  for j = 1:numel(x)
    [S(j), ifail] = s20ac(x(j));
  end

  fig1 = figure;
  plot(x,S,'-r');
  xlabel('x');
  ylabel('S(x)');
  title('Fresnel Integral S(x)');

s20ac example results

      x          S(x)
   0.000e+00   0.000e+00
   5.000e-01   6.473e-02
   1.000e+00   4.383e-01
   2.000e+00   3.434e-01
   4.000e+00   4.205e-01
   5.000e+00   4.992e-01
   6.000e+00   4.470e-01
   8.000e+00   4.602e-01
   1.000e+01   4.682e-01
  -1.000e+00  -4.383e-01
   1.000e+03   4.997e-01

NAG Toolbox: nag_specfun_fresnel_s (s20ac)

▸▿ Contents

Purpose

Syntax

Description