, it becomes impossible to provide results with any reasonable accuracy (see Accuracy), hence the function fails. Such arguments contain insufficient information to determine the phase of oscillation of

J_{0} (x)

; only the amplitude,

\sqrt{\frac{2}{π |x|}}

, can be determined and this is returned on soft failure. The range for which this occurs is roughly related to machine precision; the function will fail if

|x| ≳ 1 / machine precision

References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Clenshaw C W (1962) Chebyshev Series for Mathematical Functions Mathematical tables HMSO

Parameters

Compulsory Input Parameters

1: $x$ – double scalar: The argument $x$ of the function.

Optional Input Parameters

None.

Output Parameters

1: $result$ – double scalar: The result of the function.
2: $ifail$ – int64int32nag_int scalar: $ifail = 0$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:

$ifail = 1$: x is too large. On soft failure the function returns the amplitude of the $J_{0}$ oscillation, $\sqrt{\frac{2}{π |x|}}$ .

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.

$ifail = - 999$: Dynamic memory allocation failed.

Accuracy

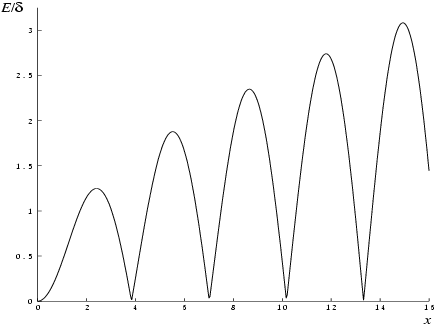
Let

δ

be the relative error in the argument and

E

be the absolute error in the result. (Since

J_{0} (x)

oscillates about zero, absolute error and not relative error is significant.)

δ

is somewhat larger than the machine precision (e.g., if

δ

is due to data errors etc.), then

E

and

δ

are approximately related by:

E ≃ |x J_{1} (x)| δ

(provided

E

is also within machine bounds). Figure 1 displays the behaviour of the amplification factor

|x J_{1} (x)|

However, if

δ

is of the same order as machine precision, then rounding errors could make

E

slightly larger than the above relation predicts.

For very large

x

, the above relation ceases to apply. In this region,

J_{0} (x) ≃ \sqrt{\frac{2}{π |x|}} \cos (x - \frac{π}{4})

. The amplitude

\sqrt{\frac{2}{π |x|}}

can be calculated with reasonable accuracy for all

x

, but

\cos (x - \frac{π}{4})

cannot. If

x - \frac{π}{4}

is written as

2 N π + θ

where

N

is an integer and

0 \leq θ < 2 π

, then

\cos (x - \frac{π}{4})

is determined by

θ

only. If

x ≳ δ^{- 1}

θ

cannot be determined with any accuracy at all. Thus if

x

is greater than, or of the order of, the inverse of the machine precision, it is impossible to calculate the phase of

J_{0} (x)

and the function must fail.

Figure 1

Further Comments

None.

Example

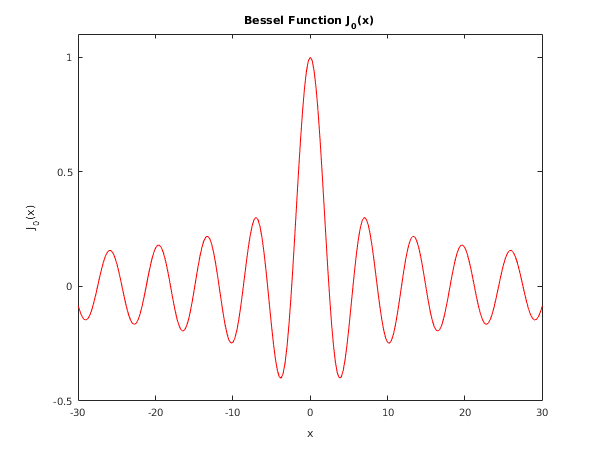
This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

Open in the MATLAB editor: s17ae_example

function s17ae_example


fprintf('s17ae example results\n\n');

x = [0    0.5     1    3    6   8    10   -1    1000];
n = size(x,2);
result = x;

for j=1:n
  [result(j), ifail] = s17ae(x(j));
end

disp('      x         J_0(x)');
fprintf('%12.3e%12.3e\n',[x; result]);

s17ae_plot;



function s17ae_plot
x = [-30:0.25:30];
  for j = 1:numel(x)
    [J0(j), ifail] = s17ae(x(j));
  end

  fig1 = figure;
  plot(x,J0,'-r');
  xlabel('x');
  ylabel('J_0(x)');
  title('Bessel Function J_0(x)');
  axis([-30 30 -0.5 1.1]);

s17ae example results

      x         J_0(x)
   0.000e+00   1.000e+00
   5.000e-01   9.385e-01
   1.000e+00   7.652e-01
   3.000e+00  -2.601e-01
   6.000e+00   1.506e-01
   8.000e+00   1.717e-01
   1.000e+01  -2.459e-01
  -1.000e+00   7.652e-01
   1.000e+03   2.479e-02

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox