is the maximum number of decimal digits that can be accurately represented for the particular implementation (see nag_machine_decimal_digits (x02be)).

For

|x| \geq x_{hi}

there is a danger of setting underflow in

erfc (x)

. For

x \geq x_{hi}

, nag_specfun_erfc_real (s15ad) returns

erfc (x) = 0

; for

x \leq - x_{hi}

it returns

erfc (x) = 2

References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Cody W J (1969) Rational Chebyshev approximations for the error function Math.Comp. 23 631–637

Parameters

Compulsory Input Parameters

1: $x$ – double scalar: The argument $x$ of the function.

Optional Input Parameters

None.

Output Parameters

1: $result$ – double scalar: The result of the function.
2: $ifail$ – int64int32nag_int scalar: $ifail = 0$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

There are no failure exits from nag_specfun_erfc_real (s15ad). The argument ifail has been included for consistency with other functions in this chapter.

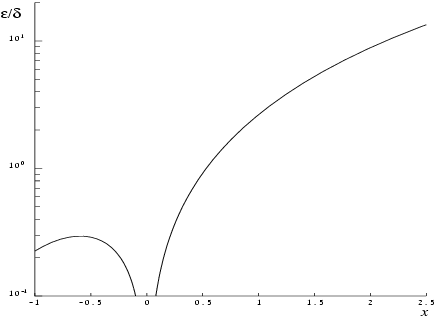
Accuracy

δ

and

ε

are relative errors in the argument and result, respectively, then in principle

|ε| ≃ |\frac{2 x e^{- x^{2}}}{\sqrt{π} erfc (x)} δ| .

That is, the relative error in the argument,

x

, is amplified by a factor

\frac{2 x e^{- x^{2}}}{\sqrt{π} erfc (x)}

in the result.

The behaviour of this factor is shown in Figure 1.

Figure 1

It should be noted that near

x = 0

this factor behaves as

\frac{2 x}{\sqrt{π}}

and hence the accuracy is largely determined by the machine precision. Also for large negative

x

, where the factor is

\sim \frac{x e^{- x^{2}}}{\sqrt{π}}

, accuracy is mainly limited by machine precision. However, for large positive

x

, the factor becomes

\sim 2 x^{2}

and to an extent relative accuracy is necessarily lost. The absolute accuracy

E

is given by

E ≃ \frac{2 x e^{- x^{2}}}{\sqrt{π}} δ

so absolute accuracy is guaranteed for all

x

Further Comments

None.

Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

Open in the MATLAB editor: s15ad_example

function s15ad_example


fprintf('s15ad example results\n\n');

x = [-10   -1     0    1     10];
n = size(x,2);
result = x;

for j=1:n
  [result(j), ifail] = s15ad(x(j));
end

disp('      x         erfc(x)');
fprintf('%12.3e%12.3e\n',[x; result]);

s15ad example results

      x         erfc(x)
  -1.000e+01   2.000e+00
  -1.000e+00   1.843e+00
   0.000e+00   1.000e+00
   1.000e+00   1.573e-01
   1.000e+01   2.088e-45

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox