PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_specfun_gamma_incomplete (s14ba)
Purpose
nag_specfun_gamma_incomplete (s14ba) computes values for the incomplete gamma functions and .
Syntax
Description
nag_specfun_gamma_incomplete (s14ba) evaluates the incomplete gamma functions in the normalized form
with
and
, to a user-specified accuracy. With this normalization,
.
Several methods are used to evaluate the functions depending on the arguments
and
, the methods including Taylor expansion for
, Legendre's continued fraction for
, and power series for
. When both
and
are large, and
, the uniform asymptotic expansion of
Temme (1987) is employed for greater efficiency – specifically, this expansion is used when
and
.
Once either or is computed, the other is obtained by subtraction from . In order to avoid loss of relative precision in this subtraction, the smaller of and is computed first.
This function is derived from the function GAM in
Gautschi (1979b).
References
Gautschi W (1979a) A computational procedure for incomplete gamma functions ACM Trans. Math. Software 5 466–481
Gautschi W (1979b) Algorithm 542: Incomplete gamma functions ACM Trans. Math. Software 5 482–489
Temme N M (1987) On the computation of the incomplete gamma functions for large values of the parameters Algorithms for Approximation (eds J C Mason and M G Cox) Oxford University Press
Parameters
Compulsory Input Parameters
- 1:
– double scalar
-
The argument of the functions.
Constraint:
.
- 2:
– double scalar
-
The argument of the functions.
Constraint:
.
- 3:
– double scalar
-
The relative accuracy required by you in the results. If
nag_specfun_gamma_incomplete (s14ba) is entered with
tol greater than
or less than
machine precision, then the value of
machine precision is used instead.
Optional Input Parameters
None.
Output Parameters
- 1:
– double scalar
- 2:
– double scalar
-
The values of the functions and respectively.
- 3:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
-
-
-
-
Convergence of the Taylor series or Legendre continued fraction fails within
iterations. This error is extremely unlikely to occur; if it does, contact
NAG.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
There are rare occasions when the relative accuracy attained is somewhat less than that specified by argument
tol. However, the error should never exceed more than one or two decimal places. Note also that there is a limit of
decimal places on the achievable accuracy, because constants in the function are given to this precision.
Further Comments
The time taken for a call of
nag_specfun_gamma_incomplete (s14ba) depends on the precision requested through
tol, and also varies slightly with the input arguments
and
.
Example
This example reads values of the argument and from a file, evaluates the function and prints the results.
Open in the MATLAB editor:
s14ba_example
function s14ba_example
fprintf('s14ba example results\n\n');
a = [ 2 7 0.5 20 21];
x = [ 3 1 99.0 21 20];
n = size(x,2);
p = x;
q = x;
tol = x02aj;
for j=1:n
[p(j), q(j), ifail] = s14ba(a(j), x(j), tol);
end
disp(' a x P(a,x) Q(a,x)');
fprintf('%7.1f%7.1f%10.4f%10.4f\n',[a; x; p; q]);
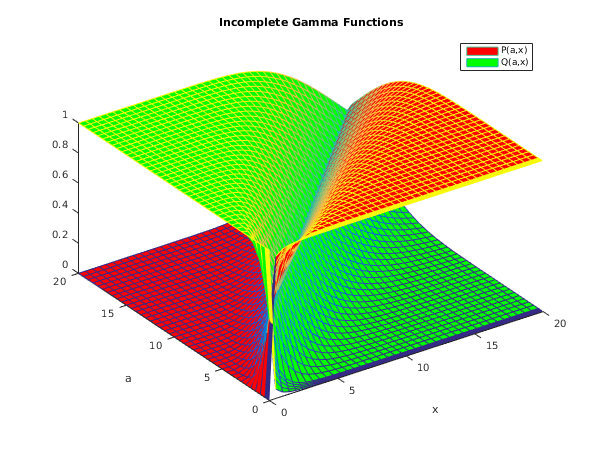
s14ba_plot;
function s14ba_plot
x = [0:0.5:20];
a = [0.1:0.1:0.4,0.5:0.5:20];
p = zeros(numel(a),numel(x));
q = p;
tol = x02aj;
for i=1:numel(a)
for j=1:numel(x)
[p(i,j), q(i,j), ifail] = s14ba(a(i), x(j), tol);
end
end
fig1 = figure;
hold on
mesh(x, a, p, 'FaceColor','r');
mesh(x, a, q, 'FaceColor','g');
xlabel('x');
ylabel('a');
title('Incomplete Gamma Functions');
legend('P(a,x)','Q(a,x)');
view(-35, 46);
hold off;
s14ba example results
a x P(a,x) Q(a,x)
2.0 3.0 0.8009 0.1991
7.0 1.0 0.0001 0.9999
0.5 99.0 1.0000 0.0000
20.0 21.0 0.6157 0.3843
21.0 20.0 0.4409 0.5591
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015