PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_specfun_sinh (s10ab)
Purpose
nag_specfun_sinh (s10ab) returns the value of the hyperbolic sine, , via the function name.
Syntax
Description
nag_specfun_sinh (s10ab) calculates an approximate value for the hyperbolic sine of its argument,
.
For
it uses the Chebyshev expansion
where
.
For
where is a machine-dependent constant.
For , the function fails owing to the danger of setting overflow in calculating . The result returned for such calls is , i.e., it returns the result for the nearest valid argument.
References
Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications
Parameters
Compulsory Input Parameters
- 1:
– double scalar
-
The argument of the function.
Optional Input Parameters
None.
Output Parameters
- 1:
– double scalar
The result of the function.
- 2:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
- W
-
The function has been called with an argument too large in absolute magnitude. There is a danger of setting overflow. The result is the value of at the closest argument for which a valid call could be made.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
If
and
are the relative errors in the argument and result, respectively, then in principle
That is the relative error in the argument,
, is amplified by a factor, approximately
. The equality should hold if
is greater than the
machine precision (
is a result of data errors etc.) but, if
is simply a result of round-off in the machine representation of
, then it is possible that an extra figure may be lost in internal calculation round-off.
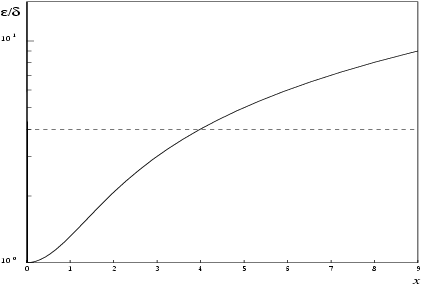
The behaviour of the error amplification factor can be seen in the following graph:
Figure 1
It should be noted that for
where
is the absolute error in the argument.
Further Comments
None.
Example
This example reads values of the argument from a file, evaluates the function at each value of and prints the results.
Open in the MATLAB editor:
s10ab_example
function s10ab_example
fprintf('s10ab example results\n\n');
x = [-10 -0.5 0 0.5 25];
n = size(x,2);
result = x;
for j=1:n
[result(j), ifail] = s10ab(x(j));
end
disp(' x sinh(x)');
fprintf('%12.3e%12.3e\n',[x; result]);
s10ab example results
x sinh(x)
-1.000e+01 -1.101e+04
-5.000e-01 -5.211e-01
0.000e+00 0.000e+00
5.000e-01 5.211e-01
2.500e+01 3.600e+10
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015