1: $result$ – double scalar: The result of the function.
2: $ifail$ – int64int32nag_int scalar: $ifail = 0$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

None.

Accuracy

δ

and

ε

are the relative errors in the argument and the result respectively, then in principle,

|ε| ≃ |\frac{2 x}{\sinh 2 x} δ| .

That is, a relative error in the argument,

x

, is amplified by a factor approximately

\frac{2 x}{\sinh 2 x}

, in the result.

The equality should hold if

δ

is greater than the machine precision (

δ

due to data errors etc.) but if

δ

is due simply to the round-off in the machine representation it is possible that an extra figure may be lost in internal calculation round-off.

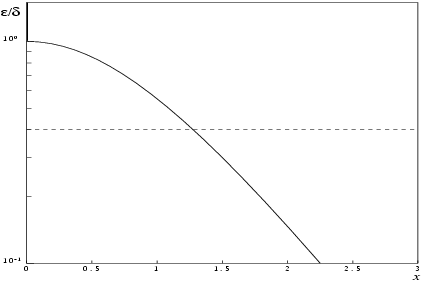
The behaviour of the amplification factor is shown in the following graph:

Figure 1

It should be noted that this factor is always less than or equal to

1.0

and away from

x = 0

the accuracy will eventually be limited entirely by the precision of machine representation.

Further Comments

None.

Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

Open in the MATLAB editor: s10aa_example

function s10aa_example


fprintf('s10aa example results\n\n');

x = [20.0  -5.0    0.5     5.0];
n = size(x,2);
result = x;

for j=1:n
  [result(j), ifail] = s10aa(x(j));
end

disp('      x         tanh(x)');
fprintf('%12.3e%12.3e\n',[x; result]);

s10aa example results

      x         tanh(x)
   2.000e+01   1.000e+00
  -5.000e+00  -9.999e-01
   5.000e-01   4.621e-01
   5.000e+00   9.999e-01

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox