PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_specfun_arcsin (s09aa)
Purpose
nag_specfun_arcsin (s09aa) returns the value of the inverse circular sine, , via the function name. The value is in the principal range .
Syntax
Description
nag_specfun_arcsin (s09aa) calculates an approximate value for the inverse circular sine,
. It is based on the Chebyshev expansion
where
and
.
For .
For .
For is undefined and the function fails.
References
Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications
Parameters
Compulsory Input Parameters
- 1:
– double scalar
-
The argument of the function.
Constraint:
.
Optional Input Parameters
None.
Output Parameters
- 1:
– double scalar
The result of the function.
- 2:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
The function has been called with an argument greater than in absolute value; is undefined and the function returns zero.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
If
and
are the relative errors in the argument and result, respectively, then in principle
That is, a relative error in the argument
is amplified by at least a factor
in the result.
The equality should hold if
is greater than the
machine precision (
is a result of data errors etc.) but if
is produced simply by round-off error in the machine it is possible that rounding in internal calculations may lose an extra figure in the result.
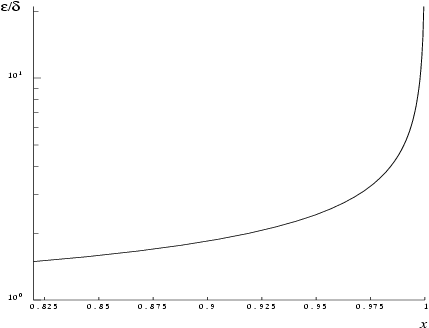
This factor stays close to one except near where its behaviour is shown in the following graph.
For close to unity, , the above analysis is no longer applicable owing to the fact that both argument and result are subject to finite bounds, ( and ). In this region ; that is the result will have approximately half as many correct significant figures as the argument.
For
the result will be correct to full
machine precision.
Further Comments
None.
Example
This example reads values of the argument from a file, evaluates the function at each value of and prints the results.
Open in the MATLAB editor:
s09aa_example
function s09aa_example
fprintf('s09aa example results\n\n');
x = [ -0.5 0.1 0.9];
n = size(x,2);
result = x;
for j=1:n
[result(j), ifail] = s09aa(x(j));
end
disp(' x arcsin(x)');
fprintf('%12.3e%12.3e\n',[x; result]);
s09aa example results
x arcsin(x)
-5.000e-01 -5.236e-01
1.000e-01 1.002e-01
9.000e-01 1.120e+00
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015