PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_mv_cluster_hier_dendrogram (g03eh)
Purpose
nag_mv_cluster_hier_dendrogram (g03eh) produces a dendrogram from the results of
nag_mv_cluster_hier (g03ec).
Syntax
Description
Hierarchical cluster analysis, as performed by
nag_mv_cluster_hier (g03ec), can be represented by a tree that shows at which distance the clusters merge. Such a tree is known as a dendrogram. See
Everitt (1974) and
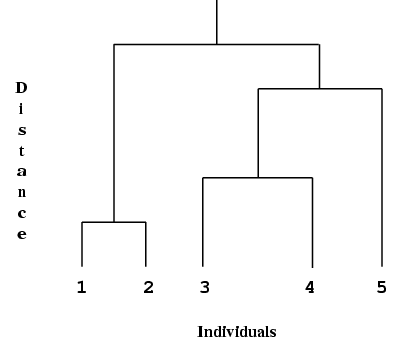
Krzanowski (1990) for examples of dendrograms. A simple example is,
The end points of the dendrogram represent the objects that have been clustered. They should be in a suitable order as given by
nag_mv_cluster_hier (g03ec). Object
is always the first object. In the example above the height represents the distance at which the clusters merge.
The dendrogram is produced in
a character array
using the ordering and distances provided by
nag_mv_cluster_hier (g03ec). Suitable characters are used to represent parts of the tree.
There are four possible orientations for the dendrogram. The example above has the end points at the bottom of the diagram which will be referred to as south. If the dendrogram was the other way around with the end points at the top of the diagram then the orientation would be north. If the end points are at the left-hand or right-hand side of the diagram the orientation is west or east. Different symbols are used for east/west and north/south orientations.
References
Everitt B S (1974) Cluster Analysis Heinemann
Krzanowski W J (1990) Principles of Multivariate Analysis Oxford University Press
Parameters
Compulsory Input Parameters
- 1:
– string (length ≥ 1)
-
Indicates which orientation the dendrogram is to take.
- The end points of the dendrogram are to the north.
- The end points of the dendrogram are to the south.
- The end points of the dendrogram are to the east.
- The end points of the dendrogram are to the west.
Constraint:
, , or .
- 2:
– double array
-
The array
dord as output by
nag_mv_cluster_hier (g03ec).
dord contains the distances, in dendrogram order, at which clustering takes place.
Constraint:
, for .
- 3:
– double scalar
-
The clustering distance at which the dendrogram begins.
Constraint:
.
- 4:
– double scalar
-
The distance represented by one symbol of the dendrogram.
Constraint:
.
- 5:
– int64int32nag_int scalar
-
The number of character positions used in the dendrogram. Hence the clustering distance at which the dendrogram terminates is given by .
Constraint:
.
- 6:
– int64int32nag_int scalar
-
The dimension of the array
c.
Constraints:
- if or , ;
- if or , .
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the array
dord.
The number of objects in the cluster analysis.
Constraint:
.
Output Parameters
- 1:
– cell array of strings
-
The elements of
c contain consecutive lines of the dendrogram.
- 2:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
| On entry, | , |
| or | , |
| or | , |
| or | , |
| or | , or 'W', |
| or | or , , |
| or | or , , |
| or | the number of characters that can be stored in each element of array c is insufficient for the requested orientation. |
-
-
| On entry, | , for some . |
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
Not applicable.
Further Comments
The scale of the dendrogram is controlled by
dstep. The smaller the value
dstep is, the greater the amount of detail that will be given but
nsym will have to be larger to give the full dendrogram. The range of distances represented by the dendrogram is
dmin to
. The values of
dmin,
dstep and
nsym can thus be set so that only part of the dendrogram is produced.
The dendrogram does not include any labelling of the objects. You can print suitable labels using the ordering given by the array
iord returned by
nag_mv_cluster_hier (g03ec).
Example
Data consisting of three variables on five objects are read in. Euclidean squared distances are computed using
nag_mv_distance_mat (g03ea) and median clustering performed by
nag_mv_cluster_hier (g03ec).
nag_mv_cluster_hier_dendrogram (g03eh) is used to produce a dendrogram with orientation east and a dendrogram with orientation south. The two dendrograms are printed.
Open in the MATLAB editor:
g03eh_example
function g03eh_example
fprintf('g03eh example results\n\n');
x = [1, 1, 1;
2, 1, 2;
3, 6, 3;
4, 8, 2;
5, 8, 0];
[n,m] = size(x);
isx = ones(m,1,'int64');
isx(1) = int64(0);
s = ones(m,1);
ld = (n*(n-1))/2;
d = zeros(ld,1);
update = 'I';
dist = 'S';
scal = 'U';
[s, d, ifail] = g03ea( ...
update, dist, scal, x, isx, s, d);
method = int64(5);
n = int64(n);
[d, ilc, iuc, cd, iord, dord, ifail] = ...
g03ec(method, n, d);
orient = 'East';
fprintf('Dendrogram, Orientation %s\n', orient);
dmin = 0;
dstep = 1.1;
nsym = int64(40);
lenc = int64(n);
[c, ifail] = g03eh( ...
orient, dord, dmin, dstep, nsym, lenc);
for i = 1:lenc
fprintf('%s\n',c{i});
end
orient = 'South';
fprintf('\nDendrogram, Orientation %s\n', orient);
dstep = 1.0;
lenc = int64(nsym);
[c, ifail] = g03eh( ...
orient, dord, dmin, dstep, nsym, lenc);
for i = 1:lenc
fprintf('%s\n',c{i});
end
g03eh example results
Dendrogram, Orientation East
...............................(
( .......
( ( ...
(........................(...(...
Dendrogram, Orientation South
----------
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I I
I ------*
I I I
I I I
I I I
I I ---*
I I I I
I I I I
---* I I I
I I I I I
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015