PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_glopt_bnd_mcs_solve (e05jb)
Purpose
nag_glopt_bnd_mcs_solve (e05jb) is designed to find the global minimum or maximum of an arbitrary function, subject to simple bound-constraints using a multi-level coordinate search method. Derivatives are not required, but convergence is only guaranteed if the objective function is continuous in a neighbourhood of a global optimum. It is not intended for large problems.
The initialization function
nag_glopt_bnd_mcs_init (e05ja) must have been called before calling
nag_glopt_bnd_mcs_solve (e05jb).
Syntax
[
bl,
bu,
list,
numpts,
initpt,
x,
obj,
comm,
user,
ifail] = e05jb(
objfun,
ibound,
bl,
bu,
list,
numpts,
initpt,
monit,
comm, 'n',
n, 'iinit',
iinit, 'sdlist',
sdlist, 'user',
user)
[
bl,
bu,
list,
numpts,
initpt,
x,
obj,
comm,
user,
ifail] = nag_glopt_bnd_mcs_solve(
objfun,
ibound,
bl,
bu,
list,
numpts,
initpt,
monit,
comm, 'n',
n, 'iinit',
iinit, 'sdlist',
sdlist, 'user',
user)
Note: the interface to this routine has changed since earlier releases of the toolbox:
| At Mark 24: |
iinit was made optional |
Description
nag_glopt_bnd_mcs_solve (e05jb) is designed to solve modestly sized global optimization problems having simple bound-constraints only; it finds the global optimum of a nonlinear function subject to a set of bound constraints on the variables. Without loss of generality, the problem is assumed to be stated in the following form:
where
(the
objective function) is a nonlinear scalar function (assumed to be continuous in a neighbourhood of a global minimum), and the bound vectors are elements of
, where
denotes the extended reals
. Relational operators between vectors are interpreted elementwise.
The optional parameter
Maximize should be set if you wish to solve maximization, rather than minimization, problems.
If certain bounds are not present, the associated elements of
or
can be set to special values that will be treated as
or
. See the description of the optional parameter
Infinite Bound Size. Phrases in this document containing terms like ‘unbounded values’ should be understood to be taken relative to this optional parameter.
Fixing variables (that is, setting for some ) is allowed in nag_glopt_bnd_mcs_solve (e05jb).
A typical excerpt from a function calling
nag_glopt_bnd_mcs_solve (e05jb) is:
[comm, ifail] = e05ja(n_r);
[comm, ifail] = e05jd(optstr, comm);
[..., ifail] = e05jb(objfun, ...);
where
nag_glopt_bnd_mcs_optset_string (e05jd) sets the optional parameter and value specified in
optstr.
The initialization function
nag_glopt_bnd_mcs_init (e05ja) does not need to be called before each invocation of
nag_glopt_bnd_mcs_solve (e05jb). You should be aware that a call to the initialization function will reset each optional parameter to its default value, and, if you are using repeatable randomized initialization lists (see the description of the argument
iinit), the random state stored in
the array
comm
will be destroyed.
You must supply a function that evaluates ; derivatives are not required.
The method used by
nag_glopt_bnd_mcs_solve (e05jb) is based on MCS, the Multi-level Coordinate Search method described in
Huyer and Neumaier (1999), and the algorithm it uses is described in detail in
Algorithmic Details.
References
Huyer W and Neumaier A (1999) Global optimization by multi-level coordinate search Journal of Global Optimization 14 331–355
Parameters
Compulsory Input Parameters
- 1:
– function handle or string containing name of m-file
-
objfun must evaluate the objective function
for a specified
-vector
.
[f, user, inform] = objfun(n, x, nstate, user)
Input Parameters
- 1:
– int64int32nag_int scalar
-
, the number of variables.
- 2:
– double array
-
, the vector at which the objective function is to be evaluated.
- 3:
– int64int32nag_int scalar
-
If
then
nag_glopt_bnd_mcs_solve (e05jb) is calling
objfun for the first time. This argument setting allows you to save computation time if certain data must be read or calculated only once.
- 4:
– Any MATLAB object
objfun is called from
nag_glopt_bnd_mcs_solve (e05jb) with the object supplied to
nag_glopt_bnd_mcs_solve (e05jb).
Output Parameters
- 1:
– double scalar
-
Must be set to the value of the objective function at
, unless you have specified termination of the current problem using
inform.
- 2:
– Any MATLAB object
- 3:
– int64int32nag_int scalar
-
Must be set to a value describing the action to be taken by the solver on return from
objfun. Specifically, if the value is negative the solution of the current problem will terminate immediately; otherwise, computations will continue.
- 2:
– int64int32nag_int scalar
-
Indicates whether the facility for dealing with bounds of special forms is to be used.
ibound must be set to one of the following values.
- You will supply and individually.
- There are no bounds on .
- There are semi-infinite bounds .
- There are constant bounds and .
Note that it only makes sense to fix any components of when .
Constraint:
, , or .
- 3:
– double array
- 4:
– double array
-
is
, the array of lower bounds.
is
, the array of upper bounds.
If
, you must set
to
and
to
, for
. If a particular
is to be unbounded below, the corresponding
should be set to
, where
is the value of the optional parameter
Infinite Bound Size. Similarly, if a particular
is to be unbounded above, the corresponding
should be set to
.
If
or
, arrays
bl and
bu need not be set on input.
If
, you must set
to
and
to
. The remaining elements of
bl and
bu will then be populated by these initial values.
Constraints:
- if , , for ;
- if , .
- 5:
– double array
-
This argument need not be set on entry if you wish to use one of the preset initialization methods (
).
list is the ‘initialization list’: whenever a sub-box in the algorithm is split for the first time (either during the
initialization procedure or later), for each non-fixed coordinate
the split is done at the values
, as well as at some adaptively chosen intermediate points. The array sections
, for
, must be in ascending order with each entry being distinct. In this context, ‘distinct’ should be taken to mean relative to the safe-range argument (see
nag_machine_real_safe (x02am)).
Constraint:
if is not fixed, is in ascending order with each entry being distinct, for , for and .
- 6:
– int64int32nag_int array
-
This argument need not be set on entry if you wish to use one of the preset initialization methods (
).
numpts encodes the number of splitting points in each non-fixed dimension.
Constraints:
- if is not fixed, ;
- , for .
- 7:
– int64int32nag_int array
-
This argument need not be set on entry if you wish to use one of the preset initialization methods (
).
You must designate a point stored in
list that you wish
nag_glopt_bnd_mcs_solve (e05jb) to consider as an ‘initial point’ for the purposes of the splitting procedure. Call this initial point
. The coordinates of
correspond to a set of indices
, for
, such that
is stored in
, for
. You must set
, for
.
Constraint:
if is not fixed, , for .
- 8:
– function handle or string containing name of m-file
-
monit may be used to monitor the optimization process. It is invoked upon every successful completion of the procedure in which a sub-box is considered for splitting. It will also be called just before
nag_glopt_bnd_mcs_solve (e05jb) exits if that splitting procedure was not successful.
If no monitoring is required,
monit may be
string
nag_glopt_bnd_mcs_dummy_monit (e05jbk)
[user, inform] = monit(n, ncall, xbest, icount, ninit, list, numpts, initpt, nbaskt, xbaskt, boxl, boxu, nstate, user)
Input Parameters
- 1:
– int64int32nag_int scalar
-
, the number of variables.
- 2:
– int64int32nag_int scalar
-
The cumulative number of calls to
objfun.
- 3:
– double array
-
The current best point.
- 4:
– int64int32nag_int array
-
An array of counters.
- , the current number of sub-boxes.
- , the cumulative number of calls to objfun made in local searches.
- , the cumulative number of points used as start points for local searches.
- , the cumulative number of sweeps through levels.
- , the cumulative number of splits by initialization list.
- , the current lowest level containing non-split boxes.
- 5:
– int64int32nag_int scalar
-
The maximum over
of the number of points in coordinate
at which to split according to the initialization list
list. See also the description of the argument
numpts.
- 6:
– double array
-
The initialization list.
- 7:
– int64int32nag_int array
-
The number of points in each coordinate at which to split according to the initialization list
list.
- 8:
– int64int32nag_int array
-
A pointer to the ‘initial point’ in
list. Element
is the column index in
list of the
th coordinate of the initial point.
- 9:
– int64int32nag_int scalar
-
The number of points in the ‘shopping basket’
xbaskt.
- 10:
– double array
-
Note: the th candidate minimum has its th coordinate stored in
, for and .
The ‘shopping basket’ of candidate minima.
- 11:
– double array
-
The array of lower bounds of the current search box.
- 12:
– double array
-
The array of upper bounds of the current search box.
- 13:
– int64int32nag_int scalar
-
Is set by
nag_glopt_bnd_mcs_solve (e05jb) to indicate at what stage of the minimization
monit was called.
- This is the first time that monit has been called.
- This is the last time monit will be called.
- This is the first and last time monit will be called.
- 14:
– Any MATLAB object
monit is called from
nag_glopt_bnd_mcs_solve (e05jb) with the object supplied to
nag_glopt_bnd_mcs_solve (e05jb).
Output Parameters
- 1:
– Any MATLAB object
- 2:
– int64int32nag_int scalar
-
Must be set to a value describing the action to be taken by the solver on return from
monit. Specifically, if the value is negative the solution of the current problem will terminate immediately; otherwise, computations will continue.
- 9:
– double array
-
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the arrays
bl,
bu,
numpts,
initpt and the first dimension of the array
list. (An error is raised if these dimensions are not equal.)
, the number of variables.
Constraint:
.
- 2:
– int64int32nag_int scalar
Default:
Selects which initialization method to use.
- Simple initialization (boundary and midpoint), with
, and
,
for and .
- Simple initialization (off-boundary and midpoint), with
, and
,
for and .
- Initialization using linesearches.
- You are providing your own initialization list.
- Generate a random initialization list.
For more information on methods
,
or
see
Initialization and Sweeps.
If ‘infinite’ values (as determined by the value of the optional parameter
Infinite Bound Size) are detected by
nag_glopt_bnd_mcs_solve (e05jb) when you are using a simple initialization method (
or
), a safeguarded initialization procedure will be attempted, to avoid overflow.
Constraint:
, , , or .
- 3:
– int64int32nag_int scalar
-
Default:
the second dimension of the array
list.
The second dimension of the array
list.
sdlist is, at least, the maximum over
of the number of points in coordinate
at which to split according to the initialization list
list; that is,
.
Internally,
nag_glopt_bnd_mcs_solve (e05jb) uses
list to determine sets of points along each coordinate direction to which it fits quadratic interpolants. Since fitting a quadratic requires at least three distinct points, this puts a lower bound on
sdlist. Furthermore, in the case of initialization by linesearches (
) internal storage considerations require that
sdlist be at least
, but not all of this space may be used.
Constraints:
- if , ;
- if , ;
- if , .
- 4:
– Any MATLAB object
user is not used by
nag_glopt_bnd_mcs_solve (e05jb), but is passed to
objfun and
monit. Note that for large objects it may be more efficient to use a global variable which is accessible from the m-files than to use
user.
Output Parameters
- 1:
– double array
- 2:
– double array
-
Unless
or
on exit,
bl and
bu are the actual arrays of bounds used by
nag_glopt_bnd_mcs_solve (e05jb).
- 3:
– double array
-
Unless
,
or
on exit, the actual initialization data used by
nag_glopt_bnd_mcs_solve (e05jb). If you wish to monitor the contents of
list you are advised to do so solely through
monit, not through the output value here.
- 4:
– int64int32nag_int array
-
Unless , or on exit, the actual initialization data used by nag_glopt_bnd_mcs_solve (e05jb).
- 5:
– int64int32nag_int array
-
Unless , or on exit, the actual initialization data used by nag_glopt_bnd_mcs_solve (e05jb).
- 6:
– double array
-
If
, contains an estimate of the global optimum (see also
Accuracy).
- 7:
– double scalar
-
If
, contains the function value at
x.
If you request early termination of
nag_glopt_bnd_mcs_solve (e05jb) using
inform in
objfun or the analogous
inform in
monit, there is no guarantee that the function value at
x equals
obj.
- 8:
– double array
-
.
- 9:
– Any MATLAB object
- 10:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
nag_glopt_bnd_mcs_solve (e05jb) returns with
if your termination criterion has been met: either a target value has been found to the required relative error (as determined by the values of the optional parameters
Target Objective Value,
Target Objective Error and
Target Objective Safeguard), or the best function value was static for the number of sweeps through levels given by the optional parameter
Static Limit. The latter criterion is the default.
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
Constraint: .
Initialization function
nag_glopt_bnd_mcs_init (e05ja) has not been called.
-
-
A value of
Splits Limit (
) smaller than
was set.
Constraint: , , or .
Constraint: if then , for ; if then .
Constraint: if then .
Constraint: if then .
Constraint: if then .
Constraint: if is not fixed then , for .
Constraint: if is not fixed then , for .
Constraint: if is not fixed then , for and .
Constraint: if is not fixed then , for and .
Constraint: if is not fixed then , for .
Constraint: if is not fixed then , for .
Constraint: , , , or .
Constraint: .
On entry, user-supplied section contained distinct elements, and .
On entry, user-supplied section was not in ascending order.
The number of non-fixed variables .
Constraint: .
-
-
A finite initialization list could not be computed internally. Consider reformulating the bounds on the problem, try providing your own initialization list, use the randomization option (
) or vary the value of
Infinite Bound Size.
The user-supplied initialization list contained infinite values, as determined by the optional parameter
Infinite Bound Size.
-
-
The division procedure completed but your target value could not be reached.
Despite every sub-box being processed
Splits Limit times, the target value you provided in
Target Objective Value could not be found to the tolerances given in
Target Objective Error and
Target Objective Safeguard. You could try reducing
Splits Limit or the objective tolerances.
-
-
The function evaluations limit was exceeded.
Approximately
Function Evaluations Limit function calls have been made without your chosen termination criterion being satisfied.
- W
-
User-supplied monitoring function requested termination.
User-supplied objective function requested termination.
-
-
An error occurred during initialization. It is likely that points from the initialization list are very close together. Try relaxing the bounds on the variables or use a different initialization method.
An error occurred during linesearching.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
If
on exit, then the vector returned in the array
x is an estimate of the solution
whose function value satisfies your termination criterion: the function value was static for
Static Limit sweeps through levels, or
where
is the value of the optional parameter
Target Objective Value,
is the value of the optional parameter
Target Objective Error, and
is the value of the optional parameter
Target Objective Safeguard.
Further Comments
For each invocation of
nag_glopt_bnd_mcs_solve (e05jb), local workspace arrays of fixed length are allocated internally. The total size of these arrays amounts to
integer elements, where
is the value of the optional parameter
Splits Limit and
is the number of non-fixed variables, and
double elements. In addition, if you are using randomized initialization lists (see the description of the argument
iinit), a further
integer elements are allocated internally.
In order to keep track of the regions of the search space that have been visited while looking for a global optimum,
nag_glopt_bnd_mcs_solve (e05jb) internally allocates arrays of increasing sizes depending on the difficulty of the problem. Two of the main factors that govern the amount allocated are the number of sub-boxes (call this quantity
) and the number of points in the ‘shopping basket’ (the argument
nbaskt on entry to
monit). Safe, pessimistic upper bounds on these two quantities are so large as to be impractical. In fact, the worst-case number of sub-boxes for even the most simple initialization list (when
on entry to
monit) grows like
. Thus
nag_glopt_bnd_mcs_solve (e05jb) does not attempt to estimate in advance the final values of
or
nbaskt for a given problem. There are a total of
integer arrays and
double arrays whose lengths depend on
, and there are a total of
integer arrays and
double arrays whose lengths depend on
nbaskt.
nag_glopt_bnd_mcs_solve (e05jb) makes a fixed initial guess that the maximum number of sub-boxes required will be
and that the maximum number of points in the ‘shopping basket’ will be
. If ever a greater amount of sub-boxes or more room in the ‘shopping basket’ is required,
nag_glopt_bnd_mcs_solve (e05jb) performs reallocation, usually doubling the size of the inadequately-sized arrays. Clearly this process requires periods where the original array and its extension exist in memory simultaneously, so that the data within can be copied, which compounds the complexity of
nag_glopt_bnd_mcs_solve (e05jb)'s memory usage. It is possible (although not likely) that if your problem is particularly difficult to solve, or of a large size (hundreds of variables), you may run out of memory.
One array that could be dynamically resized by
nag_glopt_bnd_mcs_solve (e05jb) is the ‘shopping basket’ (
xbaskt on entry to
monit). If the initial attempt to allocate
doubles for this array fails,
monit will not be called on exit from
nag_glopt_bnd_mcs_solve (e05jb).
nag_glopt_bnd_mcs_solve (e05jb) performs better if your problem is well-scaled. It is worth trying (by guesswork perhaps) to rescale the problem if necessary, as sensible scaling will reduce the difficulty of the optimization problem, so that nag_glopt_bnd_mcs_solve (e05jb) will take less computer time.
Example
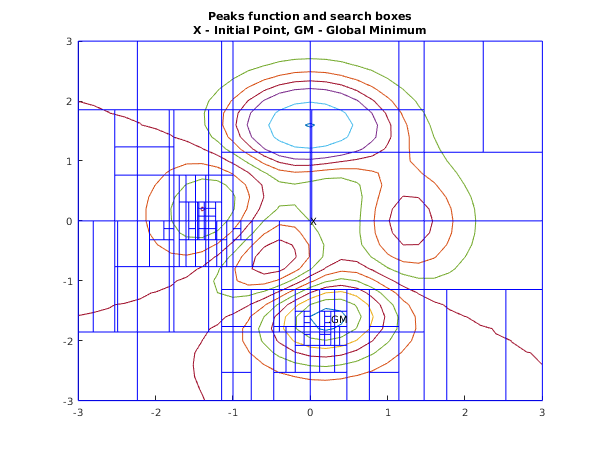
This example finds the global minimum of the ‘peaks’ function in two dimensions
on the box
.
The function has several local minima and one global minimum in the given box. The global minimum is approximately located at , where the function value is approximately .
We use default values for all the optional parameters, and we instruct nag_glopt_bnd_mcs_solve (e05jb) to use the simple initialization list corresponding to . In particular, this will set for us the initial point .
Open in the MATLAB editor:
e05jb_example
function e05jb_example
fprintf('e05jb example results\n\n');
prob = 'peaks';
xres = 100;
yres = 100;
n = 2;
bl = [-3; -3];
bu = -bl;
fglob = -6.55;
xglob = [0.23; -1.63];
fig1 = figure;
hold on
[xx,yy] = meshgrid([-3:0.2:3],[-3:0.2:3]);
z = peaks(xx,yy);exp(xx).*(4*xx.*(xx+yy)+2*yy.*(yy+1)+1);
[~,h] = contour(xx,yy,z);
h.LevelList = [-6:4,6,8];
colormap(lines);
[comm, ifail] = e05ja;
disp('Solve with no options or initial list data');
ibound = int64(0);
list = zeros(n,3);
numpts = zeros(n, 1, 'int64');
initpt = zeros(n, 1, 'int64');
[bl, bu, list, numpts, initpt, xbest, obj, comm, user, ifail] = ...
e05jb(...
@objective, ibound, bl, bu, list, numpts, initpt, @monitor, comm);
fprintf('xbest:\n ');
fprintf(' %7.3f',xbest);
fprintf('\nObjective Function:\n ');
fprintf(' %7.3f\n\n',obj);
fprintf('Solve with options and initial list data\n');
comm = e05jd('List', comm);
comm = e05jd('Function Evaluations Limit = 100000', comm);
comm = e05jf('Static Limit', int64(3*n), comm);
infbnd = e05jl('Infinite Bound Size', comm);
comm = e05jg('Infinite Bound Size', 10*infbnd, comm);
comm = e05je('Local Searches', 'on', comm);
iinit = int64(3);
list = zeros(n, 3);
list(:, 1) = bl;
list(:, 2) = [-1; 0];
list(:, 3) = bu;
numpts(1:n) = int64(3);
initpt(1:n) = int64(2);
[bl, bu, list, numpts, initpt, xbest, obj, comm, user, ifail] = ...
e05jb( ...
@objective, ibound, bl, bu, list, numpts, initpt, ...
@monitor, comm, 'iinit', iinit);
fprintf('xbest:\n ');
fprintf(' %7.3f',xbest);
fprintf('\nObjective Function:\n ');
fprintf(' %7.3f\n\n',obj);
text(0.23,-1.63,'.GM');
text(0,0,'X');
title({'Peaks function and search boxes', ...
'X - Initial Point, GM - Global Minimum'});
hold off
function [f,user,inform] = objective(n,x,nstate,user)
if (n==2)
inform = int64(0);
else
inform = int64(-1);
end
if (inform >= 0)
if (nstate == 1)
disp(sprintf('\n'));
disp('(OBJFUN was just called for the first time)');
end
f = peaks(x(1), x(2));
end
function [user,inform] = ...
monitor( ...
n,ncall,xbest,icount,ninit,list,numpts,initpt,nbaskt,...
xbaskt,boxl,boxu,nstate,user)
inform = int64(0);
if (nstate == 0 || nstate == 1)
fprintf('\n----- monitoring information ------\n');
end
if (nstate <= 0)
fprintf('Total sub-boxes = %5d\n', icount(1));
fprintf('Total function evaluations = %5d\n', ncall);
fprintf('Local function evaluations = %5d\n', icount(2));
fprintf('Points used in local search = %5d\n', icount(3));
fprintf('Total sweeps through levels = %5d\n', icount(4));
fprintf('Total splits by init. list = %5d\n', icount(5));
fprintf('Lowest unsplit level = %5d\n', icount(6));
fprintf('Candidate minima in basket = %5d\n', nbaskt);
fprintf('Shopping basket:\n');
fprintf(' %7.3f',xbaskt);
fprintf('\n');
fprintf('-----------------------------------\n');
else
plot([boxl(1) boxu(1) boxu(1) boxl(1) boxl(1)], ...
[boxl(2) boxl(2) boxu(2) boxu(2) boxl(2)], 'blue');
end
e05jb example results
Solve with no options or initial list data
(OBJFUN was just called for the first time)
----- monitoring information ------
Total sub-boxes = 228
Total function evaluations = 196
Local function evaluations = 87
Points used in local search = 13
Total sweeps through levels = 12
Total splits by init. list = 5
Lowest unsplit level = 7
Candidate minima in basket = 2
Shopping basket:
-1.347 0.205 0.228 -1.626
-----------------------------------
xbest:
0.228 -1.626
Objective Function:
-6.551
Solve with options and initial list data
FUNCTION EVALUATIONS LIMIT = 100000
STATIC LIMIT = 6
INFINITE BOUND SIZE = 1.1579208923731620E+78
LOCAL SEARCHES = on
(OBJFUN was just called for the first time)
----- monitoring information ------
Total sub-boxes = 146
Total function evaluations = 169
Local function evaluations = 102
Points used in local search = 7
Total sweeps through levels = 7
Total splits by init. list = 5
Lowest unsplit level = 4
Candidate minima in basket = 2
Shopping basket:
0.228 -1.626 -1.347 0.205
-----------------------------------
xbest:
0.228 -1.626
Objective Function:
-6.551
the remainder of this document is intended for more advanced users. Algorithmic Details contains a detailed description of the algorithm. This information may be needed in order to understand Optional Parameters, which describes the optional parameters that can be set by calls to nag_glopt_bnd_mcs_optset_string (e05jd), nag_glopt_bnd_mcs_optset_char (e05je), nag_glopt_bnd_mcs_optset_int (e05jf) and/or nag_glopt_bnd_mcs_optset_real (e05jg).
Algorithmic Details
Here we summarise the main features of the MCS algorithm used in
nag_glopt_bnd_mcs_solve (e05jb), and we introduce some terminology used in the description of the function and its arguments. We assume throughout that we will only do any work in coordinates
in which
is free to vary. The MCS algorithm is fully described in
Huyer and Neumaier (1999).
Initialization and Sweeps
Each sub-box is determined by a basepoint and an opposite point . We denote such a sub-box by . The basepoint is allowed to belong to more than one sub-box, is usually a boundary point, and is often a vertex.
An
initialization procedure produces an initial set of sub-boxes. Whenever a sub-box is split along a coordinate
for the first time (in the initialization procedure or later), the splitting is done at three or more user-defined values
at which the objective function is sampled, and at some adaptively chosen intermediate points. At least four children are generated. More precisely, we assume that we are given
and a vector
that, for each
, locates within
the
th coordinate of an
initial point ; that is, if
for some
, then
. A good guess for the global optimum can be used as
.
The initialization points and the vectors
and
are collectively called the
initialization list (and sometimes we will refer to just the initialization points as ‘the initialization list’, whenever this causes no confusion). The initialization data may be input by you, or they can be set to sensible default values by
nag_glopt_bnd_mcs_solve (e05jb): if you provide them yourself,
should contain
,
should contain
, and
should contain
, for
and
; if you wish
nag_glopt_bnd_mcs_solve (e05jb) to use one of its preset initialization methods, you could choose one of two simple, three-point methods (see
Figure 1). If the list generated by one of these methods contains infinite values, attempts are made to generate a safeguarded list using the function
(which is also used during the splitting procedure, and is described in
Splitting). If infinite values persist,
nag_glopt_bnd_mcs_solve (e05jb) exits with
. There is also the option to generate an initialization list with the aid of linesearches (by setting
). Starting with the absolutely smallest point in the root box, linesearches are made along each coordinate. For each coordinate, the local minimizers found by the linesearches are put into the initialization list. If there were fewer than three minimizers, they are augmented by close-by values. The final preset initialization option (
) generates a randomized list, so that independent multiple runs may be made if you suspect a global optimum has not been found. Each call to the initialization function
nag_glopt_bnd_mcs_init (e05ja) resets the initial-state vector for the Wichmann–Hill base-generator that is used. Depending on whether you set the optional parameter
Repeatability to
or
, the random state is initialized to give a repeatable or non-repeatable sequence. Then, a random integer between
and
sdlist is selected, which is then used to determine the number of points to be generated in each coordinate; that is,
numpts becomes a constant vector, set to this value. The components of
list are then generated, from a uniform distribution on the root box if the box is finite, or else in a safeguarded fashion if any bound is infinite. The array
is set to point to the best point in
list.
Given an initialization list (preset or otherwise),
nag_glopt_bnd_mcs_solve (e05jb) evaluates
at
, and sets the initial estimate of the global minimum,
, to
. Then, for
, the objective function
is evaluated at
points that agree with
in all but the
th coordinate. We obtain pairs
, for
, with:
, say; with, for
,
and with
The point having the smallest function value is renamed and the procedure is repeated with the next coordinate.
Once
nag_glopt_bnd_mcs_solve (e05jb) has a full set of initialization points and function values, it can generate an initial set of sub-boxes. Recall that the
root box is
, having basepoint
. The opposite point
is a corner of
farthest away from
, in some sense. The point
need not be a vertex of
, and
is entitled to have infinite coordinates. We loop over each coordinate
, splitting the current box along coordinate
into
,
or
sub-intervals with exactly one of the
as endpoints, depending on whether two, one or none of the
are on the boundary. Thus, as well as splitting at
, for
, we split at additional points
, for
. These additional
are such that
where
is the golden-section ratio
, and the exponent
takes the value
or
, chosen so that the sub-box with the smaller function value gets the larger fraction of the interval. Each child sub-box gets as basepoint the point obtained from
by changing
to the
that is a boundary point of the corresponding
th coordinate interval; this new basepoint therefore has function value
. The opposite point is derived from
by changing
to the other end of that interval.
nag_glopt_bnd_mcs_solve (e05jb) can now rank the coordinates based on an estimated variability of . For each we compute the union of the ranges of the quadratic interpolant through any three consecutive , taking the difference between the upper and lower bounds obtained as a measure of the variability of in coordinate . A vector is populated in such a way that coordinate has the th highest estimated variability. For tiebreaks, when the obtained after splitting coordinate belongs to two sub-boxes, the one that contains the minimizer of the quadratic models is designated the current sub-box for coordinate .
Boxes are assigned levels in the following manner. The root box is given level . When a sub-box of level is split, the child with the smaller fraction of the golden-section split receives level ; all other children receive level . The box with the better function value is given the larger fraction of the splitting interval and the smaller level because then it is more likely to be split again more quickly. We see that after the initialization procedure the first level is empty and the non-split boxes have levels , so it is meaningful to choose much larger than . Note that the internal structure of nag_glopt_bnd_mcs_solve (e05jb) demands that be at least .
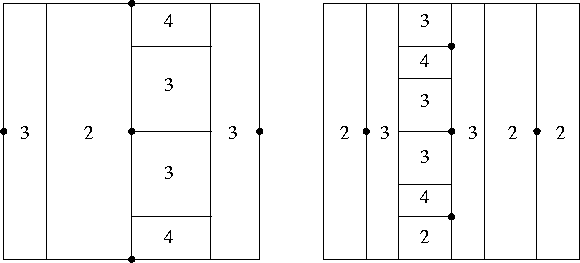
Examples of initializations in two dimensions are given in
Figure 1. In both cases the initial point is
; on the left the initialization points are
while on the right the points are
In
Figure 1, basepoints and levels after initialization are displayed. Note that these initialization lists correspond to
and
, respectively.
Figure 1: Examples of the initialization procedure
After initialization, a series of
sweeps through levels is begun. A sweep is defined by three steps:
| (i) |
scan the list of non-split sub-boxes. Fill a record list according to if there is no box at level , and with pointing to a sub-box with the lowest function value among all sub-boxes with level otherwise, for ; |
| (ii) |
the sub-box with label is a candidate for splitting. If the sub-box is not to be split, according to the rules described in Splitting, increase its level by and update if necessary. If the sub-box is split, mark it so, insert its children into the list of sub-boxes, and update if any child with level yields a strict improvement of over those sub-boxes at level ; |
| (iii) |
increment by . If then displaying monitoring information and start a new sweep; else if then repeat this step; else display monitoring information and go to the previous step. |
Clearly, each sweep ends after at most visits of the third step.
Splitting
Each sub-box is stored by
nag_glopt_bnd_mcs_solve (e05jb) as a set of information about the history of the sub-box: the label of its parent, a label identifying which child of the parent it is, etc. Whenever a sub-box
of level
is a candidate for splitting, as described in
Initialization and Sweeps, we recover
,
, and the number,
, of times coordinate
has been split in the history of
. Sub-box
could be split in one of two ways.
| (i) |
Splitting by rank
If , the box is always split. The splitting index is set to a coordinate such that . |
| (ii) |
Splitting by expected gain
If , the sub-box could be split along a coordinate where a maximal gain in function value is expected. This gain is estimated according to a local separable quadratic model obtained by fitting to function values. If the expected gain is too small the sub-box is not split at all, and its level is increased by . |
Eventually, a sub-box that is not eligible for splitting by expected gain will reach level and then be split by rank, as long as is large enough. As , the rule for splitting by rank ensures that each coordinate is split arbitrarily often.
Before describing the details of each splitting method, we introduce the procedure for correctly handling splitting at adaptive points and for dealing with unbounded intervals. Suppose we want to split the
th coordinate interval
, where we define
, for
and
, and where
is the basepoint of the sub-box being considered. The descendants of the sub-box should shrink sufficiently fast, so we should not split too close to
. Moreover, if
is large we want the new
splitting value to
not be too large, so we force it to belong to some smaller interval
, determined by
where the function
is defined by
Splitting by rank
Consider a sub-box with level . Although the sub-box has reached a high level, there is at least one coordinate along which it has not been split very often. Among the such that for , select the splitting index to be the coordinate with the lowest (and hence highest variability rank). ‘Splitting by rank’ refers to the ranking of the coordinates by and .
If
, so that
has never been split along coordinate
, the splitting is done according to the initialization list and the adaptively chosen golden-section split points, as described in
Initialization and Sweeps. Also as covered there, new basepoints and opposite points are generated. The children having the smaller fraction of the golden-section split (that is, those with larger function values) are given level
. All other children are given level
.
Otherwise, ranges between and in the th coordinate direction. The splitting value is selected to be ; we are not attempting to split based on a large reduction in function value, merely in order to reduce the size of a large interval, so may not be optimal. Sub-box is split at and the golden-section split point, producing three parts and requiring only one additional function evaluation, at the point obtained from by changing the th coordinate to . The child with the smaller fraction of the golden-section split is given level , while the other two parts are given level . Basepoints are assigned as follows: the basepoint of the first child is taken to be , and the basepoint of the second and third children is the point . Opposite points are obtained by changing to the other end of the th coordinate-interval of the corresponding child.
Splitting by expected gain
When a sub-box has level , we compute the optimal splitting index and splitting value from a local separable quadratic used as a simple local approximation of the objective function. To fit this curve, for each coordinate we need two additional points and their function values. Such data may be recoverable from the history of : whenever the th coordinate was split in the history of , we obtained values that can be used for the current quadratic interpolation in coordinate .
We loop over
; for each coordinate we pursue the history of
back to the root box, and we take the first two points and function values we find, since these are expected to be closest to the current basepoint
. If the current coordinate has not yet been split we use the initialization list. Then we generate a local separable model
for
by interpolation at
and the
additional points just collected:
We define the
expected gain in function value when we evaluate at a new point obtained by changing coordinate
in the basepoint, for each
, based on two cases:
| (i) |
. We compute the expected gain as
Again, we split according to the initialization list, with the new basepoints and opposite points being as before. |
| (ii) |
. Now, the th component of our sub-box ranges from to . Using the quadratic partial correction function
we can approximate the maximal gain expected when changing only. We will choose the splitting value from . We compute
and call the minimizer in .
If the expected best function value satisfies
where is the current best function value (including those function values obtained by local optimization), we expect the sub-box to contain a better point and so we split it, using as splitting index the component with minimal . Equation (1) prevents wasting function calls by avoiding splitting sub-boxes whose basepoints have bad function values. These sub-boxes will eventually be split by rank anyway. We now have a splitting index and a splitting value . The sub-box is split at as long as , and at the golden-section split point; two or three children are produced. The larger fraction of the golden-section split receives level , while the smaller fraction receives level . If it is the case that and the third child is larger than the smaller of the two children from the golden-section split, the third child receives level . Otherwise it is given the level . The basepoint of the first child is set to , and the basepoint of the second (and third if it exists) is obtained by changing the th coordinate of to . The opposite points are again derived by changing to the other end of the th coordinate interval of .
If equation (1) does not hold, we expect no improvement. We do not split, and we increase the level of by . |
Local Search
The local optimization algorithm used by
nag_glopt_bnd_mcs_solve (e05jb) uses linesearches along directions that are determined by minimizing quadratic models, all subject to bound constraints. Triples of vectors are computed using
coordinate searches based on linesearches. These triples are used in
triple search procedures to build local quadratic models for
. A trust-region-type approach to minimize these models is then carried out, and more information about the coordinate search and the triple search can be found in
Huyer and Neumaier (1999).
The local search starts by looking for better points without being too local, by making a triple search using points found by a coordinate search. This yields a new point and function value, an approximation of the gradient of the objective, and an approximation of the Hessian of the objective. Then the quadratic model for is minimized over a small box, with the solution to that minimization problem then being used as a linesearch direction to minimize the objective. A measure is computed to quantify the predictive quality of the quadratic model.
The third stage is the checking of termination criteria. The local search will stop if more than
visits to this part of the local search have occurred, where
is the value of the optional parameter
Local Searches Limit. If that is not the case, it will stop if the limit on function calls has been exceeded (see the description of the optional parameter
Function Evaluations Limit). The final criterion checks if no improvement can be made to the function value, or whether the approximated gradient
is small, in the sense that
The vector
is the best point at the start of the current loop in this iterative local-search procedure, the constant
is the value of the optional parameter
Local Searches Tolerance,
is the objective value at
, and
is the smallest function value found by the initialization procedure.
Next, nag_glopt_bnd_mcs_solve (e05jb) attempts to move away from the boundary, if any components of the current point lie there, using linesearches along the offending coordinates. Local searches are terminated if no improvement could be made.
The fifth stage carries out another triple search, but this time it does not use points from a coordinate search, rather points lying within the trust-region box are taken.
The final stage modifies the trust-region box to be bigger or smaller, depending on the quality of the quadratic model, minimizes the new quadratic model on that box, and does a linesearch in the direction of the minimizer. The value of is updated using the new data, and then we go back to the third stage (checking of termination criteria).
The Hessians of the quadratic models generated by the local search may not be positive definite, so
nag_glopt_bnd_mcs_solve (e05jb) uses the general nonlinear optimizer
nag_opt_nlp2_sparse_solve (e04vh) to minimize the models.
Optional Parameters
Several optional parameters in nag_glopt_bnd_mcs_solve (e05jb) define choices in the problem specification or the algorithm logic. In order to reduce the number of formal arguments of nag_glopt_bnd_mcs_solve (e05jb) these optional parameters have associated default values that are appropriate for most problems. Therefore, you need only specify those optional parameters whose values are to be different from their default values.
The remainder of this section can be skipped if you wish to use the default values for all optional parameters.
The following is a list of the optional parameters available. A full description of each optional parameter is provided in
Description of the s.
All optional parameters not specified by you are set to their default values. Valid values of optional parameters specified by you are unaltered by nag_glopt_bnd_mcs_solve (e05jb) and so remain in effect for subsequent calls to nag_glopt_bnd_mcs_solve (e05jb), unless you explicitly change them.
Description of the Optional Parameters
For each option, we give a summary line, a description of the optional parameter and details of constraints.
The summary line contains:
- a parameter value,
where the letters , and denote options that take character, integer and real values respectively, and where the letter denotes an option that takes an or value;
- the default value, where the symbol is a generic notation for machine precision (see nag_machine_precision (x02aj)), the symbol stands for the largest positive model number (see nag_machine_real_largest (x02al)), represents the number of non-fixed variables, and the symbol stands for the maximum number of decimal digits that can be represented (see nag_machine_decimal_digits (x02be)).
Option names are case-insensitive and must be provided in full; abbreviations are not recognized.
Defaults
This special keyword is used to reset all optional parameters to their default values, and any random state stored in the array
comm will be destroyed.
Any option value given with this keyword will be ignored. This optional parameter cannot be queried or got.
Function Evaluations Limit Default
This puts an approximate limit on the number of function calls allowed. The total number of calls made is checked at the top of an internal iteration loop, so it is possible that a few calls more than may be made.
Constraint:
.
Infinite Bound Size Default
This defines the ‘infinite’ bound in the definition of the problem constraints. Any upper bound greater than or equal to will be regarded as (and similarly any lower bound less than or equal to will be regarded as ).
Constraint:
.
Local Searches Default
If you want to try to accelerate convergence of nag_glopt_bnd_mcs_solve (e05jb) by starting local searches from candidate minima, you will require to be .
Constraint:
.
Local Searches Limit Default
This defines the maximal number of iterations to be used in the trust-region loop of the local-search procedure.
Constraint:
.
Local Searches Tolerance Default
The value of
is the multiplier used during local searches as a stopping criterion for when the approximated gradient is small, in the sense described in
Local Search.
Constraint:
.
Minimize Default
Maximize
These keywords specify the required direction of optimization. Any option value given with these keywords will be ignored.
Nolist Default
List
These options control the echoing of each optional parameter specification as it is supplied.
List turns printing on,
Nolist turns printing off. The output is sent to the current advisory message unit (as defined by
nag_file_set_unit_advisory (x04ab)).
Any option value given with these keywords will be ignored. This optional parameter cannot be queried or got.
Repeatability Default
For use with random initialization lists (
). When set to
, an internally-initialized random state is stored in the array
comm for use in subsequent calls to
nag_glopt_bnd_mcs_solve (e05jb).
Constraint:
.
Splits Limit Default
Along with the initialization list
list, this defines a limit on the number of times the root box will be split along any single coordinate direction. If
Local Searches is
you may find the default value to be too small.
Constraint:
.
Static Limit Default
As the default termination criterion, computation stops when the best function value is static for
sweeps through levels. This parameter is ignored if you have specified a target value to reach in
Target Objective Value.
Constraint:
.
Target Objective Error Default
If you have given a target objective value to reach in
(the value of the optional parameter
Target Objective Value),
sets your desired relative error (from above if
Minimize is set, from below if
Maximize is set) between
obj and
, as described in
Accuracy. See also the description of the optional parameter
Target Objective Safeguard.
Constraint:
.
Target Objective Safeguard Default
If you have given a target objective value to reach in
(the value of the optional parameter
Target Objective Value),
sets your desired safeguarded termination tolerance, for when
is close to zero.
Constraint:
.
Target Objective Value
This parameter may be set if you wish
nag_glopt_bnd_mcs_solve (e05jb) to use a specific value as the target function value to reach during the optimization. Setting
overrides the default termination criterion determined by the optional parameter
Static Limit.
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015