PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_fit_2dspline_panel (e02da)
Purpose
nag_fit_2dspline_panel (e02da) forms a minimal, weighted least squares bicubic spline surface fit with prescribed knots to a given set of data points.
Syntax
[
lamda,
mu,
dl,
c,
sigma,
rank,
ifail] = e02da(
x,
y,
f,
w,
lamda,
mu,
point,
eps, 'm',
m, 'px',
px, 'py',
py, 'npoint',
npoint)
[
lamda,
mu,
dl,
c,
sigma,
rank,
ifail] = nag_fit_2dspline_panel(
x,
y,
f,
w,
lamda,
mu,
point,
eps, 'm',
m, 'px',
px, 'py',
py, 'npoint',
npoint)
Description
nag_fit_2dspline_panel (e02da) determines a bicubic spline fit
to the set of data points
with weights
, for
. The two sets of internal knots of the spline,
and
, associated with the variables
and
respectively, are prescribed by you. These knots can be thought of as dividing the data region of the
plane into panels (see
Figure 1 in
Arguments). A bicubic spline consists of a separate bicubic polynomial in each panel, the polynomials joining together with continuity up to the second derivative across the panel boundaries.
has the property that
, the sum of squares of its weighted residuals
, for
, where
is as small as possible for a bicubic spline with the given knot sets. The function produces this minimized value of
and the coefficients
in the B-spline representation of
– see
Further Comments.
nag_fit_2dspline_evalv (e02de),
nag_fit_2dspline_evalm (e02df) and
nag_fit_2dspline_derivm (e02dh) are available to compute values and derivatives of the fitted spline from the coefficients
.
The least squares criterion is not always sufficient to determine the bicubic spline uniquely: there may be a whole family of splines which have the same minimum sum of squares. In these cases, the function selects from this family the spline for which the sum of squares of the coefficients
is smallest: in other words, the minimal least squares solution. This choice, although arbitrary, reduces the risk of unwanted fluctuations in the spline fit. The method employed involves forming a system of
linear equations in the coefficients
and then computing its least squares solution, which will be the minimal least squares solution when appropriate. The basis of the method is described in
Hayes and Halliday (1974). The matrix of the equation is formed using a recurrence relation for B-splines which is numerically stable (see
Cox (1972) and
de Boor (1972) – the former contains the more elementary derivation but, unlike
de Boor (1972), does not cover the case of coincident knots). The least squares solution is also obtained in a stable manner by using orthogonal transformations, viz. a variant of Givens rotation (see
Gentleman (1973)). This requires only one row of the matrix to be stored at a time. Advantage is taken of the stepped-band structure which the matrix possesses when the data points are suitably ordered, there being at most sixteen nonzero elements in any row because of the definition of B-splines. First the matrix is reduced to upper triangular form and then the diagonal elements of this triangle are examined in turn. When an element is encountered whose square, divided by the mean squared weight, is less than a threshold
, it is replaced by zero and the rest of the elements in its row are reduced to zero by rotations with the remaining rows. The rank of the system is taken to be the number of nonzero diagonal elements in the final triangle, and the nonzero rows of this triangle are used to compute the minimal least squares solution. If all the diagonal elements are nonzero, the rank is equal to the number of coefficients
and the solution obtained is the ordinary least squares solution, which is unique in this case.
References
Cox M G (1972) The numerical evaluation of B-splines J. Inst. Math. Appl. 10 134–149
de Boor C (1972) On calculating with B-splines J. Approx. Theory 6 50–62
Gentleman W M (1973) Least squares computations by Givens transformations without square roots J. Inst. Math. Applic. 12 329–336
Hayes J G and Halliday J (1974) The least squares fitting of cubic spline surfaces to general data sets J. Inst. Math. Appl. 14 89–103
Parameters
Compulsory Input Parameters
- 1:
– double array
- 2:
– double array
- 3:
– double array
-
The coordinates of the data point
, for
. The order of the data points is immaterial, but see the array
point.
- 4:
– double array
-
The weight
of the
th data point. It is important to note the definition of weight implied by the equation
(1) in
Description, since it is also common usage to define weight as the square of this weight. In this function, each
should be chosen inversely proportional to the (absolute) accuracy of the corresponding
, as expressed, for example, by the standard deviation or probable error of the
. When the
are all of the same accuracy, all the
may be set equal to
.
- 5:
– double array
-
must contain the
th interior knot
associated with the variable
, for
. The knots must be in nondecreasing order and lie strictly within the range covered by the data values of
. A knot is a value of
at which the spline is allowed to be discontinuous in the third derivative with respect to
, though continuous up to the second derivative. This degree of continuity can be reduced, if you require, by the use of coincident knots, provided that no more than four knots are chosen to coincide at any point. Two, or three, coincident knots allow loss of continuity in, respectively, the second and first derivative with respect to
at the value of
at which they coincide. Four coincident knots split the spline surface into two independent parts. For choice of knots see
Further Comments.
- 6:
– double array
-
must contain the th interior knot associated with the variable , for .
- 7:
– int64int32nag_int array
-
Indexing information usually provided by
nag_fit_2dspline_sort (e02za) which enables the data points to be accessed in the order which produces the advantageous matrix structure mentioned in
Description. This order is such that, if the
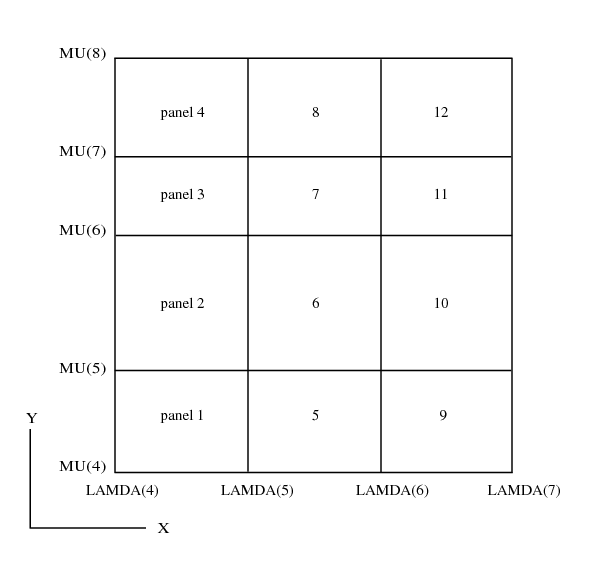
plane is thought of as being divided into rectangular panels by the two sets of knots, all data in a panel occur before data in succeeding panels, where the panels are numbered from bottom to top and then left to right with the usual arrangement of axes, as indicated in
Figure 1.
Figure 1
A data point lying exactly on one or more panel sides is considered to be in the highest numbered panel adjacent to the point.
nag_fit_2dspline_sort (e02za) should be called to obtain the array
point, unless it is provided by other means.
- 8:
– double scalar
-
A threshold
for determining the effective rank of the system of linear equations. The rank is determined as the number of elements of the array
dl which are nonzero. An element of
dl is regarded as zero if it is less than
.
Machine precision is a suitable value for
in most practical applications which have only
or
decimals accurate in data. If some coefficients of the fit prove to be very large compared with the data ordinates, this suggests that
should be increased so as to decrease the rank. The array
dl will give a guide to appropriate values of
to achieve this, as well as to the choice of
in other cases where some experimentation may be needed to determine a value which leads to a satisfactory fit.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the arrays
x,
y,
f,
w. (An error is raised if these dimensions are not equal.)
, the number of data points.
Constraint:
.
- 2:
– int64int32nag_int scalar
- 3:
– int64int32nag_int scalar
-
Default:
For
px, the dimension of the array
lamda. For
py, the dimension of the array
mu.
The total number of knots and associated with the variables and , respectively.
Constraint:
and
.
(They are such that
and
are the corresponding numbers of interior knots.) The running time and storage required by the function are both minimized if the axes are labelled so that
py is the smaller of
px and
py.
- 4:
– int64int32nag_int scalar
-
Default:
the dimension of the array
point.
The dimension of the array
point.
Constraint:
.
Output Parameters
- 1:
– double array
-
The interior knots
to
are unchanged, and the segments
and
contain additional (exterior) knots introduced by the function in order to define the full set of B-splines required. The four knots in the first segment are all set equal to the lowest data value of
and the other four additional knots are all set equal to the highest value: there is experimental evidence that coincident end-knots are best for numerical accuracy. The complete array must be left undisturbed if
nag_fit_2dspline_evalv (e02de) or
nag_fit_2dspline_evalm (e02df) is to be used subsequently.
- 2:
– double array
-
The same remarks apply to
mu as to
lamda above, with
y replacing
x, and
replacing
.
- 3:
– double array
-
.
Gives the squares of the diagonal elements of the reduced triangular matrix, divided by the mean squared weight. It includes those elements, less than
, which are treated as zero (see
Description).
- 4:
– double array
-
.
Gives the coefficients of the fit.
is the coefficient
of
Description and
Further Comments, for
and
. These coefficients are used by
nag_fit_2dspline_evalv (e02de) or
nag_fit_2dspline_evalm (e02df) to calculate values of the fitted function.
- 5:
– double scalar
-
, the weighted sum of squares of residuals. This is not computed from the individual residuals but from the right-hand sides of the orthogonally-transformed linear equations. For further details see page 97 of
Hayes and Halliday (1974). The two methods of computation are theoretically equivalent, but the results may differ because of rounding error.
- 6:
– int64int32nag_int scalar
-
The rank of the system as determined by the value of the threshold
.
- The least squares solution is unique.
- The minimal least squares solution is computed.
- 7:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
At least one set of knots is not in nondecreasing order, or an interior knot is outside the range of the data values.
-
-
More than four knots coincide at a single point, possibly because all data points have the same value of (or ) or because an interior knot coincides with an extreme data value.
-
-
Array
point does not indicate the data points in panel order. Call
nag_fit_2dspline_sort (e02za) to obtain a correct array.
-
-
| On entry, | , |
| or | , |
| or | , |
| or | , |
| or | nws is too small, |
| or | npoint is too small. |
-
-
All the weights are zero or rank determined as zero.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
The computation of the B-splines and reduction of the observation matrix to triangular form are both numerically stable.
Further Comments
The time taken is approximately proportional to the number of data points, , and to .
The B-spline representation of the bicubic spline is
summed over
and over
. Here
and
denote normalized cubic B-splines, the former defined on the knots
and the latter on the knots
. For further details, see
Hayes and Halliday (1974) for bicubic splines and
de Boor (1972) for normalized B-splines.
The choice of the interior knots, which help to determine the spline's shape, must largely be a matter of trial and error. It is usually best to start with a small number of knots and, examining the fit at each stage, add a few knots at a time in places where the fit is particularly poor. In intervals of or where the surface represented by the data changes rapidly, in function value or derivatives, more knots will be needed than elsewhere. In some cases guidance can be obtained by analogy with the case of coincident knots: for example, just as three coincident knots can produce a discontinuity in slope, three close knots can produce rapid change in slope. Of course, such rapid changes in behaviour must be adequately represented by the data points, as indeed must the behaviour of the surface generally, if a satisfactory fit is to be achieved. When there is no rapid change in behaviour, equally-spaced knots will often suffice.
In all cases the fit should be examined graphically before it is accepted as satisfactory.
The fit obtained is not defined outside the rectangle
The reason for taking the extreme data values of
and
for these four knots is that, as is usual in data fitting, the fit cannot be expected to give satisfactory values outside the data region. If, nevertheless, you require values over a larger rectangle, this can be achieved by augmenting the data with two artificial data points
and
with zero weight, where
,
defines the enlarged rectangle. In the case when the data are adequate to make the least squares solution unique (
), this enlargement will not affect the fit over the original rectangle, except for possibly enlarged rounding errors, and will simply continue the bicubic polynomials in the panels bordering the rectangle out to the new boundaries: in other cases the fit will be affected. Even using the original rectangle there may be regions within it, particularly at its corners, which lie outside the data region and where, therefore, the fit will be unreliable. For example, if there is no data point in panel
of
Figure 1 in
Arguments, the least squares criterion leaves the spline indeterminate in this panel: the minimal spline determined by the function in this case passes through the value zero at the point
.
Example
This example reads a value for
, and a set of data points, weights and knot positions. If there are more
knots than
knots, it interchanges the
and
axes. It calls
nag_fit_2dspline_sort (e02za) to sort the data points into panel order,
nag_fit_2dspline_panel (e02da) to fit a bicubic spline to them, and
nag_fit_2dspline_evalv (e02de) to evaluate the spline at the data points.
Finally it prints:
| – |
the weighted sum of squares of residuals computed from the linear equations; |
| – |
the rank determined by nag_fit_2dspline_panel (e02da); |
| – |
data points, fitted values and residuals in panel order; |
| – |
the weighted sum of squares of the residuals; and |
| – |
the coefficients of the spline fit. |
The program is written to handle any number of datasets.
Note: the data supplied in this example is
not typical of a realistic problem: the number of data points would normally be much larger (in which case the array dimensions and the value of
nws in the program would have to be increased); and the value of
would normally be much smaller on most machines (see
Arguments; the relatively large value of
has been chosen in order to illustrate a minimal least squares solution when
; in this example
).
Open in the MATLAB editor:
e02da_example
function e02da_example
fprintf('e02da example results\n\n');
npts = 30;
x = [ 0.60 -0.95 0.87 0.84 0.17 -0.87 1.00 0.10 0.24 -0.77 ...
0.32 1.00 -0.63 -0.66 0.93 0.15 0.99 -0.54 0.44 -0.72 ...
0.63 -0.40 0.20 0.43 0.28 -0.24 0.86 -0.41 -0.05 -1.00];
y = [-0.52 -0.61 0.93 0.09 0.88 -0.70 1.00 1.00 0.30 -0.77 ...
-0.23 -1.00 -0.26 -0.83 0.22 0.89 -0.80 -0.88 0.68 -0.14 ...
0.67 -0.90 -0.84 0.84 0.15 -0.91 -0.35 -0.16 -0.35 -1.00];
f = [ 0.93 -1.79 0.36 0.52 0.49 -1.76 0.33 0.48 0.65 -1.82 ...
0.92 1.00 8.88 -2.01 0.47 0.49 0.84 -2.42 0.47 7.15 ...
0.44 -3.34 2.78 0.44 0.70 -6.52 0.66 2.32 1.66 -1.00];
npts = size(x,2);
w = ones(npts,1);
w(1:6) = 10;
px = 10;
lamda = zeros(px,1);
lamda(5) = -0.5;
py = 8;
mu = zeros(py, 1);
epsilon = 1e-06;
[point, ifail] = e02za( ...
lamda, mu, x, y);
fprintf('Interior x-knots:\n');
if px==8
fprintf('None');
else
fprintf('%10.4f',lamda(5:px-4));
end
fprintf('\n\nInterior y-knots:\n');
if py==8
fprintf('None');
else
fprintf('%10.4f',mu(5:py-4));
end
fprintf('\n');
[lamda, mu, dl, c, sigma, rank, ifail] = ...
e02da(...
x, y, f, w, lamda, mu, point, epsilon);
fprintf('\nSum of squares of residual RHS = %16.2e\n\n', sigma);
fprintf('Rank = %5d\n\n',rank);
[ff, ifail] = e02de( ...
x, y, lamda, mu, c);
res = ff'-f;
fprintf('Spline evaluated at original data points\n');
fprintf(' x y f fit residual\n');
fprintf('%11.4f%11.4f%11.4f%11.4f%11.2e\n',[x; y; f; ff'; res]);
wres = res.*w';
sres = dot(wres,wres);
fprintf('\nSum of squared weighted residuals = %16.2e\n\n',sres)
fprintf('Spline coefficients:\n');
c = reshape(c,[px-4,py-4]);
disp(c);
xm = [-0.95:0.05:0.95]; ym = xm;
nn = size(xm,2);
for i = 1:nn
xx = xm(i)*ones(1,nn);
[fit(:,i), ifail] = e02de( ...
xx, ym, lamda, mu, c);
end
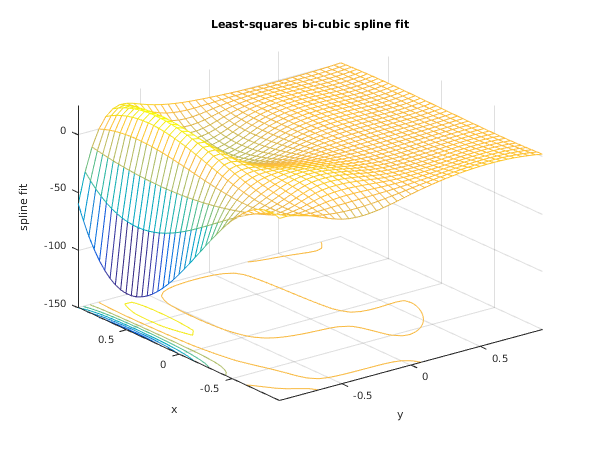
fig1 = figure;
meshc(xm,ym,fit);
title('Least-squares bi-cubic spline fit');
xlabel('y');
ylabel('x');
zlabel('spline fit');
e02da example results
Interior x-knots:
-0.5000 0.0000
Interior y-knots:
None
Sum of squares of residual RHS = 1.47e+01
Rank = 22
Spline evaluated at original data points
x y f fit residual
0.6000 -0.5200 0.9300 0.9441 1.41e-02
-0.9500 -0.6100 -1.7900 -1.7931 -3.13e-03
0.8700 0.9300 0.3600 0.3529 -7.10e-03
0.8400 0.0900 0.5200 0.5024 -1.76e-02
0.1700 0.8800 0.4900 0.4705 -1.95e-02
-0.8700 -0.7000 -1.7600 -1.7521 7.89e-03
1.0000 1.0000 0.3300 0.6315 3.01e-01
0.1000 1.0000 0.4800 1.4910 1.01e+00
0.2400 0.3000 0.6500 0.9241 2.74e-01
-0.7700 -0.7700 -1.8200 -2.4301 -6.10e-01
0.3200 -0.2300 0.9200 -0.3692 -1.29e+00
1.0000 -1.0000 1.0000 1.0835 8.35e-02
-0.6300 -0.2600 8.8800 7.6346 -1.25e+00
-0.6600 -0.8300 -2.0100 -1.5815 4.28e-01
0.9300 0.2200 0.4700 1.4912 1.02e+00
0.1500 0.8900 0.4900 0.4414 -4.86e-02
0.9900 -0.8000 0.8400 0.5495 -2.90e-01
-0.5400 -0.8800 -2.4200 -2.6795 -2.60e-01
0.4400 0.6800 0.4700 1.5862 1.12e+00
-0.7200 -0.1400 7.1500 7.5708 4.21e-01
0.6300 0.6700 0.4400 0.6288 1.89e-01
-0.4000 -0.9000 -3.3400 -4.6955 -1.36e+00
0.2000 -0.8400 2.7800 1.7123 -1.07e+00
0.4300 0.8400 0.4400 0.6888 2.49e-01
0.2800 0.1500 0.7000 0.7713 7.13e-02
-0.2400 -0.9100 -6.5200 -4.7072 1.81e+00
0.8600 -0.3500 0.6600 0.9347 2.75e-01
-0.4100 -0.1600 2.3200 2.7039 3.84e-01
-0.0500 -0.3500 1.6600 2.2865 6.26e-01
-1.0000 -1.0000 -1.0000 -1.0228 -2.28e-02
Sum of squared weighted residuals = 1.47e+01
Spline coefficients:
-1.0228 258.5042 9.9575 -15.3533
115.4668 15.6756 -51.6200 -0.3260
-433.5558 -29.4878 67.6666 1.0835
-68.1973 132.2933 -5.8765 -2.7932
24.8426 -173.5103 10.0577 7.7708
-140.1485 20.0983 4.7543 0.6315
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015