PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_ode_ivp_2nd_rkn (d02la)
Purpose
nag_ode_ivp_2nd_rkn (d02la) is a function for integrating a non-stiff system of second-order ordinary differential equations using Runge–Kutta–Nystrom techniques.
Syntax
[
t,
y,
yp,
ydp,
rwork,
ifail] = d02la(
fcn,
t,
tend,
y,
yp,
ydp,
rwork, 'neq',
neq)
[
t,
y,
yp,
ydp,
rwork,
ifail] = nag_ode_ivp_2nd_rkn(
fcn,
t,
tend,
y,
yp,
ydp,
rwork, 'neq',
neq)
Note: the interface to this routine has changed since earlier releases of the toolbox:
| At Mark 22: |
lrwork was removed from the interface |
Description
Given the initial values
nag_ode_ivp_2nd_rkn (d02la) integrates a non-stiff system of second-order differential equations of the type
from
to
using a Runge–Kutta–Nystrom formula pair. The system is defined by
fcn, which evaluates
in terms of
and
, where
are supplied at
.
There are two Runge–Kutta–Nystrom formula pairs implemented in this function. The lower order method is intended if you have moderate accuracy requirements and may be used in conjunction with the interpolation function
nag_ode_ivp_2nd_rkn_interp (d02lz) to produce solutions and derivatives at user-specified points. The higher order method is intended if you have high accuracy requirements.
In one-step mode the function returns approximations to the solution, derivative and
at each integration point. In interval mode these values are returned at the end of the integration range. You select the order of the method, the mode of operation, the error control and various optional inputs by a prior call to
nag_ode_ivp_2nd_rkn_setup (d02lx).
For a description of the Runge–Kutta–Nystrom formula pairs see
Dormand et al. (1986a) and
Dormand et al. (1986b) and for a description of their practical implementation see
Brankin et al. (1989).
References
Brankin R W, Dormand J R, Gladwell I, Prince P J and Seward W L (1989) Algorithm 670: A Runge–Kutta–Nystrom Code ACM Trans. Math. Software 15 31–40
Dormand J R, El–Mikkawy M E A and Prince P J (1986a) Families of Runge–Kutta–Nystrom formulae Mathematical Report TPMR 86-1 Teesside Polytechnic
Dormand J R, El–Mikkawy M E A and Prince P J (1986b) High order embedded Runge–Kutta–Nystrom formulae Mathematical Report TPMR 86-2 Teesside Polytechnic
Parameters
Compulsory Input Parameters
- 1:
– function handle or string containing name of m-file
-
fcn must evaluate the functions
(that is the second derivatives
) for given values of its arguments
,
.
[f] = fcn(neq, t, y)
Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of differential equations.
- 2:
– double scalar
-
, the value of the argument.
- 3:
– double array
-
, for , the value of the argument.
Output Parameters
- 1:
– double array
-
The value of
, for .
- 2:
– double scalar
-
The initial value of the independent variable .
Constraint:
.
- 3:
– double scalar
-
The end point of the range of integration. If
on initial entry, integration will proceed in the negative direction.
tend may be reset, in the direction of integration, before any continuation call.
- 4:
– double array
-
The initial values of the solution .
- 5:
– double array
-
The initial values of the derivatives .
- 6:
– double array
-
Must be unchanged from a previous call to nag_ode_ivp_2nd_rkn (d02la).
- 7:
– double array
-
This
must be the same argument
rwork as supplied to
nag_ode_ivp_2nd_rkn_setup (d02lx). It is used to pass information from
nag_ode_ivp_2nd_rkn_setup (d02lx) to
nag_ode_ivp_2nd_rkn (d02la), and from
nag_ode_ivp_2nd_rkn (d02la) to both
nag_ode_ivp_2nd_rkn_diag (d02ly) and
nag_ode_ivp_2nd_rkn_interp (d02lz). Therefore the contents of this array
must not be changed before the call to
nag_ode_ivp_2nd_rkn (d02la) or calling either of the functions
nag_ode_ivp_2nd_rkn_diag (d02ly) and
nag_ode_ivp_2nd_rkn_interp (d02lz).
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the arrays
y,
yp,
ydp. (An error is raised if these dimensions are not equal.)
The number of second-order ordinary differential equations to be solved by
nag_ode_ivp_2nd_rkn (d02la). It must contain the same value as the argument
neq used in a prior call to
nag_ode_ivp_2nd_rkn_setup (d02lx).
Constraint:
.
Output Parameters
- 1:
– double scalar
-
The value of the independent variable, which is usually
tend, unless an error has occurred or the code is operating in one-step mode. If the integration is to be continued, possibly with a new value for
tend,
t must not be changed.
- 2:
– double array
-
The computed values of the solution at the exit value of
t. If the integration is to be continued, possibly with a new value for
tend, these values must not be changed.
- 3:
– double array
-
The computed values of the derivatives at the exit value of
t. If the integration is to be continued, possibly with a new value for
tend, these values must not be changed.
- 4:
– double array
-
The computed values of the second derivative at the exit value of
t, unless illegal input is detected, in which case the elements of
ydp may not have been initialized. If the integration is to be continued, possibly with a new value for
tend, these values must not be changed.
- 5:
– double array
-
- 6:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
Illegal input detected, i.e., one of the following conditions:
This error exit can be caused if elements of
rwork have been overwritten.
-
-
The maximum number of steps has been attempted. (See argument
maxstp in
nag_ode_ivp_2nd_rkn_setup (d02lx).) If integration is to be continued then you need only reset
ifail and call the function again and a further
maxstp steps will be attempted.
-
-
In order to satisfy the error requirements, the step size needed is too small for the
machine precision being used.
-
-
The code has detected two successive error exits at the current value of and cannot proceed. Check all input variables.
-
-
The code has detected inefficient use of the integration method. The step size has been reduced by a significant amount too often in order to hit the output points specified by
tend. (Of the last
or more successful steps more than
are steps with sizes that have had to be reduced by a factor of greater than a half.)
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
The accuracy of integration is determined by the arguments
tol,
thres and
thresp in a prior call to
nag_ode_ivp_2nd_rkn_setup (d02lx). Note that only the local error at each step is controlled by these arguments. The error estimates obtained are not strict bounds but are usually reliable over one step. Over a number of steps the overall error may accumulate in various ways, depending on the system. The code is designed so that a reduction in
tol should lead to an approximately proportional reduction in the error. You are strongly recommended to call
nag_ode_ivp_2nd_rkn (d02la) with more than one value for
tol and to compare the results obtained to estimate their accuracy.
The accuracy obtained depends on the type of error test used. If the solution oscillates around zero a relative error test should be avoided, whereas if the solution is exponentially increasing an absolute error test should not be used. For a description of the error test see the specifications of the arguments
tol,
thres and
thresp in function document
nag_ode_ivp_2nd_rkn_setup (d02lx).
Further Comments
If
nag_ode_ivp_2nd_rkn (d02la) fails with
then the value of
tol may be so small that a solution cannot be obtained, in which case the function should be called again with a larger value for
tol. If the accuracy requested is really needed then you should consider whether there is a more fundamental difficulty. For example:
| (a) |
in the region of a singularity the solution components will usually be of a large magnitude. nag_ode_ivp_2nd_rkn (d02la) could be used in one-step mode to monitor the size of the solution with the aim of trapping the solution before the singularity. In any case numerical integration cannot be continued through a singularity, and analytical treatment may be necessary; |
| (b) |
if the solution contains fast oscillatory components, the function will require a very small step size to preserve stability. This will usually be exhibited by excessive computing time and sometimes an error exit with . The Runge–Kutta–Nystrom methods are not efficient in such cases and you should consider reposing your problem as a system of first-order ordinary differential equations and then using a function from Sub-chapter D02M–N with the Blend formulae (see nag_ode_ivp_stiff_dassl (d02mv)). |
nag_ode_ivp_2nd_rkn (d02la) can be used for producing results at short intervals (for example, for tabulation), in two ways. By far the less efficient is to call
nag_ode_ivp_2nd_rkn (d02la) successively over short intervals,
to
, although this is the only way if the higher order method has been selected and precisely
not what it is intended for. A more efficient way,
only for use when the lower order method has been selected, is to use
nag_ode_ivp_2nd_rkn (d02la) in one-step mode. The output values of arguments
y,
yp,
ydp,
t and
rwork are set correctly for a call to
nag_ode_ivp_2nd_rkn_interp (d02lz) to compute the solution and derivative at the required points.
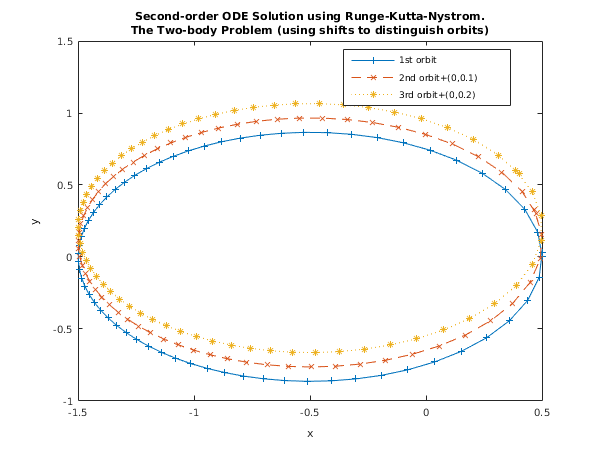
Example
This example solves the following system (the two body problem)
over the range
with initial conditions
,
,
and
where
, the eccentricity, is
. The system is solved using the lower order method with relative local error tolerances
and
and default threshold tolerances.
nag_ode_ivp_2nd_rkn (d02la) is used in one-step mode (
) and
nag_ode_ivp_2nd_rkn_interp (d02lz) provides solution values at intervals of
.
Open in the MATLAB editor:
d02la_example
function d02la_example
fprintf('d02la example results\n\n');
ecc = 0.5;
tend = 20;
tstart = 0;
tinc = 0.1;
neq = 2;
lrwork = 16+20*neq;
nwant = neq;
thres = zeros(neq, 1);
thresp = zeros(neq, 1);
fprintf('d02la example program results \n\n');
for itol = 4:5
tol = 10^(-itol);
thres(1) = 0.0;
thresp(1) = 0.0;
h = 0.0;
maxstp = 0;
start = true;
high = false;
onestp = true;
rwork = zeros(lrwork,1);
t = 0;
y = [1-ecc; 0];
yp = [0; sqrt((1+ecc)/(1-ecc))];
ydp = zeros(neq, 1);
[start, rwork, ifail] = d02lx(h, tol, thres, thresp, int64(maxstp),...
start, onestp, high, rwork, 'neq', int64(neq));
fprintf('Calculation with tol = %1.1e \n\n',tol);
t = tstart;
tnext = t + tinc;
if itol == 4
ncall = 1;
tkeep = tnext;
ykeep = y;
nkeep = 1;
end
while (t < tend)
[tout, y, yp, ydp, rwork, ifail] = d02la(@fcn, t, tend, y,...
yp, ydp, rwork);
t = tout;
while (tnext <= t)
[ywant, ypwant, ifail] = d02lz(t, y, yp, int64(neq), tnext,...
rwork, 'neq', int64(neq));
ncall = ncall+1;
if itol == 4
tkeep(ncall) = tnext;
ykeep(:,ncall) = ywant;
end
tnext = tnext + tinc;
end
end
[hnext, hused, hstart, nsucc, nfail, natt, thres, thresp, ifail] =...
d02ly(int64(neq), rwork);
fprintf('\nNumber of successful steps = %1.0f\n',nsucc);
fprintf('Number of failed steps = %1.0f\n',nfail);
fprintf('\n\n');
end
nhalf = 1;
while ykeep(2,nhalf) >= 0
nhalf = nhalf+1;
end
fig1 = figure;
display_plot(ykeep, nhalf);
function ydp = fcn(neq, t, y)
r = sqrt(y(1)^2+y(2)^2)^3;
f = zeros(2,1);
ydp(1) = -y(1)/r;
ydp(2) = -y(2)/r;
function display_plot(ykeep, nhalf)
norb1 = 2*(nhalf-1); norb2 = 2*norb1; norb3 = 3*norb1;
plot(ykeep(1,1:norb1), ykeep(2,1:norb1), '-+', ...
ykeep(1,norb1+1:norb2), ykeep(2,norb1+1:norb2)+0.1, '--x', ...
ykeep(1,norb2+1:norb3), ykeep(2,norb2+1:norb3)+0.2, ':*');
title({'Second-order ODE Solution using Runge-Kutta-Nystrom.', ...
'The Two-body Problem (using shifts to distinguish orbits)'});
xlabel('x'); ylabel('y');
legend('1st orbit', '2nd orbit+(0,0.1)', '3rd orbit+(0,0.2)', ...
'Location', 'Best');
d02la example results
d02la example program results
Calculation with tol = 1.0e-04
Number of successful steps = 108
Number of failed steps = 16
Calculation with tol = 1.0e-05
Number of successful steps = 169
Number of failed steps = 15
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015