hide long namesshow long names
hide short namesshow short names
Integer type:  int32  int64  nag_int  show int32  show int32  show int64  show int64  show nag_int  show nag_int
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox

NAG Toolbox: nag_ode_bvp_coll_sys (d02jb)

▸▿ Contents

    1  Purpose
    2  Syntax
    3  Description
    4  References
▸▿ 5  Parameters
    6  Error Indicators and Warnings
    7  Accuracy
    8  Further Comments
    9  Example

Purpose

nag_ode_bvp_coll_sys (d02jb) solves a regular linear two-point boundary value problem for a system of ordinary differential equations by Chebyshev series using collocation and least squares.

Syntax

[c, ifail] = d02jb(n, cf, bc, x0, x1, k1, kp)
[c, ifail] = nag_ode_bvp_coll_sys(n, cf, bc, x0, x1, k1, kp)

Description

nag_ode_bvp_coll_sys (d02jb) calculates the solution of a regular two-point boundary value problem for a regular linear nth-order system of first-order ordinary differential equations as a Chebyshev series in the interval x0,x1. The differential equation
y′=Axy+rx  
is defined by cf, and the boundary conditions at the points x0 and x1 are defined by bc.
You specify the degree of Chebyshev series required, k1-1, and the number of collocation points, kp. The function sets up a system of linear equations for the Chebyshev coefficients, n equations for each collocation point and one for each boundary condition. The boundary conditions are solved exactly, and the remaining equations are then solved by a least squares method. The result produced is a set of coefficients for a Chebyshev series solution for each component of the solution of the system of differential equations on an interval normalized to -1,1.
nag_fit_1dcheb_eval2 (e02ak) can be used to evaluate the components of the solution at any point on the interval x0,x1 – see Example for an example. nag_fit_1dcheb_deriv (e02ah) followed by nag_fit_1dcheb_eval2 (e02ak) can be used to evaluate their derivatives.

References

Picken S M (1970) Algorithms for the solution of differential equations in Chebyshev-series by the selected points method Report Math. 94 National Physical Laboratory

Parameters

Compulsory Input Parameters

1:     n – int64int32nag_int scalar
n, the order of the system of differential equations.
Constraint: n≥1.
2:     cf – function handle or string containing name of m-file
cf defines the system of differential equations (see Description). It must return the value of a coefficient function ai,jx, of A, at a given point x, or of a right-hand side function rix if j=0.
[result] = cf(ii, j, x)

Input Parameters

1:     ii – int64int32nag_int scalar
2:     j – int64int32nag_int scalar
Indicate the function to be evaluated, namely ai,jx if 1≤j≤n, or rix if j=0.
1≤ii≤n, 0≤j≤n.
3:     x – double scalar
The point at which the function is to be evaluated.

Output Parameters

1:     result – double scalar
The value of a coefficient function ai,jx, of A, at a given point x, or of a right-hand side function rix if j=0.
3:     bc – function handle or string containing name of m-file
bc defines the n boundary conditions, which have the form ykx0=s or ykx1=s. The boundary conditions may be specified in any order.
[j, rhs] = bc(ii)

Input Parameters

1:     ii – int64int32nag_int scalar
The index of the boundary condition to be defined.

Output Parameters

1:     j – int64int32nag_int scalar
Must be set to -k if the ith boundary condition is ykx0=s, or to +k if it is ykx1=s.
j must not be set to the same value k for two different values of ii.
2:     rhs – double scalar
The value s.
4:     x0 – double scalar
5:     x1 – double scalar
The left- and right-hand boundaries, x0 and x1, respectively.
Constraint: x1>x0.
6:     k1 – int64int32nag_int scalar
The number of coefficients to be returned in the Chebyshev series representation of the components of the solution (hence the degree of the polynomial approximation is k1-1).
Constraint: k1≥2.
7:     kp – int64int32nag_int scalar
The number of collocation points to be used.
Constraint: kp≥k1-1.

Optional Input Parameters

None.

Output Parameters

1:     cldcn – double array
The computed Chebyshev coefficients of the kth component of the solution, yk; that is, the computed solution is:
yk=∑′i=1k1cikTi-1x,  1≤k≤n  
where Tix is the ith Chebyshev polynomial of the first kind, and ∑′ denotes that the first coefficient, c1k, is halved.
2:     ifail – int64int32nag_int scalar
ifail=0 unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:
   ifail=1
On entry,n<1,
orx0≥x1,
ork1<2,
orkp<k1-1,
orldc<k1.
   ifail=2
On entry,lw<2×n×kp+1×n×k1+1+7×n×k1,
orliw<n×k1+2 (i.e., insufficient workspace).
   ifail=3
Either the boundary conditions are not linearly independent (that is, in bc the variable j is set to the same value k for two different values of ii), or the rank of the matrix of equations for the coefficients is less than the number of unknowns. Increasing kp may overcome this latter problem.
   ifail=4
The least squares function nag_linsys_real_gen_lsqsol (f04am) has failed to correct the first approximate solution (see nag_linsys_real_gen_lsqsol (f04am)).
   ifail=-99
An unexpected error has been triggered by this routine. Please contact NAG.
   ifail=-399
Your licence key may have expired or may not have been installed correctly.
   ifail=-999
Dynamic memory allocation failed.

Accuracy

The Chebyshev coefficients are determined by a stable numerical method. The accuracy of the approximate solution may be checked by varying the degree of the polynomials and the number of collocation points (see Further Comments).

Further Comments

The time taken by nag_ode_bvp_coll_sys (d02jb) depends on the size and complexity of the differential system, the degree of the polynomial solution, and the number of matching points.
The collocation points in the interval x0,x1 are chosen to be the extrema of the appropriate shifted Chebyshev polynomial. If kp=k1-1, then the least squares solution reduces to the solution of a system of linear equations, and true collocation results.
The accuracy of the solution may be checked by repeating the calculation with different values of k1 and with kp fixed but kp≫k1-1. If the Chebyshev coefficients decrease rapidly for each component (and consistently for various k1 and kp), the size of the last two or three gives an indication of the error. If the Chebyshev coefficients do not decay rapidly, it is likely that the solution cannot be well-represented by Chebyshev series. Note that the Chebyshev coefficients are calculated for the interval -1,1.
Linear systems of high-order equations in their original form, singular problems, and, indirectly, nonlinear problems can be solved using nag_ode_bvp_coll_nth_comp (d02tg).

Example

This example solves the equation
y′′ + y = 1  
with boundary conditions
y-1 = y1 = 0 .  
The equation is written as the first-order system
y1′ y2′ = 0 1 -1 0 y1 y2 + 0 1  
for solution by nag_ode_bvp_coll_sys (d02jb) and the boundary conditions are written
y1- 1=y11=0.  
We use k1=4, 6 and 8, and kp=10 and 15, so that the different Chebyshev series may be compared. The solution for k1=8 and kp=15 is evaluated by nag_fit_1dcheb_eval2 (e02ak) at nine equally spaced points over the interval -1,1.

Open in the MATLAB editor: d02jb_example

function d02jb_example


fprintf('d02jb example results\n\n');

% Set up initial values.
n     = int64(2);
k1max = 8;
kpmax = 15;
x0    = -1.0;
x1    = 1.0;
c     = zeros(k1max, n);

fprintf('  KP   K1   Chebyshev coefficients\n');
for kp = int64(10:5:kpmax)
  for k1 = int64(4:2:k1max)
    [c, ifail] = d02jb(...
                        n, @cf, @bc, x0, x1, k1, kp);
    % Output results.
    fprintf('%4d ',kp, k1);
    for jord = 1:n
      for kind = 1:k1
        fprintf('%7.4f ',c(kind,jord));
        if mod(kind, 8) == 0 && kind ~= k1
          fprintf('\n          ');
        end
      end
      fprintf('\n          ');
    end
    fprintf('\n');
  end
end
% Now prepare to evaluate and plot the last solution.
fprintf('\n');
k1   = 8;
k1m1 = int64(k1-1);
m    = 9;
ia1  = int64(1);
x    = zeros(m, 1);
y    = zeros(m, n+1);

fprintf(['Last computed solution evaluated at %1d equally spaced ', ...
    'points\n\n'], m);
fprintf('    X       Y(1)      Y(2)\n');
for i = 1:m
  x(i) = (x0*(m-i) + x1*(i-1))/(m-1);
  fprintf('%8.4f  ', x(i));

  for jord = 1:n
    % Calling e02ak to evaluate the polynomial from its Chebyshev
    % representation.
    [y(i, jord), ifail] = e02ak(...
                                 k1m1, x0, x1, c(:,jord), ia1, x(i));
    fprintf('%8.4f  ',y(i, jord));
  end
  fprintf('\n');

  % Calculate the absolute error at this point.
  y(i,n+1) = abs(y(i,1) - 1 + cos(x(i))/cos(1));
end
% Plot results.
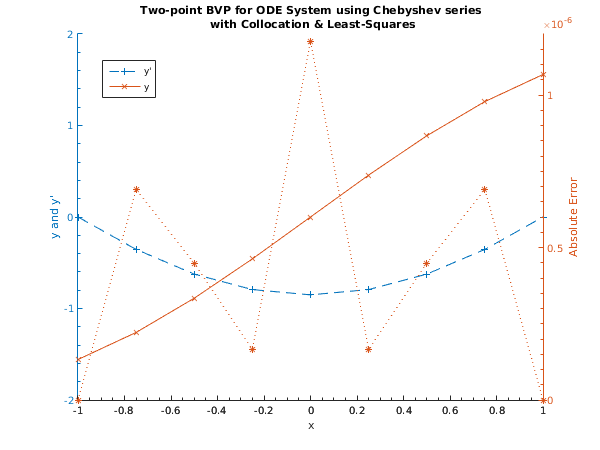
fig1 = figure;
display_plot(x, y, fig1);


function [j, rhs] = bc(i)
  % Define the boundary conditions.
  rhs = 0;
  if (i == 1)
    j = int64(1);
  else
    j = int64(-1);
  end

function result = cf(ii, jj, x)
  % Define the differential equation to be solved.
  if (jj == ii)
    result = 0;
  elseif (ii == 1 && jj == 2)
    result = 1;
  elseif (ii == 2 && jj == 1)
    result = -1;
  elseif (ii == 1)
    result = 0;
  else
    result = 1;
  end

function display_plot(x, y, fig1)
  axes1 = axes('Parent',fig1,'YMinorTick','on','YTick',[-2 -1 0 1 2],...
               'YColor',[0 0.447 0.741],...
               'XMinorTick','on');
  hold(axes1,'on');
  ylabel('y and y''');
  xlabel('x');
  title({'Two-point BVP for ODE System using Chebyshev series',...
         ' with Collocation & Least-Squares'});

  % Create multiple lines using matrix input to plot
  plot1 = plot(x,y(:,1:2),'Parent',axes1);
  set(plot1(1),'DisplayName','y''','Marker','+','LineStyle','--');
  set(plot1(2),'DisplayName','y','Marker','x');
  
  % Create axes
  axes2 = axes('Parent',fig1,'HitTest','off','Color','none',...
               'YMinorTick','on',...
               'YTick',[0 5e-07 1e-06 1.5e-06 2e-06],...
               'YColor',[0.85 0.325 0.098],...
               'YAxisLocation','right',...
               'Position',[0.13 0.11 0.775 0.815]);
  hold(axes2,'on');
  ylabel('Absolute Error');

  plot(x,y(:,3),'Parent',axes2,'DisplayName','y error','Marker','*',...
       'LineStyle',':','Color',[0.85 0.325 0.098]);

  legend1 = legend(axes1,'show');
  set(legend1,'Position',[0.17 0.77 0.09 0.11]);

d02jb example results

  KP   K1   Chebyshev coefficients
  10    4 -0.7798  0.0000  0.3899 -0.0000 
           0.0000  1.5751  0.0000 -0.0629 
          
  10    6 -0.8326 -0.0000  0.4253  0.0000 -0.0090 -0.0000 
          -0.0000  1.6290  0.0000 -0.0724 -0.0000  0.0009 
          
  10    8 -0.8325 -0.0000  0.4253  0.0000 -0.0092 -0.0000  0.0001  0.0000 
          -0.0000  1.6289  0.0000 -0.0724 -0.0000  0.0009  0.0000 -0.0000 
          
  15    4 -0.7829  0.0000  0.3914 -0.0000 
           0.0000  1.5778  0.0000 -0.0631 
          
  15    6 -0.8326 -0.0000  0.4253  0.0000 -0.0090  0.0000 
           0.0000  1.6290  0.0000 -0.0724 -0.0000  0.0009 
          
  15    8 -0.8325 -0.0000  0.4253  0.0000 -0.0092  0.0000  0.0001 -0.0000 
           0.0000  1.6289  0.0000 -0.0724 -0.0000  0.0009  0.0000 -0.0000 
          

Last computed solution evaluated at 9 equally spaced points

    X       Y(1)      Y(2)
 -1.0000    0.0000   -1.5574  
 -0.7500   -0.3542   -1.2616  
 -0.5000   -0.6242   -0.8873  
 -0.2500   -0.7933   -0.4579  
  0.0000   -0.8508    0.0000  
  0.2500   -0.7933    0.4579  
  0.5000   -0.6242    0.8873  
  0.7500   -0.3542    1.2616  
  1.0000    0.0000    1.5574
d02jb_fig1.png
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015