NAG Toolbox: nag_ode_bvp_fd_nonlin_fixedbc (d02ga)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{u}\left(\mathbf{n},2\right)$ – double array

$\mathbf{u}\left(\mathit{i},1\right)$ must be set to the known or estimated value of $y_{\mathit{i}}$ at $a$ and $\mathbf{u}\left(\mathit{i},2\right)$ must be set to the known or estimated value of $y_{\mathit{i}}$ at $b$, for $\mathit{i}=1,2,\dots ,\mathit{n}$.

2:     $\mathrm{v}\left(\mathbf{n},2\right)$ – double array

$\mathbf{v}\left(\mathit{i},\mathit{j}\right)$ must be set to $0.0$ if $\mathbf{u}\left(\mathit{i},\mathit{j}\right)$ is a known value and to $1.0$ if $\mathbf{u}\left(\mathit{i},\mathit{j}\right)$ is an estimated value, for $\mathit{i}=1,2,\dots ,\mathit{n}$ and $\mathit{j}=1,2$.

Constraint: precisely $\mathit{n}$ of the $\mathbf{v}\left(i,j\right)$ must be set to $0.0$, i.e., precisely $\mathit{n}$ of the $\mathbf{u}\left(i,j\right)$ must be known values, and these must not be all at $a$ or all at $b$.

3:     $\mathrm{a}$ – double scalar

$a$, the left-hand boundary point.

4:     $\mathrm{b}$ – double scalar

$b$, the right-hand boundary point.

Constraint: $\mathbf{b}>\mathbf{a}$.

5:     $\mathrm{tol}$ – double scalar

A positive absolute error tolerance. If

$$a=x_1<x_2<\cdots <x_{\mathbf{np}}=b$$

is the final mesh, $z_j\left(x_i\right)$ is the $j$th component of the approximate solution at $x_i$, and $y_j\left(x\right)$ is the $j$th component of the true solution of equation (1) (see Description) and the boundary conditions, then, except in extreme cases, it is expected that

$$\left|z_j\left(x_i\right)-y_j\left(x_i\right)\right|\le \mathbf{tol}\text{, \hspace{1em}}i=1,2,\dots ,\mathbf{np}\text{ and }j=1,2,\dots ,\mathit{n}\text{.}$$

(2)

Constraint: $\mathbf{tol}>0.0$.

6:     $\mathrm{fcn}$ – function handle or string containing name of m-file

fcn must evaluate the functions $f_{\mathit{i}}$ (i.e., the derivatives $y_{\mathit{i}}^{\prime }$), for $\mathit{i}=1,2,\dots ,\mathit{n}$, at a general point $x$.

[f] = fcn(x, y)

Input Parameters

1:     $\mathrm{x}$ – double scalar

$x$, the value of the argument.

2:     $\mathrm{y}\left(:\right)$ – double array

$y_{\mathit{i}}$, for $\mathit{i}=1,2,\dots ,\mathit{n}$, the value of the argument.

Output Parameters

1:     $\mathrm{f}\left(:\right)$ – double array

The values of $f_{\mathit{i}}$, for $\mathit{i}=1,2,\dots ,\mathit{n}$.

7:     $\mathrm{x}\left(\mathbf{mnp}\right)$ – double array

If $\mathbf{np}\ge 4$ (see np), the first np elements must define an initial mesh. Otherwise the elements of x need not be set.

Constraint:

$$\mathbf{a}=\mathbf{x}\left(1\right)<\mathbf{x}\left(2\right)<\cdots <\mathbf{x}\left(\mathbf{np}\right)=\mathbf{b}\text{, \hspace{1em}}\mathbf{np}\ge 4\text{.}$$

(3)

8:     $\mathrm{np}$ – int64int32nag_int scalar

Determines whether a default or user-supplied mesh is used.

$\mathbf{np}=0$

A default value of $4$ for np and a corresponding equispaced mesh $\mathbf{x}\left(1\right),\mathbf{x}\left(2\right),\dots ,\mathbf{x}\left(\mathbf{np}\right)$ are used.

$\mathbf{np}\ge 4$

You must define an initial mesh using the array x as described.

Constraint: $\mathbf{np}=0$ or $4\le \mathbf{np}\le \mathbf{mnp}$.

Optional Input Parameters

1:     $\mathrm{n}$ – int64int32nag_int scalar

Default: the first dimension of the arrays u, v. (An error is raised if these dimensions are not equal.)

$\mathit{n}$, the number of equations.

Constraint: $\mathbf{n}\ge 2$.

2:     $\mathrm{mnp}$ – int64int32nag_int scalar

Default: the dimension of the array x.

The maximum permitted number of mesh points.

Constraint: $\mathbf{mnp}\ge 32$.

Output Parameters

1:     $\mathrm{x}\left(\mathbf{mnp}\right)$ – double array

$\mathbf{x}\left(1\right),\mathbf{x}\left(2\right),\dots ,\mathbf{x}\left(\mathbf{np}\right)$ define the final mesh (with the returned value of np) satisfying the relation (3).

2:     $\mathrm{y}\left(\mathbf{n},\mathbf{mnp}\right)$ – double array

The approximate solution $z_j\left(x_i\right)$ satisfying (2), on the final mesh, that is

$$\mathbf{y}\left(j,i\right)=z_j\left(x_i\right)\text{, \hspace{1em}}i=1,2,\dots ,\mathbf{np}\text{ and }j=1,2,\dots ,\mathit{n}\text{,}$$

where np is the number of points in the final mesh.

The remaining columns of y are not used.

3:     $\mathrm{np}$ – int64int32nag_int scalar

The number of points in the final (returned) mesh.

4:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

   $\mathbf{ifail}=1$

One or more of the arguments n, tol, np, mnp, lw or liw has been incorrectly set, or $\mathbf{b}\le \mathbf{a}$, or the condition (3) on x is not satisfied, or the number of known boundary values (specified by v) is not n.

   $\mathbf{ifail}=2$

The Newton iteration has failed to converge. This could be due to there being too few points in the initial mesh or to the initial approximate solution being too inaccurate. If this latter reason is suspected you should use nag_ode_bvp_fd_nonlin_gen (d02ra) instead. If the warning ‘Jacobian matrix is singular’ is printed this could be due to specifying zero estimated boundary values and these should be varied. This warning could also be printed in the unlikely event of the Jacobian matrix being calculated inaccurately. If you cannot make changes to prevent the warning then nag_ode_bvp_fd_nonlin_gen (d02ra) should be used.

W  $\mathbf{ifail}=3$

The Newton iteration has reached round-off level. It could be, however, that the answer returned is satisfactory. This error might occur if too much accuracy is requested.

W  $\mathbf{ifail}=4$

A finer mesh is required for the accuracy requested; that is mnp is not large enough.

   $\mathbf{ifail}=5$

A serious error has occurred in a call to nag_ode_bvp_fd_nonlin_fixedbc (d02ga). Check all array subscripts and function argument lists in calls to nag_ode_bvp_fd_nonlin_fixedbc (d02ga). Seek expert help.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: d02ga_example

function d02ga_example


fprintf('d02ga example results\n\n');

% For communication with fcn & display_plot.
global beta;

% Initialize variables and arrays.
u = [0, 10; 0, 1; 0, 0];
v = [0, 1; 0, 0; 1, 1];
a = 0;
b = 10;
tol = 0.001;
x = zeros(40, 1);
np = int64(26);
beta = double(0);
n = 3;
for i = 2:np-1
    x(i) = (double(np-i)*a+double(i-1)*b)/double(np-1);
end
x(np) = b;

for k = 1:2

  [xOut, y, npOut, ifail] = ...
    d02ga(...
           u, v, a, b, tol, @fcn, x, np);

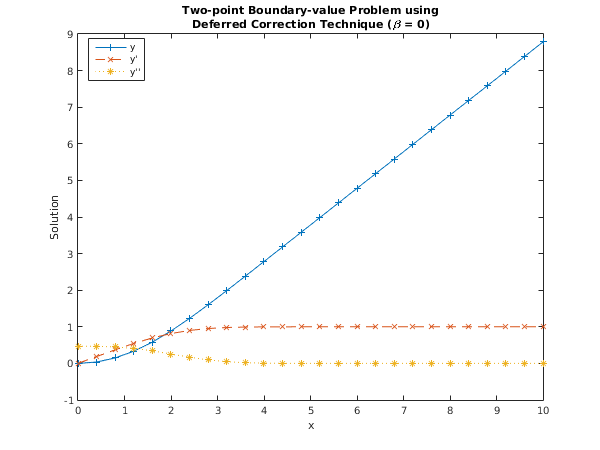
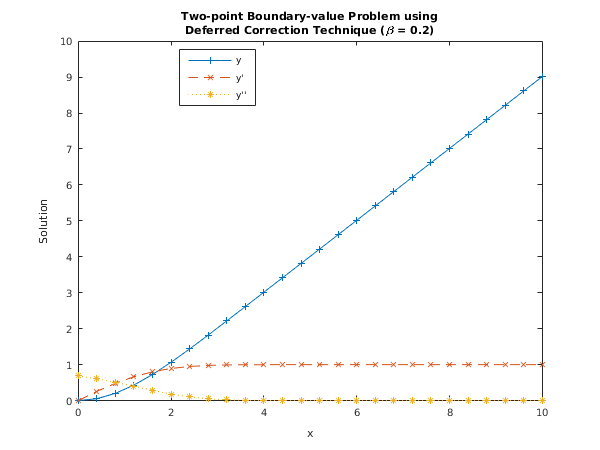
  fprintf('Problem with beta = %1.2f \n\n',beta);
  fprintf('Solution on final mesh of %1.0f points\n\n',npOut);
  disp('  x         y_1           y_2           y_3');
  for i = 1:npOut;
    fprintf('%6.3f     %8.5f      %8.5f      %8.5f\n', x(i),y(1:3,i));
  end

  % Plot results.
  xplot = x(1:npOut);
  yplot = y(:,1:npOut); 
  if k == 1
    fig1 = figure;
    display_plot(xplot, yplot);
  else
    fig2 = figure;
    display_plot(xplot, yplot);
  end
  disp(' ');
  beta = double(beta + 0.2);
end



function f = fcn(x,y)
  % For communication with the main routine.
  global beta;

  % Evaluate the derivatives.
  f = zeros(3,1);
  f(1) = y(2);
  f(2) = y(3);
  f(3) = -y(1)*y(3)- beta*(1.0-y(2)*y(2));

function display_plot(x, y)
  % For communication with the main routine.
  global beta;
  % Plot the three curves.
  plot(x, y(1,:), '-+', ...
       x, y(2,:), '--x', ...
       x, y(3,:), ':*');
  % Add title.
  title({['Two-point Boundary-value Problem using'],...
         ['Deferred Correction Technique (\beta = ',num2str(beta),')']});
  % Label the axes.
  xlabel('x');
  ylabel('Solution');
  % Add legend.
  legend('y','y''','y''''','Location','Best');

d02ga example results

Problem with beta = 0.00 

Solution on final mesh of 26 points

  x         y_1           y_2           y_3
 0.000      0.00000       0.00000       0.46948
 0.400      0.03754       0.18762       0.46725
 0.800      0.14970       0.37191       0.45109
 1.200      0.33363       0.54504       0.41042
 1.600      0.58277       0.69635       0.34245
 2.000      0.88639       0.81635       0.25584
 2.400      1.23094       0.90088       0.16781
 2.800      1.60263       0.95288       0.09525
 3.200      1.98997       0.98045       0.04636
 3.600      2.38505       0.99296       0.01928
 4.000      2.78340       0.99780       0.00686
 4.400      3.18292       0.99940       0.00210
 4.800      3.58279       0.99986       0.00055
 5.200      3.98276       0.99997       0.00012
 5.600      4.38276       1.00000       0.00002
 6.000      4.78276       1.00000       0.00000
 6.400      5.18276       1.00000       0.00000
 6.800      5.58276       1.00000       0.00000
 7.200      5.98276       1.00000      -0.00000
 7.600      6.38276       1.00000       0.00000
 8.000      6.78276       1.00000      -0.00000
 8.400      7.18276       1.00000       0.00000
 8.800      7.58276       1.00000      -0.00000
 9.200      7.98276       1.00000       0.00000
 9.600      8.38276       1.00000      -0.00000
10.000      8.78276       1.00000      -0.00000
 
Problem with beta = 0.20 

Solution on final mesh of 26 points

  x         y_1           y_2           y_3
 0.000      0.00000       0.00000       0.68654
 0.400      0.05279       0.25843       0.60395
 0.800      0.20203       0.48144       0.50912
 1.200      0.43245       0.66359       0.40014
 1.600      0.72676       0.80075       0.28602
 2.000      1.06701       0.89385       0.18212
 2.400      1.43680       0.94979       0.10167
 2.800      1.82330       0.97911       0.04923
 3.200      2.21802       0.99240       0.02056
 3.600      2.61623       0.99759       0.00740
 4.000      3.01569       0.99933       0.00230
 4.400      3.41555       0.99984       0.00062
 4.800      3.81552       0.99997       0.00014
 5.200      4.21551       0.99999       0.00003
 5.600      4.61551       1.00000       0.00000
 6.000      5.01551       1.00000       0.00000
 6.400      5.41551       1.00000      -0.00000
 6.800      5.81551       1.00000      -0.00000
 7.200      6.21551       1.00000      -0.00000
 7.600      6.61551       1.00000      -0.00000
 8.000      7.01551       1.00000      -0.00000
 8.400      7.41551       1.00000      -0.00000
 8.800      7.81551       1.00000      -0.00000
 9.200      8.21551       1.00000      -0.00000
 9.600      8.61551       1.00000      -0.00000
10.000      9.01551       1.00000      -0.00000