NAG Toolbox: nag_ode_bvp_fd_nonlin_gen (d02ra)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{np}$ – int64int32nag_int scalar

Must be set to the number of points to be used in the initial mesh.

Constraint: $4\le \mathbf{np}\le \mathbf{mnp}$.

2:     $\mathrm{numbeg}$ – int64int32nag_int scalar

The number of left-hand boundary conditions (that is the number involving $y\left(a\right)$ only).

Constraint: $0\le \mathbf{numbeg}<\mathbf{n}$.

3:     $\mathrm{nummix}$ – int64int32nag_int scalar

The number of coupled boundary conditions (that is the number involving both $y\left(a\right)$ and $y\left(b\right)$).

Constraint: $0\le \mathbf{nummix}\le \mathbf{n}-\mathbf{numbeg}$.

4:     $\mathrm{tol}$ – double scalar

A positive absolute error tolerance. If

$$a=x_1<x_2<\cdots <x_{\mathbf{np}}=b$$

is the final mesh, $z_j\left(x_i\right)$ is the $j$th component of the approximate solution at $x_i$, and $y_j\left(x\right)$ is the $j$th component of the true solution of (1) and (2), then, except in extreme circumstances, it is expected that

$$\left|z_j\left(x_i\right)-y_j\left(x_i\right)\right|\le \mathbf{tol}\text{, \hspace{1em}}i=1,2,\dots ,\mathbf{np}\text{ and }j=1,2,\dots ,n\text{.}$$

(5)

Constraint: $\mathbf{tol}>0.0$.

5:     $\mathrm{init}$ – int64int32nag_int scalar

Indicates whether you wish to supply an initial mesh and approximate solution ($\mathbf{init}=1$) or whether default values are to be used, ($\mathbf{init}=0$).

Constraint: $\mathbf{init}=0$ or $1$.

6:     $\mathrm{x}\left(\mathbf{mnp}\right)$ – double array

You must set $\mathbf{x}\left(1\right)=a$ and $\mathbf{x}\left(\mathbf{np}\right)=b$. If $\mathbf{init}=0$ on entry a default equispaced mesh will be used, otherwise you must specify a mesh by setting $\mathbf{x}\left(\mathit{i}\right)=x_{\mathit{i}}$, for $\mathit{i}=2,3,\dots ,\mathbf{np}-1$.

Constraints:

• if $\mathbf{init}=0$, $\mathbf{x}\left(1\right)<\mathbf{x}\left(\mathbf{np}\right)$;
• if $\mathbf{init}=1$, $\mathbf{x}\left(1\right)<\mathbf{x}\left(2\right)<\cdots <\mathbf{x}\left(\mathbf{np}\right)$.

7:     $\mathrm{y}\left(\mathit{ldy},\mathbf{mnp}\right)$ – double array

ldy, the first dimension of the array, must satisfy the constraint $\mathit{ldy}\ge \mathbf{n}$.

If $\mathbf{init}=0$, then y need not be set.

If $\mathbf{init}=1$, then the array y must contain an initial approximation to the solution such that $\mathbf{y}\left(j,i\right)$ contains an approximation to

$$y_j\left(x_i\right)\text{, \hspace{1em}}i=1,2,\dots ,\mathbf{np}\text{ and }j=1,2,\dots ,n\text{.}$$

8:     $\mathrm{fcn}$ – function handle or string containing name of m-file

fcn must evaluate the functions $f_i$ (i.e., the derivatives $y_i^{\prime }$) at a general point $x$ for a given value of $\epsilon$, the continuation parameter (see Description).

[f] = fcn(x, eps, y, n)

Input Parameters

1:     $\mathrm{x}$ – double scalar

$x$, the value of the independent variable.

2:     $\mathrm{eps}$ – double scalar

$\epsilon$, the value of the continuation parameter. This is $1$ if continuation is not being used.

3:     $\mathrm{y}\left(\mathbf{n}\right)$ – double array

$y_{\mathit{i}}$, for $\mathit{i}=1,2,\dots ,\mathit{n}$, the values of the dependent variables at $x$.

4:     $\mathrm{n}$ – int64int32nag_int scalar

$n$, the number of equations.

Output Parameters

1:     $\mathrm{f}\left(\mathbf{n}\right)$ – double array

The values of the derivatives $f_{\mathit{i}}$ evaluated at $x$ given $\epsilon$, for $\mathit{i}=1,2,\dots ,\mathit{n}$.

9:     $\mathrm{g}$ – function handle or string containing name of m-file

g must evaluate the boundary conditions in equation (3) and place them in the array bc.

[bc] = g(eps, ya, yb, n)

Input Parameters

1:     $\mathrm{eps}$ – double scalar

$\epsilon$, the value of the continuation parameter. This is $1$ if continuation is not being used.

2:     $\mathrm{ya}\left(\mathbf{n}\right)$ – double array

The value $y_{\mathit{i}}\left(a\right)$, for $\mathit{i}=1,2,\dots ,n$.

3:     $\mathrm{yb}\left(\mathbf{n}\right)$ – double array

The value $y_{\mathit{i}}\left(b\right)$, for $\mathit{i}=1,2,\dots ,n$.

4:     $\mathrm{n}$ – int64int32nag_int scalar

$\mathit{n}$, the number of equations.

Output Parameters

1:     $\mathrm{bc}\left(\mathbf{n}\right)$ – double array

The values $g_{\mathit{i}}\left(y\left(a\right),y\left(b\right),\epsilon \right)$, for $\mathit{i}=1,2,\dots ,n$. These must be ordered as follows:

(i)	first, the conditions involving only $y\left(a\right)$ (see numbeg);
(ii)	next, the nummix coupled conditions involving both $y\left(a\right)$ and $y\left(b\right)$ (see nummix); and,
(iii)	finally, the conditions involving only $y\left(b\right)$ ($\mathbf{n}-\mathbf{numbeg}-\mathbf{nummix}$).

10:   $\mathrm{ijac}$ – int64int32nag_int scalar

Indicates whether or not you are supplying Jacobian evaluation functions.

$\mathbf{ijac}\ne 0$

You must supply jacobf and jacobg and also, when continuation is used, jaceps and jacgep.

$\mathbf{ijac}=0$

Numerical differentiation is used to calculate the Jacobian and the functions nag_ode_bvp_fd_nonlin_gen_dummy_jacobf (d02gaw), nag_ode_bvp_fd_nonlin_gen_dummy_jacobg (d02gax), nag_ode_bvp_fd_nonlin_gen_dummy_jaceps (d02gay) and nag_ode_bvp_fd_nonlin_gen_dummy_jacgep (d02gaz) respectively may be used as the dummy arguments.

11:   $\mathrm{jacobf}$ – function handle or string containing name of m-file

jacobf evaluates the Jacobian $\left(\frac{\partial f_{\mathit{i}}}{\partial y_{\mathit{j}}}\right)$, for $\mathit{i}=1,2,\dots ,n$ and $\mathit{j}=1,2,\dots ,n$, given $x$ and $y_{\mathit{j}}$, for $\mathit{j}=1,2,\dots ,n$.

If all Jacobians are to be approximated internally by numerical differentiation then it must be replaced by the NAG defined null function pointer NULLFN.

If $\mathbf{ijac}=0$, then numerical differentiation is used to calculate the Jacobian and the function nag_ode_bvp_fd_nonlin_gen_dummy_jacgep (d02gaz) may be substituted for this argument.

[f] = jacobf(x, eps, y, n)

Input Parameters

1:     $\mathrm{x}$ – double scalar

$x$, the value of the independent variable.

2:     $\mathrm{eps}$ – double scalar

$\epsilon$, the value of the continuation parameter. This is $1$ if continuation is not being used.

3:     $\mathrm{y}\left(\mathbf{n}\right)$ – double array

$y_{\mathit{i}}$, for $\mathit{i}=1,2,\dots ,\mathit{n}$, the values of the dependent variables at $x$.

4:     $\mathrm{n}$ – int64int32nag_int scalar

$\mathit{n}$, the number of equations.

Output Parameters

1:     $\mathrm{f}\left(\mathbf{n},\mathbf{n}\right)$ – double array

$\mathbf{f}\left(\mathit{j},\mathit{i}\right)$ must be set to the value of $\frac{\partial f_{\mathit{i}}}{\partial y_{\mathit{j}}}$, evaluated at the point $\left(x,y\right)$, for $\mathit{i}=1,2,\dots ,n$ and $\mathit{j}=1,2,\dots ,n$.

12:   $\mathrm{jacobg}$ – function handle or string containing name of m-file

jacobg evaluates the Jacobians $\left(\frac{\partial g_i}{\partial y_j\left(a\right)}\right)$ and $\left(\frac{\partial g_i}{\partial y_j\left(b\right)}\right)$. The ordering of the rows of aj and bj must correspond to the ordering of the boundary conditions described in the specification of g.

If all Jacobians are to be approximated internally by numerical differentiation then it must be replaced by the NAG defined null function pointer NULLFN.

If $\mathbf{ijac}=0$, then numerical differentiation is used to calculate the Jacobian and the function nag_ode_bvp_fd_nonlin_gen_dummy_jaceps (d02gay) may be substituted for this argument.

[aj, bj] = jacobg(eps, ya, yb, n)

Input Parameters

1:     $\mathrm{eps}$ – double scalar

$\epsilon$, the value of the continuation parameter. This is $1$ if continuation is not being used.

2:     $\mathrm{ya}\left(\mathbf{n}\right)$ – double array

The value $y_{\mathit{i}}\left(a\right)$, for $\mathit{i}=1,2,\dots ,n$.

3:     $\mathrm{yb}\left(\mathbf{n}\right)$ – double array

The value $y_{\mathit{i}}\left(b\right)$, for $\mathit{i}=1,2,\dots ,n$.

4:     $\mathrm{n}$ – int64int32nag_int scalar

$\mathit{n}$, the number of equations.

Output Parameters

1:     $\mathrm{aj}\left(\mathbf{n},\mathbf{n}\right)$ – double array

$\mathbf{aj}\left(\mathit{i},\mathit{j}\right)$ must be set to the value $\frac{\partial g_{\mathit{i}}}{\partial y_{\mathit{j}}\left(a\right)}$, for $\mathit{i}=1,2,\dots ,n$ and $\mathit{j}=1,2,\dots ,n$.

2:     $\mathrm{bj}\left(\mathbf{n},\mathbf{n}\right)$ – double array

$\mathbf{bj}\left(\mathit{i},\mathit{j}\right)$ must be set to the value $\frac{\partial g_{\mathit{i}}}{\partial y_{\mathit{j}}\left(b\right)}$, for $\mathit{i}=1,2,\dots ,n$ and $\mathit{j}=1,2,\dots ,n$.

13:   $\mathrm{deleps}$ – double scalar

Must be given a value which specifies whether continuation is required. If $\mathbf{deleps}\le 0.0$ or $\mathbf{deleps}\ge 1.0$ then it is assumed that continuation is not required. If $0.0<\mathbf{deleps}<1.0$ then it is assumed that continuation is required unless $\mathbf{deleps}<\sqrt{\mathit{machine precision}}$ when an error exit is taken. deleps is used as the increment ${\epsilon }_2-{\epsilon }_1$ (see (4)) and the choice $\mathbf{deleps}=0.1$ is recommended.

14:   $\mathrm{jaceps}$ – function handle or string containing name of m-file

jaceps evaluates the derivative $\frac{\partial f_i}{\partial \epsilon }$ given $x$ and $y$ if continuation is being used.

If all Jacobians (derivatives) are to be approximated internally by numerical differentiation, or continuation is not being used, then it must be replaced by the NAG defined null function pointer NULLFN.

If $\mathbf{ijac}=0$, then numerical differentiation is used to calculate the Jacobian and the function nag_ode_bvp_fd_nonlin_gen_dummy_jacobf (d02gaw) may be substituted for this argument.

[f] = jaceps(x, eps, y, n)

Input Parameters

1:     $\mathrm{x}$ – double scalar

$x$, the value of the independent variable.

2:     $\mathrm{eps}$ – double scalar

$\epsilon$, the value of the continuation parameter.

3:     $\mathrm{y}\left(\mathbf{n}\right)$ – double array

The solution values $y_{\mathit{i}}$, for $\mathit{i}=1,2,\dots ,n$, at the point $x$.

4:     $\mathrm{n}$ – int64int32nag_int scalar

$\mathit{n}$, the number of equations.

Output Parameters

1:     $\mathrm{f}\left(\mathbf{n}\right)$ – double array

$\mathbf{f}\left(\mathit{i}\right)$ must contain the value $\frac{\partial f_{\mathit{i}}}{\partial \epsilon }$ at the point $\left(x,y\right)$, for $\mathit{i}=1,2,\dots ,n$.

15:   $\mathrm{jacgep}$ – function handle or string containing name of m-file

jacgep evaluates the derivatives $\frac{\partial g_i}{\partial \epsilon }$ if continuation is being used.

If all Jacobians (derivatives) are to be approximated internally by numerical differentiation, or continuation is not being used, then it must be replaced by the NAG defined null function pointer NULLFN.

If $\mathbf{ijac}=0$, then numerical differentiation is used to calculate the Jacobian and the function nag_ode_bvp_fd_nonlin_gen_dummy_jacobg (d02gax) may be substituted for this argument.

[bcep] = jacgep(eps, ya, yb, n)

Input Parameters

1:     $\mathrm{eps}$ – double scalar

$\epsilon$, the value of the continuation parameter.

2:     $\mathrm{ya}\left(\mathbf{n}\right)$ – double array

The value of $y_{\mathit{i}}\left(a\right)$, for $\mathit{i}=1,2,\dots ,n$.

3:     $\mathrm{yb}\left(\mathbf{n}\right)$ – double array

The value of $y_{\mathit{i}}\left(b\right)$, for $\mathit{i}=1,2,\dots ,n$.

4:     $\mathrm{n}$ – int64int32nag_int scalar

$\mathit{n}$, the number of equations.

Output Parameters

1:     $\mathrm{bcep}\left(\mathbf{n}\right)$ – double array

$\mathbf{bcep}\left(\mathit{i}\right)$ must contain the value of $\frac{\partial g_{\mathit{i}}}{\partial \epsilon }$, for $\mathit{i}=1,2,\dots ,n$.

Optional Input Parameters

1:     $\mathrm{n}$ – int64int32nag_int scalar

Default: the first dimension of the array y.

$\mathit{n}$, the number of differential equations.

Constraint: $\mathbf{n}>0$.

2:     $\mathrm{mnp}$ – int64int32nag_int scalar

Default: the dimension of the array x and the second dimension of the array y. (An error is raised if these dimensions are not equal.)

mnp must be set to the maximum permitted number of points in the finite difference mesh. If lwork or liwork are too small then internally mnp will be replaced by the maximum permitted by these values. (A warning message will be output if on entry ifail is set to obtain monitoring information.)

Constraint: $\mathbf{mnp}\ge 32$.

Output Parameters

1:     $\mathrm{np}$ – int64int32nag_int scalar

The number of points in the final mesh.

2:     $\mathrm{x}\left(\mathbf{mnp}\right)$ – double array

$\mathbf{x}\left(1\right),\mathbf{x}\left(2\right),\dots ,\mathbf{x}\left(\mathbf{np}\right)$ define the final mesh (with the returned value of np) and $\mathbf{x}\left(1\right)=a$ and $\mathbf{x}\left(\mathbf{np}\right)=b$.

3:     $\mathrm{y}\left(\mathit{ldy},\mathbf{mnp}\right)$ – double array

The approximate solution $z_j\left(x_i\right)$ satisfying (5) on the final mesh, that is

$$\mathbf{y}\left(j,i\right)=z_j\left(x_i\right)\text{, \hspace{1em}}i=1,2,\dots ,\mathbf{np}\text{ and }j=1,2,\dots ,n\text{,}$$

where np is the number of points in the final mesh. If an error has occurred then y contains the latest approximation to the solution. The remaining columns of y are not used.

4:     $\mathrm{abt}\left(\mathbf{n}\right)$ – double array

$\mathbf{abt}\left(\mathit{i}\right)$, for $\mathit{i}=1,2,\dots ,n$, holds the largest estimated error (in magnitude) of the $i$th component of the solution over all mesh points.

5:     $\mathrm{deleps}$ – double scalar

An overestimate of the increment ${\epsilon }_p-{\epsilon }_{p-1}$ (in fact the value of the increment which would have been tried if the restriction ${\epsilon }_p=1$ had not been imposed). If continuation was not requested then $\mathbf{deleps}=0.0$.

If continuation is not requested then jaceps and jacgep may each be replaced by dummy actual arguments in the call to nag_ode_bvp_fd_nonlin_gen (d02ra). (nag_ode_bvp_fd_nonlin_gen_dummy_jacobf (d02gaw) and nag_ode_bvp_fd_nonlin_gen_dummy_jacobg (d02gax) respectively may be used as the dummy arguments.)

6:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

   $\mathbf{ifail}=1$

One or more of the arguments n, mnp, np, numbeg, nummix, tol, deleps, lwork or liwork is incorrectly set, or $\mathbf{x}\left(1\right)\ge \mathbf{x}\left(\mathbf{np}\right)$ or the mesh points $\mathbf{x}\left(i\right)$ are not in strictly ascending order.

   $\mathbf{ifail}=2$

A finer mesh is required for the accuracy requested; that is mnp is not large enough. This error exit normally occurs when the problem being solved is difficult (for example, there is a boundary layer) and high accuracy is requested. A poor initial choice of mesh points will make this error exit more likely.

   $\mathbf{ifail}=3$

The Newton iteration has failed to converge. There are several possible causes for this error:

(i)	faulty coding in one of the Jacobian calculation functions;
(ii)	if $\mathbf{ijac}=0$ then inaccurate Jacobians may have been calculated numerically (this is a very unlikely cause); or,
(iii)	a poor initial mesh or initial approximate solution has been selected either by you or by default or there are not enough points in the initial mesh. Possibly, you should try the continuation facility.

W  $\mathbf{ifail}=4$

The Newton iteration has reached round-off error level. It could be however that the answer returned is satisfactory. The error is likely to occur if too high an accuracy is requested.

   $\mathbf{ifail}=5$

The Jacobian calculated by jacobg (or the equivalent matrix calculated by numerical differentiation) is singular. This may occur due to faulty coding of jacobg or, in some circumstances, to a zero initial choice of approximate solution (such as is chosen when $\mathbf{init}=0$).

   $\mathbf{ifail}=6$

There is no dependence on $\epsilon$ when continuation is being used. This can be due to faulty coding of jaceps or jacgep or, in some circumstances, to a zero initial choice of approximate solution (such as is chosen when $\mathbf{init}=0$).

   $\mathbf{ifail}=7$

deleps is required to be less than machine precision for continuation to proceed. It is likely that either the problem (3) has no solution for some value near the current value of $\epsilon$ (see the advisory print out from nag_ode_bvp_fd_nonlin_gen (d02ra)) or that the problem is so difficult that even with continuation it is unlikely to be solved using this function. If the latter cause is suspected then using more mesh points initially may help.

   $\mathbf{ifail}=8$

   $\mathbf{ifail}=9$

A serious error has occurred in an internal call. Check all array subscripts and function argument lists in calls to nag_ode_bvp_fd_nonlin_gen (d02ra). Seek expert help.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: d02ra_example

function d02ra_example


fprintf('d02ra example results\n\n');

% Initialize variables and arrays.
n      = 3;
np     = int64(17);
mnp    = int64(40);
numbeg = int64(2);
nummix = int64(0);
tol    = 0.0001;
init   = int64(0);
x      = zeros(mnp,1);
x(np)  = 10;
y      = zeros(n,mnp);
ijac   = int64(1);
deleps = 0.1;

% Call NAG routine.
[np, x, y, abt, deleps, ifail] = ...
  d02ra(...
        np, numbeg, nummix, tol, init, x, y, @fcn, @g, ijac, @jacobf, ...
        @jacobg, deleps, @jaceps, @jacgep);

% Output results.
fprintf(['Calculation using analytic Jacobians \n\n'], ...
        ['Solution on final mesh of %4d points\n\n'], np);
fprintf('     x         y_1       y_2      y_3\n');
for j = 1:np
  fprintf('%10.4f',x(j),y(1:n,j));
  fprintf('\n');
end
fprintf('\n   Maximum estimated error by components\n');
fprintf('%12.2e', abt);
fprintf('\n');
% Plot results.
fig1 = figure;
display_plot(x(1:np), y(:,1:np))


function f = fcn(x, eps, y, n)
  % Evaluate derivative vector.
  f = zeros(n,1);
  f(1) = y(2);
  f(2) = y(3);
  f(3) = -y(1)*y(3) - 2*(1-y(2)^2)*eps;

function bc = g(eps, ya, yb, n)
  % Evaluate the boundary conditions.
  bc = zeros(n,1);
  bc(1) = ya(1);
  bc(2) = ya(2);
  bc(3) = yb(2) - 1;

function f = jaceps(x, eps, y, n)
  % Evaluate the derivative w.r.t. eps.
  f = zeros(n,1);
  f(1) = 0;
  f(2) = 0;
  f(3) = -2*(1-y(2)^2);

function bcep = jacgep(eps, ya, yb, n)
  % Evaluate the derivatives of the boundary conditions w.r.t. eps.
  bcep = zeros(n,1);

function f = jacobf(x, eps, y, n)
  % Evaluate the Jacobian.
  f = zeros(n,n);
  f(1,2) = 1;
  f(2,3) = 1;
  f(3,1) = -y(3);
  f(3,2) = 4*y(2)*eps;
  f(3,3) = -y(1);

function [aj, bj] = jacobg(eps, ya, yb, n)
  % Evaluate the Jacobian for the boundary conditions.
  aj = zeros(n,n);
  bj = zeros(n,n);
  aj(1,1) = 1;
  aj(2,2) = 1;
  bj(3,2) = 1;

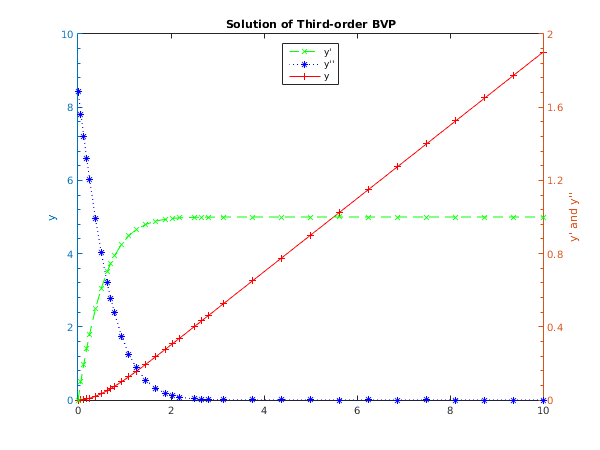
function display_plot(x, y)
  % Plot two of the curves, then add the other one.
  [haxes, hline1, hline2] = plotyy(x, y(1,:), x, y(2,:));
  % We want the third curve to be plotted on the right-hand y-axis.
  axes(haxes(2));
  hold on
  hline3 = plot(x, y(3,:));
  % Set the axis limits and the tick specifications to beautify the plot.
  set(haxes(1), 'YLim', [0 10]);
  set(haxes(1), 'YMinorTick', 'on');
  set(haxes(1), 'YTick', [0:2:10]);
  set(haxes(2), 'YLim', [0 2]);
  set(haxes(2), 'YMinorTick', 'on');
  set(haxes(2), 'YTick', [0:0.4:2]);
  for iaxis = 1:2
    % These properties must be the same for both sets of axes.
    set(haxes(iaxis), 'XLim', [0 10]);
    set(haxes(iaxis), 'XTick', [0:2:10]);
  end
  set(gca, 'box', 'off'); 
  % Add title.
  title('Solution of Third-order BVP');
  % Label the axes.
  xlabel('x');
  ylabel(haxes(1), 'y');
  ylabel(haxes(2), 'y'' and y''''');
  % Add a legend.
  legend('y''','y''''','y','Location','North')
  % Set some features of the three lines.
  set(hline1,'Linewidth',0.25,'Marker','+','LineStyle','-','Color','red');
  set(hline2,'Linewidth',0.25,'Marker','x','LineStyle','--','Color','green');
  set(hline3,'Linewidth',0.25,'Marker','*','LineStyle',':','Color','blue');

d02ra example results

Calculation using analytic Jacobians 

     x         y_1       y_2      y_3
    0.0000    0.0000    0.0000    1.6872
    0.0625    0.0032    0.1016    1.5626
    0.1250    0.0125    0.1954    1.4398
    0.1875    0.0275    0.2816    1.3203
    0.2500    0.0476    0.3605    1.2054
    0.3750    0.1015    0.4976    0.9924
    0.5000    0.1709    0.6097    0.8048
    0.6250    0.2530    0.6999    0.6438
    0.7031    0.3095    0.7467    0.5563
    0.7812    0.3695    0.7871    0.4784
    0.9375    0.4978    0.8513    0.3490
    1.0938    0.6346    0.8977    0.2502
    1.2500    0.7776    0.9308    0.1763
    1.4583    0.9748    0.9598    0.1077
    1.6667    1.1768    0.9773    0.0639
    1.8750    1.3815    0.9876    0.0367
    2.0312    1.5362    0.9922    0.0238
    2.1875    1.6915    0.9952    0.0151
    2.5000    2.0031    0.9983    0.0058
    2.6562    2.1591    0.9990    0.0035
    2.8125    2.3153    0.9994    0.0021
    3.1250    2.6277    0.9998    0.0007
    3.7500    3.2526    1.0000    0.0001
    4.3750    3.8776    1.0000    0.0000
    5.0000    4.5026    1.0000    0.0000
    5.6250    5.1276    1.0000   -0.0000
    6.2500    5.7526    1.0000    0.0000
    6.8750    6.3776    1.0000   -0.0000
    7.5000    7.0026    1.0000    0.0000
    8.1250    7.6276    1.0000   -0.0000
    8.7500    8.2526    1.0000    0.0000
    9.3750    8.8776    1.0000   -0.0000
   10.0000    9.5026    1.0000    0.0000

   Maximum estimated error by components
    6.92e-05    1.81e-05    6.42e-05