PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_quad_md_sgq_multi_vec (d01es)
Purpose
nag_quad_md_sgq_multi_vec (d01es) approximates a vector of definite integrals
over the unit hypercube
, given the vector of integrands
.
The function uses a sparse grid discretisation, allowing for computationally feasible estimations of integrals of high dimension ().
Syntax
[
dinest,
errest,
ivalid,
user,
ifail] = d01es(
ni,
f,
maxdlv,
iopts,
opts, 'ndim',
ndim, 'user',
user)
[
dinest,
errest,
ivalid,
user,
ifail] = nag_quad_md_sgq_multi_vec(
ni,
f,
maxdlv,
iopts,
opts, 'ndim',
ndim, 'user',
user)
Description
nag_quad_md_sgq_multi_vec (d01es) uses a sparse grid to generate a vector of approximations
to a vector of integrals
over the unit hypercube
, that is,
Comparing Quadrature Over Full and Sparse Grids
Before illustrating the sparse grid construction, it is worth comparing integration over a sparse grid to integration over a full grid.
Given a one-dimensional quadrature rule with abscissae, which accurately evaluates a polynomial of order , a full tensor product over dimensions, a full grid, may be constructed with multidimensional abscissae. Such a product will accurately integrate a polynomial where the maximum power of any dimension is . For example if and , such a rule will accurately integrate any polynomial whose highest order term is . Such a polynomial may be said to have a maximum combined order of , provided no individual dimension contributes a power greater than . However, the number of multidimensional abscissae, or points, required increases exponentially with the dimension, rapidly making such a construction unusable.
The sparse grid technique was developed by Smolyak (
Smolyak (1963)). In this, multiple one-dimensional quadrature rules of increasing accuracy are combined in such a way as to provide a multidimensional quadrature rule which will accurately evaluate the integral of a polynomial whose maximum order appears as a monomial. Hence a sparse grid construction whose highest level quadrature rule has polynomial order
will accurately integrate a polynomial whose maximum combined order is also
. Again taking
, one may, theoretically, accurately integrate a polynomial such as
, but not a polynomial such as
. Whilst this has a lower maximum combined order than the full tensor product, the number of abscissae required increases significantly slower than the equivalent full grid, making some classes of integrals of dimension
tractable. Specifically, if a one-dimensional quadrature rule of level
has
abscissae, the corresponding full grid will have
multidimensional abscissae, whereas the sparse grid will have
.
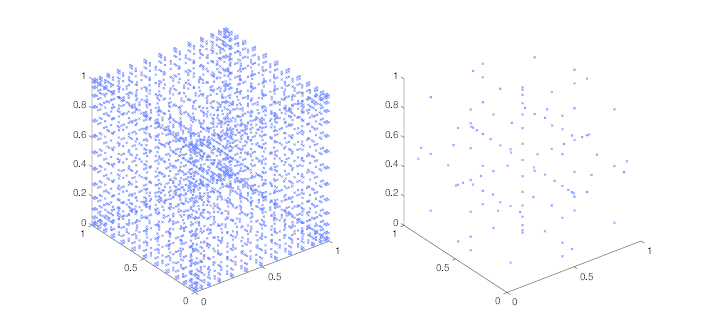
Figure 1 demonstrates this using a Gauss–Patterson rule with
points in
dimensions. The full grid requires
points, whereas the sparse grid only requires
.
Figure 1: Three-dimensional full (left) and sparse (right) grids, constructed from the point Gauss–Patterson rule
Sparse Grid Quadrature
We now include a brief description of the sparse grid construction, sufficient for the understanding of the use of this routine. For a more detailed analysis, see
Gerstner and Griebel (1998).
Consider a one-dimensional
-point quadrature rule of level
,
. The action of this rule on a integrand
is to approximate its definite one-dimensional integral
as,
using weights
and abscissae
, for
.
Now construct a set of one-dimensional quadrature rules, , such that the accuracy of the quadrature rule increases with the level number. In this routine we exclusively use quadrature rules which are completely nested, implying that if an abscissae is in level , it is also in level . The quantity denotes some maximum level appropriate to the rules that have been selected.
Now define the action of the tensor product of
rules as,
where the individual level indices
are not necessarily ordered or unique. Each tensor product of
rules defines an action of the quadrature rules
,
over a subspace, which is given a level
. If all rule levels are equal, this is the full tensor product of that level.
The sparse grid construction of level
can then be declared as the sum of all actions of the quadrature differences
, over all subspaces having a level at most
,
By definition, all subspaces used for level must also be used for level , and as such the difference between the result of all actions over subsequent sparse grid constructions may be used as an error estimate.
Let be the maximum level allowable in a sparse grid construction. The classical sparse grid construction of allows each dimension to support a one-dimensional quadrature rule of level at most , with such a quadrature rule being used in every dimension at least once. Such a construction lends equal weight to each dimension of the integration, and is termed here ‘isotropic’.
Define the set , where is the maximum quadrature rule allowed in the th dimension, and to be the maximum quadrature rule used by any dimension. Let a subspace be identified by its quadrature difference levels, .
The classical construction may be extended by allowing different dimensions to have different values , and by allowing . This creates non-isotropic constructions. These are especially useful in higher dimensions, where some dimensions contribute more than others to the result, as they can drastically reduce the number of function evaluations required.
For example, consider the two-dimensional construction with . The classical isotropic construction would have the following subspaces.
Subspaces generated by a classical sparse grid with
.
| Level |
Subspaces |
|
|
|
,
|
|
,
,
|
|
,
,
,
|
If the variation in the second dimension is sufficiently accurately described by a quadrature rule of level , the contributions of the subspaces and are probably negligible. Similarly, if the variation in the first dimension is sufficiently accurately described by a quadrature rule of level , the subspace is probably negligible. Furthermore the subspace would also probably have negligible impact, whereas the subspaces and would not. Hence restricting the first dimension to a maximum level of , and the second dimension to a maximum level of would probably give a sufficiently acceptable estimate, and would generate the following subspaces.
Subspaces generated by a non-isotropic sparse grid with
,
and
.
| Level |
Subspaces |
|
|
|
,
|
|
,
|
|
,
|
Taking this to the extreme, if the variation in the first and second dimensions are sufficiently accurately described by a level quadrature rule, restricting the maximum level of both dimensions to would generate the following subspaces.
Subspaces generated by a sparse grid construction with
,
and
.
| Level |
Subspaces |
|
|
|
,
|
|
|
|
None |
Hence one subspace is generated at level , and no subspaces are generated at level . The level subspace actually indicates that this is the full grid of level .
Using nag_quad_md_sgq_multi_vec (d01es)
nag_quad_md_sgq_multi_vec (d01es) uses optional parameters, supplied in the option arrays
iopts and
opts. Before calling
nag_quad_md_sgq_multi_vec (d01es), these option arrays must be initialized using
nag_quad_opt_set (d01zk). Once initialized, the required options may be set and queried using
nag_quad_opt_set (d01zk) and
nag_quad_opt_get (d01zl) respectively. A complete list of the options available may be found in
Optional Parameters.
You may control the maximum level required,
, using the optional parameter
Maximum Level. Furthermore, you may control the first level at which the error comparison will take place using the optional parameter
Minimum Level, allowing for the forced evaluation of a predetermined number of levels before the routine attempts to complete. Completion is flagged when the error estimate is sufficiently small:
where
and
are the absolute and relative error tolerances, respectively, and
is the highest level at which computation was performed. The tolerances
and
can be controlled by setting the optional parameters
Absolute Tolerance and
Relative Tolerance.
Owing to the interlacing nature of the quadrature rules used herein, abscissae
required in lower level subspaces will also appear in higher-level subspaces. This allows for calculations which will be repeated later to be stored and re-used. However, this is naturally at the expense of memory. It may also be at the expense of computational time, depending on the complexity of the integrands, as the lookup time for a given value is (at worst)
. Furthermore, as the sparse grid level increases, fewer subsequent levels will require values from the current level. You may control the number of levels for which values are stored by setting the optional parameter
Index Level.
Two different sets of interlacing quadrature rules are selectable using the optional parameter
Quadrature Rule: Gauss–Patterson and Clenshaw–Curtis. Gauss–Patterson rules offer greater polynomial accuracy, whereas Clenshaw–Curtis rules are often effective for oscillatory integrands. Clenshaw–Curtis rules require function values to be evaluated on the boundary of the hypercube, whereas Gauss–Patterson rules do not. Both of these rules use precomputed weights, and as such there is an effective limit on
; see the description of the optional parameter
Quadrature Rule. The value of
is returned by the queriable optional parameter
Maximum Quadrature Level.
nag_quad_md_sgq_multi_vec (d01es) also allows for non-isotropic sparse grids to be constructed. This is done by appropriately setting the array
maxdlv. It should be emphasised that a non-isometric construction should only be used if the integrands behave in a suitable way. For example, they may decay toward zero as the lesser dimensions approach their bounds of
. It should also be noted that setting
will not reduce the dimension of the integrals, it will simply indicate that only one point in dimension
should be used. It is also advisable to approximate the integrals several times, once with an isometric construction of some level, and then with a non-isometric construction with higher levels in various dimensions. If the difference between the solutions is significantly more than the returned error estimates, the assumptions of dimensional importance are probably incorrect.
The abscissae in each subspace are generally expressible in a sparse manner, because many of the elements of each abscissa will in fact be the centre point of the dimension, which is termed here the ‘trivial’ element. In this function the trivial element is always returned as
owing to the restriction to the
hypercube. As such, the function
f returns the abscissae in Compressed Column Storage (CCS) format (see the
F11 Chapter Introduction). This has particular advantages when using accelerator hardware to evaluate the required functions, as much less data must be forwarded. It also, potentially, allows for calculations to be computed faster, as any sub-calculations dependent upon the trivial value may be potentially re-used. See the example in
Example.
References
Caflisch R E, Morokoff W and Owen A B (1997) Valuation of mortgage backed securities using Brownian bridges to reduce effective dimension Journal of Computational Finance 1 27–46
Gerstner T and Griebel M (1998) Numerical integration using sparse grids Numerical Algorithms 18 209–232
Smolyak S A (1963) Quadrature and interpolation formulas for tensor products of certain classes of functions Dokl. Akad. Nauk SSSR 4 240–243
Parameters
Compulsory Input Parameters
- 1:
– int64int32nag_int scalar
-
, the number of integrands.
Constraint:
.
- 2:
– function handle or string containing name of m-file
-
f must return the value of the integrands
at a set of
-dimensional points
, implicitly supplied as columns of a matrix
. If
was supplied explicitly you would find that most of the elements attain the same value,
; the larger the number of dimensions, the greater the proportion of elements of
would be equal to
. So,
is effectively a sparse matrix, except that the ‘zero’ elements are replaced by elements that are all equal to the value
. For this reason
is supplied, as though it were a sparse matrix, in compressed column storage (CCS) format (see the
F11 Chapter Introduction).
Individual entries
of
, for
, are either trivially valued, in which case
, or are non-trivially valued. For point
, the non-trivial row indices and corresponding abscissae values are supplied in elements
, for
, of the arrays
irowix and
xs, respectively. Hence the
th column of the matrix
is retrievable as
An equivalent integer valued matrix
is also implicitly provided. This contains the unique indices
of the underlying one-dimensional quadrature rule corresponding to the individual abscissae
. For trivial abscissae, the implicit index
.
is supplied in the same CCS format as
, with the non-trivial values supplied in
qs.
[fm, iflag, user] = f(ni, ndim, nx, xtr, nntr, icolzp, irowix, xs, qs, iflag, user)
Input Parameters
- 1:
– int64int32nag_int scalar
-
, the number of integrands.
- 2:
– int64int32nag_int scalar
-
, the number of dimensions.
- 3:
– int64int32nag_int scalar
-
, the number of points , corresponding to the number of columns of , at which the set of integrands must be evaluated.
- 4:
– double scalar
-
, the value of the trivial elements of .
- 5:
– int64int32nag_int scalar
-
If
, the number of non-trivial elements of
.
If , the total number of abscissae from the underlying one-dimensional quadrature.
- 6:
– int64int32nag_int array
-
The set
contains the indices of
irowix and
xs corresponding to the non-trivial elements of column
of
and hence of the point
, for
.
- 7:
– int64int32nag_int array
-
The row indices corresponding to the non-trivial elements of .
- 8:
– double array
-
, the non-trivial entries of .
- 9:
– int64int32nag_int array
-
, the indices of the underlying quadrature rules corresponding to .
- 10:
– int64int32nag_int scalar
-
If
, this is the first call to
f.
, and the entire point
will satisfy
, for
. In addition,
nntr contains the total number of abscissae from the underlying one-dimensional quadrature;
xs contains the complete set of abscissae and
qs contains the corresponding quadrature indices, with
and
. This will always be called in serial.
In subsequent calls to
f,
. Subsequent calls may be made from within an OpenMP parallel region. See
Parallelism and Performance for details.
- 11:
– Any MATLAB object
f is called from
nag_quad_md_sgq_multi_vec (d01es) with the object supplied to
nag_quad_md_sgq_multi_vec (d01es).
Output Parameters
- 1:
– double array
-
, for and .
- 2:
– int64int32nag_int scalar
-
Set if you wish to force an immediate exit from nag_quad_md_sgq_multi_vec (d01es) with .
- 3:
– Any MATLAB object
- 3:
– int64int32nag_int array
Suggested value:
for all .
, the array of maximum levels for each dimension.
, for
, contains
, the maximum level of quadrature rule dimension
j will support.
The default value,
will be used if either
or
(for details on the default values for
and
and on how to change these values see the options
Maximum Level,
Maximum Quadrature Level and
Quadrature Rule).
If for all , only one evaluation will be performed, and as such no error estimation will be possible.
Note: setting non-default values for some dimensions makes the assumption that the contribution from the omitted subspaces is . The integral and error estimates will only be based on included subspaces, which if the contribution assumption is not valid will be erroneous.
- 4:
– int64int32nag_int array
- 5:
– double array
-
The arrays
iopts and
opts must not be altered between calls to any of the functions
nag_quad_md_sgq_multi_vec (d01es),
nag_quad_opt_set (d01zk) and
nag_quad_opt_get (d01zl).
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the array
maxdlv.
, the number of dimensions.
Constraint:
.
- 2:
– Any MATLAB object
user is not used by
nag_quad_md_sgq_multi_vec (d01es), but is passed to
f. Note that for large objects it may be more efficient to use a global variable which is accessible from the m-files than to use
user.
Output Parameters
- 1:
– double array
-
contains the final estimate of the definite integral , for .
- 2:
– double array
-
contains the final error estimate of the definite integral , for .
- 3:
– int64int32nag_int array
-
indicates the final state of integral
, for
.
- The error estimate for integral was below the requested tolerance.
- The error estimate for integral was below the requested tolerance. The final level used was non-isotropic.
- The error estimate for integral was above the requested tolerance.
- The error estimate for integral was above .
- You aborted the evaluation before an error estimate could be made.
- 4:
– Any MATLAB object
- 5:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Note: nag_quad_md_sgq_multi_vec (d01es) may return useful information for one or more of the following detected errors or warnings.
Errors or warnings detected by the function:
-
-
The requested accuracy was not achieved for at least one integral.
-
-
No accuracy was achieved for at least one integral.
-
-
Constraint: .
-
-
Constraint: .
-
-
Either the option arrays
iopts and
opts have not been initialized for
nag_quad_md_sgq_multi_vec (d01es), or they have become corrupted.
-
-
Exit requested from
f with
.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
For each integral
, an error estimate
is returned, where,
where
is the highest level at which computation was performed.
Further Comments
Not applicable.
Example
The example program evaluates an estimate to the set of integrals
where
.
Open in the MATLAB editor:
d01es_example
function d01es_example
fprintf('d01es example results\n\n');
ni = int64(10);
d = int64(4);
iopts = zeros(100,1,'int64');
opts = zeros(100,1);
[iopts, opts, ifail] = d01zk('Initialize = d01es', iopts, opts);
[iopts, opts, ifail] = d01zk('Absolute Tolerance = 0.0', iopts, opts);
[iopts, opts, ifail] = d01zk('Relative Tolerance = 1.0e-3', iopts, opts);
[iopts, opts, ifail] = d01zk('Maximum Level = 6', iopts, opts);
[iopts, opts, ifail] = d01zk('Index Level = 5', iopts, opts);
maxdlv = zeros(d,1,'int64');
[dinest, errest, ivalid, user, ifail] = d01es(ni, @f, maxdlv, iopts, opts);
fprintf('%10s%13s%13s%14s\n','integrand', 'integral','error','state');
for i = 1:ni
fprintf('%7d%16.6f%15.2e%10d\n',i,dinest(i),errest(i),ivalid(i));
end
function [fm, iflag, user] = ...
f(ni, ndim, nx, xtr, nntr, icolzp, irowix, xs, qs, iflag, user)
fm = zeros(ni,nx);
s_tr = xtr*double(ndim*(ndim+1))/2;
for i = 1:nx
i1 = icolzp(i);
i2 = icolzp(i+1)-1;
s_ntr = sum(double(irowix(i1:i2)).*(xs(i1:i2)-xtr));
for j = 1:ni
fm(j,i) = sin(double(j)+s_ntr+s_tr)*log(s_ntr+s_tr);
end
end
d01es example results
integrand integral error state
1 0.038352 2.40e-05 0
2 0.401177 1.70e-05 0
3 0.395161 5.66e-06 0
4 0.025836 2.31e-05 0
5 -0.367242 1.93e-05 0
6 -0.422680 2.25e-06 0
7 -0.089508 2.17e-05 0
8 0.325958 2.12e-05 0
9 0.441739 1.21e-06 0
10 0.151388 1.99e-05 0
Optional Parameters
Several optional parameters in
nag_quad_md_sgq_multi_vec (d01es) control aspects of the algorithm, methodology used, logic or output. Their values are contained in the arrays
iopts and
opts; these must be initialized before calling
nag_quad_md_sgq_multi_vec (d01es) by first calling
nag_quad_opt_set (d01zk) with
optstr set to
"Initialize = nag_quad_md_sgq_multi_vec (d01es)".
Each optional parameter has an associated default value; to set any of them to a non-default value, or to reset any of them to the default value, use
nag_quad_opt_set (d01zk). The current value of an optional parameter can be queried using
nag_quad_opt_get (d01zl).
The remainder of this section can be skipped if you wish to use the default values for all optional parameters.
The following is a list of the optional parameters available. A full description of each optional parameter is provided in
Description of the s.
Description of the Optional Parameters
For each option, we give a summary line, a description of the optional parameter and details of constraints.
The summary line contains:
- the keywords, where the minimum abbreviation of each keyword is underlined;
- a parameter value,
where the letters , and denote options that take character, integer and real values respectively.
- the default value.
The following symbol represent various machine constants:
All options accept the value ‘DEFAULT’ in order to return single options to their default states.
Keywords and character values are case insensitive, however they must be separated by at least one space.
Queriable options will return the appropriate value when queried by calling
nag_quad_opt_get (d01zl). They will have no effect if passed to
nag_quad_opt_set (d01zk).
For
nag_quad_md_sgq_multi_vec (d01es) the maximum length of the argument
cvalue used by
nag_quad_opt_get (d01zl) is
.
, the absolute tolerance required.
Index Level Default
The maximum level at which function values are stored for later use. Larger values use increasingly more memory, and require more time to access specific elements. Lower levels result in more repeated computation.
Constraint: .
Maximum Level Default
, the maximum number of levels to evaluate.
Constraint: .
Note: the maximum allowable level in any single dimension,
, is governed by the
Quadrature Rule selected. If a value greater than
is set, only a subset of subspaces from higher levels will be used. Should this subset be empty for a given level, computation will consider the preceding level to be the maximum level and will terminate.
Maximum Nx Default
, the maximum number of points to evaluate in a single call to
f.
Constraint: .
Maximum Quadrature Level Queriable only
, the maximum level of the underlying one-dimensional quadrature rule (see
Quadrature Rule).
The minimum number of levels which must be evaluated before an error estimate is used to determine convergence.
Constraint: .
Note: if the minimum level is greater than the maximum computable level, the maximum level will be used.
Quadrature Rule Default
The underlying one-dimensional quadrature rule to be used in the construction. Open rules do not require evaluations at boundaries.
- or
- The interlacing Gauss–Patterson rules. Level uses abscissae. All levels are open. These rules provide high order accuracy. .
- or
- The interlacing Clenshaw–Curtis rules. Level uses abscissae. All levels above level are closed. .
, the relative tolerance required.
Summation Precision Default
Determines whether
nag_quad_md_sgq_multi_vec (d01es) uses working precision or higher-than-working precision to accumulate the actions over subspaces.
- or
- Higher-than-working precision is used to accumulate the action over a subspace, and for the accumulation of all such actions. This is more expensive computationally, although this is probably negligible in comparison to the cost of evaluating the integrands and the overall runtime. This significantly reduces variation in the result when changing the number of threads.
- or
- Working precision is used to accumulate the actions over subspaces. This may provide some speedup, particularly if or is large. The results of parallel simulations will however be more prone to variation.
Note: the following option is relevant only to multithreaded implementations of the NAG Library..
Serial Levels Default
, the number of levels to be evaluated in serial before initializing parallelization. For relatively trivial integrands, this may need to be set greater than the default to reduce parallel overhead.
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015