PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_fit_1dcheb_deriv (e02ah)
Purpose
nag_fit_1dcheb_deriv (e02ah) determines the coefficients in the Chebyshev series representation of the derivative of a polynomial given in Chebyshev series form.
Syntax
Description
nag_fit_1dcheb_deriv (e02ah) forms the polynomial which is the derivative of a given polynomial. Both the original polynomial and its derivative are represented in Chebyshev series form. Given the coefficients
, for
, of a polynomial
of degree
, where
the function returns the coefficients
, for
, of the polynomial
of degree
, where
Here
denotes the Chebyshev polynomial of the first kind of degree
with argument
. It is assumed that the normalized variable
in the interval
was obtained from your original variable
in the interval
by the linear transformation
and that you require the derivative to be with respect to the variable
. If the derivative with respect to
is required, set
and
.
Values of the derivative can subsequently be computed, from the coefficients obtained, by using
nag_fit_1dcheb_eval2 (e02ak).
The method employed is that of Chebyshev series (see Chapter 8 of
Modern Computing Methods (1961)), modified to obtain the derivative with respect to
. Initially setting
, the function forms successively
References
Modern Computing Methods (1961) Chebyshev-series NPL Notes on Applied Science 16 (2nd Edition) HMSO
Parameters
Compulsory Input Parameters
- 1:
– int64int32nag_int scalar
-
, the degree of the given polynomial .
Constraint:
.
- 2:
– double scalar
- 3:
– double scalar
-
The lower and upper end points respectively of the interval
. The Chebyshev series representation is in terms of the normalized variable
, where
Constraint:
.
- 4:
– double array
-
la, the dimension of the array, must satisfy the constraint
.
The Chebyshev coefficients of the polynomial
. Specifically, element
of
a must contain the coefficient
, for
. Only these
elements will be accessed.
Unchanged on exit, but see
adif, below.
- 5:
– int64int32nag_int scalar
-
The index increment of
a. Most frequently the Chebyshev coefficients are stored in adjacent elements of
a, and
ia1 must be set to
. However, if for example, they are stored in
, then the value of
ia1 must be
. See also
Further Comments.
Constraint:
.
- 6:
– int64int32nag_int scalar
-
The index increment of
adif. Most frequently the Chebyshev coefficients are required in adjacent elements of
adif, and
iadif1 must be set to
. However, if, for example, they are to be stored in
, then the value of
iadif1 must be
. See
Further Comments.
Constraint:
.
Optional Input Parameters
None.
Output Parameters
- 1:
– double scalar
-
The value of
. If this value is passed to the integration function
nag_fit_1dcheb_integ (e02aj) with the coefficients of
, then the original polynomial
is recovered, including its constant coefficient.
- 2:
– double array
-
.
The Chebyshev coefficients of the derived polynomial
. (The differentiation is with respect to the variable
.) Specifically, element
of
adif contains the coefficient
, for
. Additionally, element
is set to zero. A call of the function may have the array name
adif the same as
a, provided that note is taken of the order in which elements are overwritten, when choosing the starting elements and increments
ia1 and
iadif1, i.e., the coefficients
must be intact after coefficient
is stored. In particular, it is possible to overwrite the
completely by having
, and the actual arrays for
a and
adif identical.
- 3:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
| On entry, | , |
| or | , |
| or | , |
| or | , |
| or | , |
| or | . |
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
There is always a loss of precision in numerical differentiation, in this case associated with the multiplication by
in the formula quoted in
Description.
Further Comments
The time taken is approximately proportional to .
The increments
ia1,
iadif1 are included as arguments to give a degree of flexibility which, for example, allows a polynomial in two variables to be differentiated with respect to either variable without rearranging the coefficients.
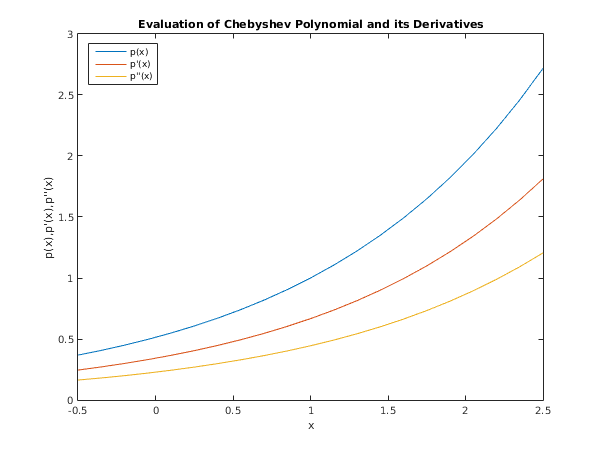
Example
Suppose a polynomial has been computed in Chebyshev series form to fit data over the interval
. The following program evaluates the first and second derivatives of this polynomial at
equally spaced points over the interval. (For the purposes of this example,
xmin,
xmax and the Chebyshev coefficients are simply supplied
.
Normally a program would first read in or generate data and compute the fitted polynomial.)
Open in the MATLAB editor:
e02ah_example
function e02ah_example
fprintf('e02ah example results\n\n');
xmin = -0.5; xmax = 2.5;
a = [2.53213 1.13032 0.2715 0.04434 0.00547 0.00054 4e-05];
n = int64(6);
ia1 = int64(1);
iadif1 = int64(1);
[patm1, adif, ifail] = e02ah( ...
n, xmin, xmax, a, ia1, iadif1);
[patm1, adif2, ifail] = e02ah( ...
n, xmin, xmax, adif, ia1, iadif1);
m = 21;
dx = (xmax-xmin)/(m-1);
x = [xmin:dx:xmax];
for i = 1:m
[fit0(i), ifail] = e02ak( ...
n, xmin, xmax, a, ia1, x(i));
[fit1(i), ifail] = e02ak( ...
n-1, xmin, xmax, adif, iadif1, x(i));
[fit2(i), ifail] = e02ak( ...
n-2, xmin, xmax, adif2, iadif1, x(i));
end
sol = [x; fit0; fit1; fit2];
fprintf(' x p(x) p''(x) p''''(x)\n');
fprintf('%9.4f %9.4f %9.4f %9.4f\n',sol(1:4,1:5:21));
fig1 = figure;
plot(x,fit0,x,fit1,x,fit2);
title('Evaluation of Chebyshev Polynomial and its Derivatives');
xlabel('x');
ylabel('p(x),p''(x),p''''(x)');
legend('p(x)', 'p''(x)', 'p''''(x)','Location','NorthWest');
e02ah example results
x p(x) p'(x) p''(x)
-0.5000 0.3679 0.2453 0.1637
0.2500 0.6065 0.4043 0.2696
1.0000 1.0000 0.6667 0.4444
1.7500 1.6487 1.0992 0.7329
2.5000 2.7183 1.8119 1.2056
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015