| On entry, | ; |
| or | ; |
| or | ; |
| or | or for some and ; |
| or | for some ; |
| or | or for some and ; |
| or | or or for some ; |
| or | ; |
| or | , , , , or for some ; |
| or | . |
Open in the MATLAB editor: d06da_example
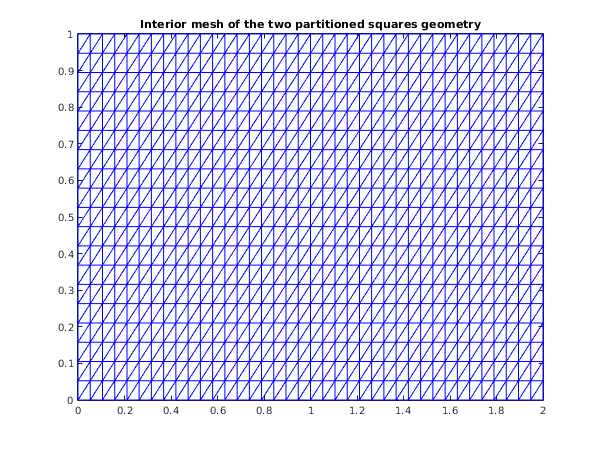
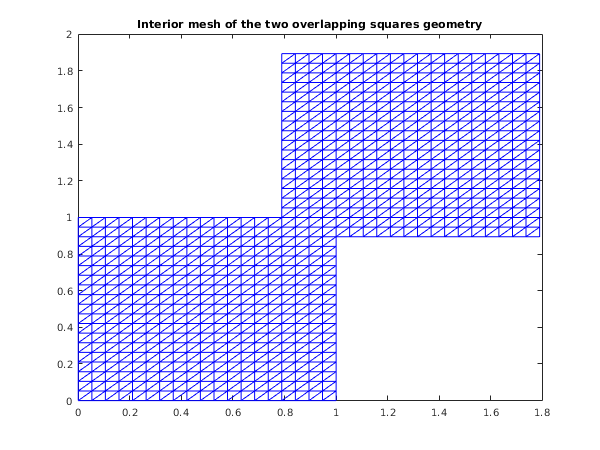
function d06da_example fprintf('d06da example results\n\n'); coor1 = zeros(2,400); for j = 1:20 for i = 1:20 coor1(1,(j-1)*20+i) = (i-1)/19; coor1(2,(j-1)*20+i) = (j-1)/19; end end edge1 = ones(3, 76, 'int64'); edge1(1, 1:76) = int64([1:19,20*(1:19),401-(1:19),401-20*(1:19)]); edge1(2, 1:76) = int64([2:19,20*(1:19),401-(1:19),401-20*(1:19),1]); conn1 = zeros(3, 722, 'int64'); ind = -1; for i=1:379 if (rem(i, 20) ~= 0) ind = ind+2; conn1(1, ind) = int64(i); conn1(1, ind+1) = int64(i); conn1(2, ind) = int64(i+1); conn1(2, ind+1) = int64(i+21); conn1(3, ind) = int64(i+21); conn1(3, ind+1) = int64(i+20); end end reft1 = ones(722, 1, 'int64'); reft2 = reft1; reft2(:) = int64(2); itype = [int64(1)]; itrace = int64(1); % Transform the first domain to obtain an overlapping second domain trans = [15/19; 17/19; 0; 0; 0; 0]; [coor1, edge1, conn1, coor2, edge2, conn2, ifail] = ... d06da( ... itype, trans, coor1, edge1, conn1, itrace); % Restitch the meshes [nv3, nelt3, nedge3, coor3, edge3, conn3, reft3, ifail] = ... d06db( ... coor1, edge1, conn1, reft1, coor2, edge2, conn2, reft2, itrace); % Plot the result fig1 = figure; triplot(transpose(double(conn3(:,1:nelt3))), coor3(1,:), coor3(2,:)); title ('Interior mesh of the two overlapping squares geometry'); % Now consider a partitioned second domain trans = [1; 0; 0; 0; 0; 0]; [coor1, edge1, conn1, coor2, edge2, conn2, ifail] = ... d06da( ... itype, trans, coor1, edge1, conn1, itrace); % Restitch the meshes [nv3, nelt3, nedge3, coor3, edge3, conn3, reft3, ifail] = ... d06db( ... coor1, edge1, conn1, reft1, coor2, edge2, conn2, reft2, itrace); % Plot the result fig2 = figure; triplot(transpose(double(conn3(:,1:nelt3))), coor3(1,:), coor3(2,:)); title ('Interior mesh of the two partitioned squares geometry');
d06da example results
Transformation 1: translation
translation vector: 0.7895 0.8947
Final transformation matrix y = A*x + b:
1.000 0.000 0.7895
0.000 1.000 0.8947
Transformation 1: translation
translation vector: 1.000 0.000
Final transformation matrix y = A*x + b:
1.000 0.000 1.000
0.000 1.000 0.000