NAG Toolbox: nag_mesh_2d_join (d06db)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{coor1}\left(2,\mathbf{nv1}\right)$ – double array

$\mathbf{coor1}\left(1,\mathit{i}\right)$ contains the $x$ coordinate of the $\mathit{i}$th vertex of the first input mesh, for $\mathit{i}=1,2,\dots ,\mathbf{nv1}$; while $\mathbf{coor1}\left(2,\mathit{i}\right)$ contains the corresponding $y$ coordinate.

2:     $\mathrm{edge1}\left(3,\mathbf{nedge1}\right)$ – int64int32nag_int array

The specification of the boundary edges of the first input mesh. $\mathbf{edge1}\left(1,j\right)$ and $\mathbf{edge1}\left(2,j\right)$ contain the vertex numbers of the two end points of the $j$th boundary edge. $\mathbf{edge1}\left(3,j\right)$ is a user-supplied tag for the $j$th boundary edge.

Constraint: $1\le \mathbf{edge1}\left(\mathit{i},\mathit{j}\right)\le \mathbf{nv1}$ and $\mathbf{edge1}\left(1,\mathit{j}\right)\ne \mathbf{edge1}\left(2,\mathit{j}\right)$, for $\mathit{i}=1,2$ and $\mathit{j}=1,2,\dots ,\mathbf{nedge1}$.

3:     $\mathrm{conn1}\left(3,\mathbf{nelt1}\right)$ – int64int32nag_int array

The connectivity between triangles and vertices of the first input mesh. For each triangle $\mathit{j}$, $\mathbf{conn1}\left(\mathit{i},\mathit{j}\right)$ gives the indices of its three vertices (in anticlockwise order), for $\mathit{i}=1,2,3$ and $\mathit{j}=1,2,\dots ,\mathbf{nelt1}$.

Constraints:

• $1\le \mathbf{conn1}\left(i,j\right)\le \mathbf{nv1}$;
• $\mathbf{conn1}\left(1,j\right)\ne \mathbf{conn1}\left(2,j\right)$;
• $\mathbf{conn1}\left(1,\mathit{j}\right)\ne \mathbf{conn1}\left(3,\mathit{j}\right)$ and $\mathbf{conn1}\left(2,\mathit{j}\right)\ne \mathbf{conn1}\left(3,\mathit{j}\right)$, for $\mathit{i}=1,2,3$ and $\mathit{j}=1,2,\dots ,\mathbf{nelt1}$.

4:     $\mathrm{reft1}\left(\mathbf{nelt1}\right)$ – int64int32nag_int array

$\mathbf{reft1}\left(\mathit{k}\right)$ contains the user-supplied tag of the $\mathit{k}$th triangle from the first input mesh, for $\mathit{k}=1,2,\dots ,\mathbf{nelt1}$.

5:     $\mathrm{coor2}\left(2,\mathbf{nv2}\right)$ – double array

$\mathbf{coor2}\left(1,\mathit{i}\right)$ contains the $x$ coordinate of the $\mathit{i}$th vertex of the second input mesh, for $\mathit{i}=1,2,\dots ,\mathbf{nv2}$; while $\mathbf{coor2}\left(2,\mathit{i}\right)$ contains the corresponding $y$ coordinate.

6:     $\mathrm{edge2}\left(3,\mathbf{nedge2}\right)$ – int64int32nag_int array

The specification of the boundary edges of the second input mesh. $\mathbf{edge2}\left(1,j\right)$ and $\mathbf{edge2}\left(2,j\right)$ contain the vertex numbers of the two end points of the $j$th boundary edge. $\mathbf{edge2}\left(3,j\right)$ is a user-supplied tag for the $j$th boundary edge.

Constraint: $1\le \mathbf{edge2}\left(\mathit{i},\mathit{j}\right)\le \mathbf{nv2}$ and $\mathbf{edge2}\left(1,\mathit{j}\right)\ne \mathbf{edge2}\left(2,\mathit{j}\right)$, for $\mathit{i}=1,2$ and $\mathit{j}=1,2,\dots ,\mathbf{nedge2}$.

7:     $\mathrm{conn2}\left(3,\mathbf{nelt2}\right)$ – int64int32nag_int array

The connectivity between triangles and vertices of the second input mesh. For each triangle $\mathit{j}$, $\mathbf{conn2}\left(\mathit{i},\mathit{j}\right)$ gives the indices of its three vertices (in anticlockwise order), for $\mathit{i}=1,2,3$ and $\mathit{j}=1,2,\dots ,\mathbf{nelt2}$.

Constraints:

• $1\le \mathbf{conn2}\left(i,j\right)\le \mathbf{nv2}$;
• $\mathbf{conn2}\left(1,j\right)\ne \mathbf{conn2}\left(2,j\right)$;
• $\mathbf{conn2}\left(1,\mathit{j}\right)\ne \mathbf{conn2}\left(3,\mathit{j}\right)$ and $\mathbf{conn2}\left(2,\mathit{j}\right)\ne \mathbf{conn2}\left(3,\mathit{j}\right)$, for $\mathit{i}=1,2,3$ and $\mathit{j}=1,2,\dots ,\mathbf{nelt2}$.

8:     $\mathrm{reft2}\left(\mathbf{nelt2}\right)$ – int64int32nag_int array

$\mathbf{reft2}\left(\mathit{k}\right)$ contains the user-supplied tag of the $\mathit{k}$th triangle from the second input mesh, for $\mathit{k}=1,2,\dots ,\mathbf{nelt2}$.

9:     $\mathrm{itrace}$ – int64int32nag_int scalar

The level of trace information required from nag_mesh_2d_join (d06db).

$\mathbf{itrace}\le 0$

No output is generated.

$\mathbf{itrace}\ge 1$

Details about the common vertices, edges and triangles to both meshes are printed on the current advisory message unit (see nag_file_set_unit_advisory (x04ab)).

Optional Input Parameters

1:     $\mathrm{eps}$ – double scalar

Default: $0.001$.

The relative precision of the restitching of the two input meshes (see Further Comments).

Constraint: $\mathbf{eps}>0.0$.

2:     $\mathrm{nv1}$ – int64int32nag_int scalar

Default: the dimension of the array coor1.

The total number of vertices in the first input mesh.

Constraint: $\mathbf{nv1}\ge 3$.

3:     $\mathrm{nelt1}$ – int64int32nag_int scalar

Default: the dimension of the arrays conn1, reft1. (An error is raised if these dimensions are not equal.)

The number of triangular elements in the first input mesh.

Constraint: $\mathbf{nelt1}\le 2\times \mathbf{nv1}-1$.

4:     $\mathrm{nedge1}$ – int64int32nag_int scalar

Default: the dimension of the array edge1.

The number of boundary edges in the first input mesh.

Constraint: $\mathbf{nedge1}\ge 1$.

5:     $\mathrm{nv2}$ – int64int32nag_int scalar

Default: the dimension of the array coor2.

The total number of vertices in the second input mesh.

Constraint: $\mathbf{nv2}\ge 3$.

6:     $\mathrm{nelt2}$ – int64int32nag_int scalar

Default: the dimension of the arrays conn2, reft2. (An error is raised if these dimensions are not equal.)

The number of triangular elements in the second input mesh.

Constraint: $\mathbf{nelt2}\le 2\times \mathbf{nv2}-1$.

7:     $\mathrm{nedge2}$ – int64int32nag_int scalar

Default: the dimension of the array edge2.

The number of boundary edges in the second input mesh.

Constraint: $\mathbf{nedge2}\ge 1$.

Output Parameters

1:     $\mathrm{nv3}$ – int64int32nag_int scalar

The total number of vertices in the resulting mesh.

2:     $\mathrm{nelt3}$ – int64int32nag_int scalar

The number of triangular elements in the resulting mesh.

3:     $\mathrm{nedge3}$ – int64int32nag_int scalar

The number of boundary edges in the resulting mesh.

4:     $\mathrm{coor3}\left(2,:\right)$ – double array

The second dimension of the array coor3 will be $\mathbf{nv1}+\mathbf{nv2}$.

$\mathbf{coor3}\left(1,\mathit{i}\right)$ will contain the $x$ coordinate of the $\mathit{i}$th vertex of the resulting mesh, for $\mathit{i}=1,2,\dots ,\mathbf{nv3}$; while $\mathbf{coor3}\left(2,i\right)$ will contain the corresponding $y$ coordinate.

5:     $\mathrm{edge3}\left(3,:\right)$ – int64int32nag_int array

The second dimension of the array edge3 will be $\mathbf{nedge1}+\mathbf{nedge2}$. This may be reduced to $\mathbf{nedge3}$ once that value is known.

The specification of the boundary edges of the resulting mesh. $\mathbf{edge3}\left(i,j\right)$ will contain the vertex number of the $i$th end point ($i=1,2$) of the $j$th boundary or interface edge.

If the two meshes overlap, $\mathbf{edge3}\left(3,j\right)$ will contain the same tag as the corresponding edge belonging to the first and/or the second input mesh.

If the two meshes are adjacent,

(i)	if the $j$th edge is part of the partition interface, then $\mathbf{edge3}\left(3,j\right)$ will contain the value $1000\times k_1+k_2$ where $k_1$ and $k_2$ are the tags for the same edge of the first and the second mesh respectively;
(ii)	otherwise, $\mathbf{edge3}\left(3,j\right)$ will contain the same tag as the corresponding edge belonging to the first and/or the second input mesh.

6:     $\mathrm{conn3}\left(3,:\right)$ – int64int32nag_int array

The second dimension of the array conn3 will be $\mathbf{nelt1}+\mathbf{nelt2}$. This may be reduced to $\mathbf{nelt3}$ once that value is known.

The connectivity between triangles and vertices of the resulting mesh. $\mathbf{conn3}\left(\mathit{i},\mathit{j}\right)$ will give the indices of its three vertices (in anticlockwise order), for $\mathit{i}=1,2,3$ and $\mathit{j}=1,2,\dots ,\mathbf{nelt3}$.

7:     $\mathrm{reft3}\left(:\right)$ – int64int32nag_int array

The dimension of the array reft3 will be $\mathbf{nelt1}+\mathbf{nelt2}$. This may be reduced to $\mathbf{nelt3}$ once that value is known

If the two meshes form a partition, $\mathbf{reft3}\left(\mathit{k}\right)$ will contain the same tag as the corresponding triangle belonging to the first or the second input mesh, for $\mathit{k}=1,2,\dots ,\mathbf{nelt3}$. If the two meshes overlap, then $\mathbf{reft3}\left(\mathit{k}\right)$ will contain the value $1000\times {\mathit{k}}_1+{\mathit{k}}_2$ where ${\mathit{k}}_1$ and ${\mathit{k}}_2$ are the user-supplied tags for the same triangle of the first and the second mesh respectively, for $\mathit{k}=1,2,\dots ,\mathbf{nelt3}$.

8:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

   $\mathbf{ifail}=1$

On entry,	$\mathbf{eps}\le 0.0$,
or	$\mathbf{nv1}<3$,
or	$\mathbf{nelt1}>2\times \mathbf{nv1}-1$,
or	$\mathbf{nedge1}<1$,
or	$\mathbf{edge1}\left(i,j\right)<1$ or $\mathbf{edge1}\left(i,j\right)>\mathbf{nv1}$ for some $i=1,2$ and $j=1,2,\dots ,\mathbf{nedge1}$,
or	$\mathbf{edge1}\left(1,j\right)=\mathbf{edge1}\left(2,j\right)$ for some $j=1,2,\dots ,\mathbf{nedge1}$,
or	$\mathbf{conn1}\left(i,j\right)<1$ or $\mathbf{conn1}\left(i,j\right)>\mathbf{nv1}$ for some $i=1,2,3$ and $j=1,2,\dots ,\mathbf{nelt1}$,
or	$\mathbf{conn1}\left(1,j\right)=\mathbf{conn1}\left(2,j\right)$ or $\mathbf{conn1}\left(1,j\right)=\mathbf{conn1}\left(3,j\right)$ or $\mathbf{conn1}\left(2,j\right)=\mathbf{conn1}\left(3,j\right)$ for some $j=1,2,\dots ,\mathbf{nelt1}$,
or	$\mathbf{nv2}<3$,
or	$\mathbf{nelt2}>2\times \mathbf{nv2}-1$,
or	$\mathbf{nedge2}<1$,
or	$\mathbf{edge2}\left(i,j\right)<1$ or $\mathbf{edge2}\left(i,j\right)>\mathbf{nv2}$ for some $i=1,2$ and $j=1,2,\dots ,\mathbf{nedge2}$,
or	$\mathbf{edge2}\left(1,j\right)=\mathbf{edge2}\left(2,j\right)$ for some $j=1,2,\dots ,\mathbf{nedge2}$,
or	$\mathbf{conn2}\left(i,j\right)<1$ or $\mathbf{conn2}\left(i,j\right)>\mathbf{nv2}$ for some $i=1,2,3$ and $j=1,2,\dots ,\mathbf{nelt2}$,
or	$\mathbf{conn2}\left(1,j\right)=\mathbf{conn2}\left(2,j\right)$ or $\mathbf{conn2}\left(1,j\right)=\mathbf{conn2}\left(3,j\right)$ or $\mathbf{conn2}\left(2,j\right)=\mathbf{conn2}\left(3,j\right)$ for some $j=1,2,\dots ,\mathbf{nelt2}$,
or	$\mathit{liwork}<2\times \mathbf{nv1}+3\times \mathbf{nv2}+\mathbf{nelt1}+\mathbf{nelt2}+\mathbf{nedge1}+\mathbf{nedge2}+1024$.

   $\mathbf{ifail}=2$

Using the input precision eps, the function has detected fewer than two coincident vertices between the two input meshes. You are advised to try another value of eps; if this error still occurs the two meshes are probably not stitchable.

   $\mathbf{ifail}=3$

A serious error has occurred in an internal call to the restitching function. You should check the input of the two meshes, especially the edge/vertex and/or the triangle/vertex connectivities. If the problem persists, contact NAG.

   $\mathbf{ifail}=4$

The function has detected a different number of coincident triangles from the two input meshes in the overlapping zone. You should check the input of the two meshes, especially the triangle/vertex connectivities.

   $\mathbf{ifail}=5$

The function has detected a different number of coincident edges from the two meshes on the partition interface. You should check the input of the two meshes, especially the edge/vertex connectivities.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: d06db_example

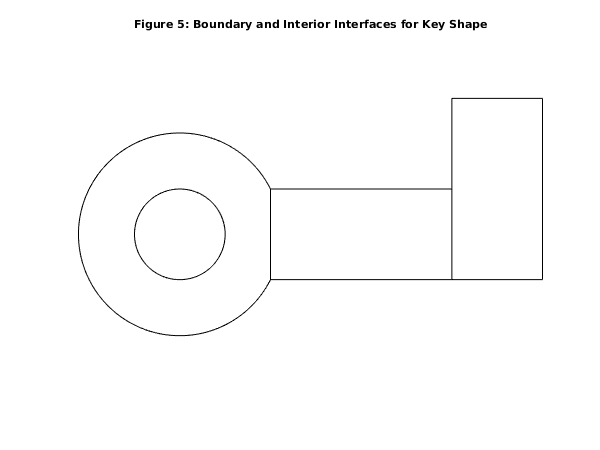
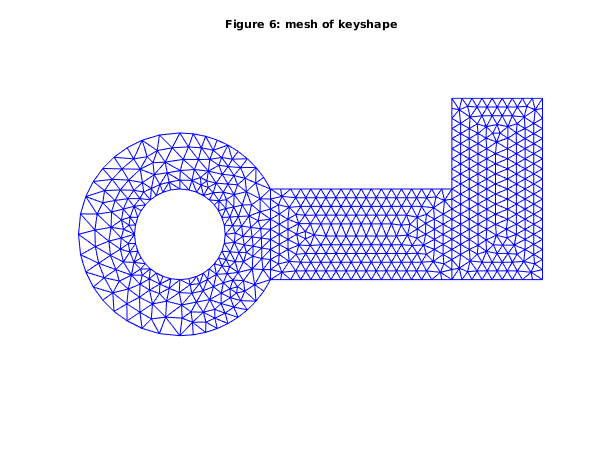
function d06db_example


fprintf('d06db example results\n\n');

d06db_ex1;
d06db_ex2;



function d06db_ex1

  fprintf('Example 1\n\n');
  n = 20;
  coor1 = zeros(2,n^2);
  dx = [0:1/(n-1):1];
  for j = 1:n
    coor1(1,(j-1)*n+1:j*n) = dx;
    coor1(2,(j-1)*n+1:j*n) = dx(j);
  end
  edge1 = ones(3, 4*n-4, 'int64');
  ind = int64(1:n-1);
  edge1(1, 1:(4*n-4)) = [ind,n*ind,n^2+1-ind,n^2+1-n*ind];
  edge1(2, 1:(4*n-5)) = edge1(1, 2:(4*n-4));
  edge1(2, 4*n-4)     = edge1(1, 1);
  conn1 = zeros(3, 2*(n-1)^2, 'int64');

  k = 0;
  l = int64(0);
  for i=1:n-1
    for j=1:n-1
       l = l + 1;
       k = k + 1;
       conn1(1, k) = l;
       conn1(2, k) = l + 1;
       conn1(3, k) = l + n + 1;
       k = k + 1;
       conn1(1, k) = l;
       conn1(2, k) = l + n + 1;
       conn1(3, k) = l + n;
    end
    l = l + 1;
  end
  reft1 = ones(2*(n-1)^2, 1, 'int64');
  reft2 = reft1;
  reft2(:) = int64(2);
  itype = [int64(1)];
  itrace = int64(1);

  for ktrans = 1:2
    if ktrans==2
      % Transform the first domain to obtain an overlapping second domain
      a = (n-5)/(n-1);
      b = (n-3)/(n-1);
      trans = [a; b; 0; 0; 0; 0];
      % plot boundary for partitioned geometry 
      fig3 = figure;
      plot([0 1  1 0 0], [0 0 1 1 0], 'black', ...
           [a a+1 a+1 a a],[b b b+1 b+1 b],'black')
      axis off
      axis equal
      title('Figure 3: Boundary of overlapping squares');
      fig4 = figure;
    else
      % Domains partition
      trans = [1; 0; 0; 0; 0; 0];
      % plot boundary for partitioned geometry 
      fig1 = figure;
      plot([0 2  2 0 0],[0 0 1 1 0],'black',[1 1],[0, 1],'black')
      axis off
      axis equal
      title('Figure 1: Boundary of partitioned squares');
      fig2 = figure;
    end
    [coor1, edge1, conn1, coor2, edge2, conn2, ifail] = ...
    d06da( ...
           itype, trans, coor1, edge1, conn1, itrace);

    % Restitch the meshes
    [nv3, nelt3, nedge3, coor3, edge3, conn3, reft3, ifail] = ...
    d06db( ...
           coor1, edge1, conn1, reft1, coor2, edge2, conn2, reft2, itrace);

    % Plot the result
    triplot(transpose(double(conn3(:,1:nelt3))), coor3(1,:), coor3(2,:));
    axis equal;
    axis off;
    if ktrans==2
      title ('Figure 4: mesh for two overlapping squares');
    else
      title ('Figure 2: mesh for two partitioned squares');
    end

  end
function d06db_ex2

  fprintf('\n\nExample 2\n\n');

  % First Geometry
  % -----------------------------------------------------------
  nlines = 9;
  % Characteristic points of the boundary mesh
  coorch = [ 2   2   1  -1  -2.2361   0.0000   0   0   0.0000;
            -1   1   0   0   0.0000  -2.2361  -1   1   2.2361];
  % Lines of the boundary mesh
  n10 = int64(10);
  line = [n10 10 10 10 10 10 10 10 10;
            1  2  9  5  6  3  8  4  7;
            2  9  5  6  1  8  4  7  3;
            0  2  2  2  2  1  1  1  1];
  rate = ones(nlines,1);
  % number of connected components
  ncomp = 2;
  nlcomp = int64([5; -4]);
  lcomp = ones(nlines,1,'int64');
  lcomp(1:nlcomp(1))        = [1   2   3   4   5];
  lcomp(nlcomp(1)+1:nlines) = [9   8   7   6];

  % Generate boundary mesh
  nvmax = int64(700);
  nedmx = int64(200);
  itrace = int64(0);
  crus = [0; 0];
  [nvb1, coor1, nedge1, edge1, user, ifail] = ...
  d06ba( ...
         coorch, line, @fbnd, crus, rate, nlcomp, lcomp, nvmax, ...
         nedmx, itrace);

  % Generate mesh using Delaunay-Voronoi method
  weight = [];
  npropa = int64(1);
  [nv1, nelt1, coor1, conn1, ifail] = ...
  d06ab( ...
         nvb1, edge1, coor1, weight, npropa, itrace, 'nedge', nedge1);

  % Smooth
  numfix = int64([0]);
  nqint = int64(0);
  [coor1, ifail] = d06ca( ...
                          coor1, edge1, conn1, numfix, itrace, nqint, ...
                          'nv', nv1, 'nelt', nelt1, 'nedge', nedge1, ...
                          'nvfix', int64(0));
  
  % Second Geometry
  % -----------------------------------------------------------
  nlines = 4;
  % Characteristic points of the boundary mesh
  coorch = [ 2   6   6   2;
            -1  -1   1   1];
  % Lines of the boundary mesh
  n19 = int64(19);
  line = [n19 10 19 10;
            1  2  3  4;
            2  3  4  1;
            0  0  0  0];
  rate = ones(nlines,1);
  % number of connected components
  ncomp = 1;
  nlcomp = [int64(4)];
  lcomp = int64([1   2   3   4]);

  % Generate boundary mesh
  [nvb2, coor2, nedge2, edge2, user, ifail] = ...
  d06ba( ...
         coorch, line, @fbnd, crus, rate, nlcomp, lcomp, nvmax, ...
         nedmx, itrace);
  % Generate mesh using Advancing Front method
  [nv2, nelt2, coor2, conn2, ifail] = ...
  d06ac( ...
         nvb2, edge2, coor2, weight, itrace, 'nedge', nedge2);

  % Third Geometry (rotation and translation of second)
  % -----------------------------------------------------------
  itype = [int64(3)];
  trans = [6; -1; -90; 0; 0; 0];
  [coor3, edge3, conn3, coor3, edge3, conn3, ifail] = ...
  d06da( ...
         itype, trans, coor2, edge2, conn2, itrace, 'nv', nv2, ...
         'nelt', nelt2, 'nedge', nedge2);
  
  % -----------------------------------------------------------
  % Combine 3 meshes
  % -----------------------------------------------------------
  % Restitch 1 and 2 to form mesh 4
  reft1(1:nelt1) = int64(1);
  reft2(1:nelt2) = int64(2);
  [nv4, nelt4, nedge4, coor4, edge4, conn4, reft4, ifail] = ...
  d06db( ...
         coor1, edge1, conn1, reft1, coor2, edge2, conn2, reft2, itrace, ...
         'nv1', nv1, 'nelt1', nelt1, 'nedge1', nedge1, ...
         'nv2', nv2, 'nelt2', nelt2, 'nedge2', nedge2);

  % Restitch 3 and 4 to form mesh 5
  reft3(1:nelt2) = int64(3);
  [nv5, nelt5, nedge5, coor5, edge5, conn5, reft5, ifail] = ...
  d06db( ...
         coor4, edge4, conn4, reft4, coor3, edge3, conn3, reft3, itrace, ...
         'nv1', nv4, 'nelt1', nelt4, 'nedge1', nedge4, ...
         'nv2', nv2, 'nelt2', nelt2, 'nedge2', nedge2);

  fprintf(' The restitched mesh characteristics\n');
  fprintf(' nv    = %5d\n', nv5);
  fprintf(' nelt  = %5d\n', nelt5);
  fprintf(' nedge = %5d\n', nedge5);

  % Plot boundary
  fig5 = figure;
  a = asin(1/sqrt(5));
  t1 = linspace(a, 2*pi-a, 100);
  t2 = linspace(0, 2*pi, 100);
  hold on
  r = sqrt(5);
  plot(r*cos(t1),r*sin(t1),'black');
  r = 1;
  plot(r*cos(t2),r*sin(t2),'black');
  plot([2 6 6 2 2],[-1 -1 1 1 -1],'black');
  plot([6 8 8 6 6],[-1 -1 3 3 -1],'black');
  axis off
  axis equal
  title('Figure 5: Boundary and Interior Interfaces for Key Shape'); 

  % Plot mesh
  fig6 = figure;
  triplot(transpose(double(conn5(:,1:nelt5))), coor5(1,:), coor5(2,:));
  axis equal;
  axis off;
  title ('Figure 6: mesh of keyshape');
function [result, user] = fbnd(i, x, y, user)
  result = 0;
  if (i == 1)
    % inner circle
    result = x^2 + y^2 - 1;
  elseif (i == 2)
    % outer circle
    result = x^2 + y^2 - 5;
  end

d06db example results

Example 1


 Transformation   1: translation
  translation vector:   1.000       0.000

 Final transformation matrix y = A*x + b:
    1.000       0.000          1.000
    0.000       1.000          0.000

 Transformation   1: translation
  translation vector:  0.7895      0.8947

 Final transformation matrix y = A*x + b:
    1.000       0.000         0.7895
    0.000       1.000         0.8947


Example 2

 The restitched mesh characteristics
 nv    =   643
 nelt  =  1133
 nedge =   171