NAG Toolbox: nag_pde_1d_blackscholes_closed (d03nd)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{kopt}$ – int64int32nag_int scalar

Specifies the kind of option to be valued:

$\mathbf{kopt}=1$

A European call option.

$\mathbf{kopt}=2$

An American call option.

$\mathbf{kopt}=3$

A European put option.

Constraints:

• $\mathbf{kopt}=1$, $2$ or $3$;
• if $q\ne 0$, $\mathbf{kopt}\ne 2$.

2:     $\mathrm{x}$ – double scalar

The exercise price $X$.

Constraint: $\mathbf{x}\ge 0.0$.

3:     $\mathrm{s}$ – double scalar

The stock price at which the option value and the Greeks should be evaluated.

Constraint: $\mathbf{s}\ge 0.0$.

4:     $\mathrm{t}$ – double scalar

The time at which the option value and the Greeks should be evaluated.

Constraint: $\mathbf{t}\ge 0.0$.

5:     $\mathrm{tmat}$ – double scalar

The maturity time of the option.

Constraint: $\mathbf{tmat}\ge \mathbf{t}$.

6:     $\mathrm{tdpar}\left(3\right)$ – logical array

Specifies whether or not various arguments are time-dependent. More precisely, $r$ is time-dependent if $\mathbf{tdpar}\left(1\right)=\mathit{true}$ and constant otherwise. Similarly, $\mathbf{tdpar}\left(2\right)$ specifies whether $q$ is time-dependent and $\mathbf{tdpar}\left(3\right)$ specifies whether $\sigma$ is time-dependent.

7:     $\mathrm{r}\left(:\right)$ – double array

The dimension of the array r must be at least $3$ if $\mathbf{tdpar}\left(1\right)=\mathit{true}$, and at least $1$ otherwise

If $\mathbf{tdpar}\left(1\right)=\mathit{false}$ then $\mathbf{r}\left(1\right)$ must contain the constant value of $r$. The remaining elements need not be set.

If $\mathbf{tdpar}\left(1\right)=\mathit{true}$ then $\mathbf{r}\left(1\right)$ must contain the value of $r$ at time t and $\mathbf{r}\left(2\right)$ must contain its average instantaneous value over the remaining life of the option:

$$\hat{r}=\underset{\mathbf{t}}{\overset{\mathbf{tmat}}{\int }}r\left(\zeta \right)d\zeta \text{.}$$

The auxiliary function nag_pde_1d_blackscholes_means (d03ne) may be used to construct r from a set of values of $r$ at discrete times.

8:     $\mathrm{q}\left(:\right)$ – double array

The dimension of the array q must be at least $3$ if $\mathbf{tdpar}\left(2\right)=\mathit{true}$, and at least $1$ otherwise

If $\mathbf{tdpar}\left(2\right)=\mathit{false}$ then $\mathbf{q}\left(1\right)$ must contain the constant value of $q$. The remaining elements need not be set.

If $\mathbf{tdpar}\left(2\right)=\mathit{true}$ then $\mathbf{q}\left(1\right)$ must contain the constant value of $q$ and $\mathbf{q}\left(2\right)$ must contain its average instantaneous value over the remaining life of the option:

$$\hat{q}=\underset{\mathbf{t}}{\overset{\mathbf{tmat}}{\int }}q\left(\zeta \right)d\zeta \text{.}$$

The auxiliary function nag_pde_1d_blackscholes_means (d03ne) may be used to construct q from a set of values of $q$ at discrete times.

9:     $\mathrm{sigma}\left(:\right)$ – double array

The dimension of the array sigma must be at least $3$ if $\mathbf{tdpar}\left(3\right)=\mathit{true}$, and at least $1$ otherwise

If $\mathbf{tdpar}\left(3\right)=\mathit{false}$ then $\mathbf{sigma}\left(1\right)$ must contain the constant value of $\sigma$. The remaining elements need not be set.

If $\mathbf{tdpar}\left(3\right)=\mathit{true}$ then $\mathbf{sigma}\left(1\right)$ must contain the value of $\sigma$ at time t, $\mathbf{sigma}\left(2\right)$ the average instantaneous value $\hat{\sigma }$, and $\mathbf{sigma}\left(3\right)$ the second-order average $\stackrel{-}{\sigma }$, where:

$$\hat{\sigma }=\underset{\mathbf{t}}{\overset{\mathbf{tmat}}{\int }}\sigma \left(\zeta \right)d\zeta \text{,}$$

$$\stackrel{-}{\sigma }={\left(\underset{\mathbf{t}}{\overset{\mathbf{tmat}}{\int }}{\sigma }^2\left(\zeta \right)d\zeta \right)}^{1/2}\text{.}$$

The auxiliary function nag_pde_1d_blackscholes_means (d03ne) may be used to compute sigma from a set of values at discrete times.

Constraints:

• if $\mathbf{tdpar}\left(3\right)=\mathit{false}$, $\mathbf{sigma}\left(1\right)>0.0$;
• if $\mathbf{tdpar}\left(3\right)=\mathit{true}$, $\mathbf{sigma}\left(\mathit{i}\right)>0.0$, for $\mathit{i}=1,2,3$.

Optional Input Parameters

None.

Output Parameters

1:     $\mathrm{f}$ – double scalar

The value $f$ of the option at the stock price s and time t.

2:     $\mathrm{theta}$ – double scalar

3:     $\mathrm{delta}$ – double scalar

4:     $\mathrm{gamma}$ – double scalar

5:     $\mathrm{lambda}$ – double scalar

6:     $\mathrm{rho}$ – double scalar

The values of various Greeks at the stock price s and time t, as follows:

$$\begin{array}{lll}\mathbf{theta}=\Theta =\frac{\partial f}{\partial t}\text{,}& \mathbf{delta}=\Delta =\frac{\partial f}{\partial \mathbf{s}}\text{,}& \mathbf{gamma}=\Gamma =\frac{{\partial }^{2}f}{\partial {\mathbf{s}}^2}\text{,}\\ & & \\ \mathbf{lambda}=\Lambda =\frac{\partial f}{\partial \sigma }\text{,}& \mathbf{rho}=\rho =\frac{\partial f}{\partial r}\text{.}& \end{array}$$

7:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

   $\mathbf{ifail}=1$

On entry,	$\mathbf{kopt}<1$,
or	$\mathbf{kopt}>3$,
or	$\mathbf{kopt}=2$ when $q\ne 0$,
or	$\mathbf{x}<0.0$,
or	$\mathbf{s}<0.0$,
or	$\mathbf{t}<0.0$,
or	$\mathbf{tmat}<\mathbf{t}$,
or	$\mathbf{sigma}\left(1\right)\le 0.0$, with $\mathbf{tdpar}\left(3\right)=\mathit{false}$,
or	$\mathbf{sigma}\left(i\right)\le 0.0$, with $\mathbf{tdpar}\left(3\right)=\mathit{true}$, for some $i=1$, $2$ or $3$.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Algorithmic Details

Example

Open in the MATLAB editor: d03nd_example

function d03nd_example


fprintf('d03nd example results\n\n');

% American 5-month call option, exercise price 50

kopt = int64(2);
x = 50;
ns    = 21;  nt    = 4;
s_beg = 0;   t_beg = 0;
s_end = 100; t_end = 0.125;
tmat  = 0.4166667;
tdpar = [false; false; false];
r     = [0.1];
q     = [0];
sigma = [0.4];

% Discretize s and t
ds = (s_end-s_beg)/(ns-1);
dt = (t_end-t_beg)/(nt-1);
s = [s_beg:ds:s_end];
t = [t_beg:dt:t_end];

f = zeros(ns,nt);
theta = f; delta = f; gamma = f; lambda = f; rho = f;

% Loop over times and prices
for j = 1:nt
  for i = 1:ns
    [f(i,j),theta(i,j),delta(i,j),gamma(i,j),lambda(i,j),rho(i,j),ifail] = ...
    d03nd( ...
           kopt, x, s(i), t(j), tmat, tdpar, r, q, sigma);
  end
end

% Tabulate option values only
print_greek(ns,nt,tmat,s,t,'Option Values',f);
% print_greek(ns,nt,tmat,s,t,'Theta',theta);
% print_greek(ns,nt,tmat,s,t,'Delta',delta);
% print_greek(ns,nt,tmat,s,t,'Gamma',gamma);
% print_greek(ns,nt,tmat,s,t,'Lambda',lambda);
% print_greek(ns,nt,tmat,s,t,'Rho',rho);

% plot initial and final option values and greeks 
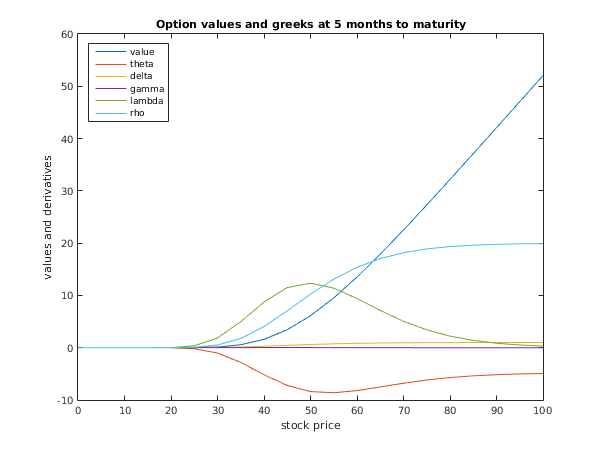
fig1 = figure;
plot(s,f(:,1),s,theta(:,1),s,delta(:,1),s,gamma(:,1),s,lambda(:,1),s,rho(:,1));
legend('value','theta','delta','gamma','lambda','rho','Location','NorthWest');
title('Option values and greeks at 5 months to maturity');
xlabel('stock price');
ylabel('values and derivatives');
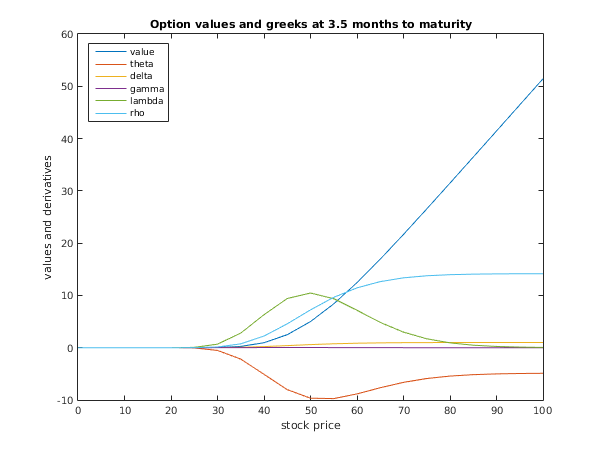
fig2 = figure;
plot(s,f(:,4),s,theta(:,4),s,delta(:,4),s,gamma(:,4),s,lambda(:,4),s,rho(:,4));
legend('value','theta','delta','gamma','lambda','rho','Location','NorthWest');
title('Option values and greeks at 3.5 months to maturity');
xlabel('stock price');
ylabel('values and derivatives');



function print_greek(ns,nt,tmat,s,t,grname,greek)

  fprintf('\n%s\n\n',grname);
  fprintf('  Stock Price  |   Time to Maturity (months)\n');
  fprintf('%16s %12.4e%12.4e%12.4e%12.4e\n', '|', 12*(tmat-t));
  fprintf('%15s+%48s\n', '---------------', ...
          '-------------------------------------------------');
  for i = 1:ns
    fprintf('%12.4e%4s %12.4e%12.4e%12.4e%12.4e\n', s(i), '|', greek(i,:));
  end

d03nd example results


Option Values

  Stock Price  |   Time to Maturity (months)
               |   5.0000e+00  4.5000e+00  4.0000e+00  3.5000e+00
---------------+-------------------------------------------------
  0.0000e+00   |   0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00
  5.0000e+00   |   4.4491e-19  4.5989e-21  1.5461e-23  1.0478e-26
  1.0000e+01   |   5.5566e-10  5.5129e-11  3.1298e-12  8.0281e-14
  1.5000e+01   |   4.7337e-06  1.2187e-06  2.2774e-07  2.7003e-08
  2.0000e+01   |   7.2236e-04  3.1054e-04  1.1005e-04  2.9678e-05
  2.5000e+01   |   1.6557e-02  9.6610e-03  5.0099e-03  2.2012e-03
  3.0000e+01   |   1.3307e-01  9.4037e-02  6.1869e-02  3.6848e-02
  3.5000e+01   |   5.6631e-01  4.5257e-01  3.4667e-01  2.5053e-01
  4.0000e+01   |   1.6004e+00  1.3850e+00  1.1699e+00  9.5640e-01
  4.5000e+01   |   3.4384e+00  3.1328e+00  2.8168e+00  2.4891e+00
  5.0000e+01   |   6.1165e+00  5.7600e+00  5.3874e+00  4.9960e+00
  5.5000e+01   |   9.5300e+00  9.1645e+00  8.7846e+00  8.3882e+00
  6.0000e+01   |   1.3509e+01  1.3163e+01  1.2808e+01  1.2445e+01
  6.5000e+01   |   1.7883e+01  1.7568e+01  1.7251e+01  1.6932e+01
  7.0000e+01   |   2.2513e+01  2.2230e+01  2.1949e+01  2.1671e+01
  7.5000e+01   |   2.7301e+01  2.7045e+01  2.6792e+01  2.6544e+01
  8.0000e+01   |   3.2182e+01  3.1946e+01  3.1713e+01  3.1485e+01
  8.5000e+01   |   3.7117e+01  3.6894e+01  3.6674e+01  3.6458e+01
  9.0000e+01   |   4.2081e+01  4.1868e+01  4.1656e+01  4.1446e+01
  9.5000e+01   |   4.7062e+01  4.6854e+01  4.6647e+01  4.6441e+01
  1.0000e+02   |   5.2052e+01  5.1847e+01  5.1643e+01  5.1439e+01