PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_pde_2d_ellip_discret (d03ee)
Purpose
nag_pde_2d_ellip_discret (d03ee) discretizes a second-order elliptic partial differential equation (PDE) on a rectangular region.
Syntax
[
a,
rhs,
ifail] = d03ee(
xmin,
xmax,
ymin,
ymax,
pdef,
bndy,
ngx,
ngy,
scheme)
[
a,
rhs,
ifail] = nag_pde_2d_ellip_discret(
xmin,
xmax,
ymin,
ymax,
pdef,
bndy,
ngx,
ngy,
scheme)
Description
nag_pde_2d_ellip_discret (d03ee) discretizes a second-order linear elliptic partial differential equation of the form
on a rectangular region
subject to boundary conditions of the form
where
denotes the outward pointing normal derivative on the boundary. Equation
(1) is said to be elliptic if
for all points in the rectangular region. The linear equations produced are in a form suitable for passing directly to the multigrid function
nag_pde_2d_ellip_mgrid (d03ed).
The equation is discretized on a rectangular grid, with
grid points in the
-direction and
grid points in the
-direction. The grid spacing used is therefore
and the coordinates of the grid points
are
At each grid point
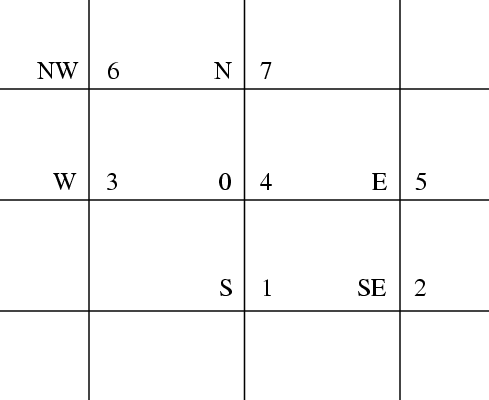
six neighbouring grid points are used to approximate the partial differential equation, so that the equation is discretized on the seven-point stencil shown in
Figure 1.
For convenience the approximation to the exact solution is denoted by , and the neighbouring approximations are labelled according to points of the compass as shown. Where numerical labels for the seven points are required, these are also shown.
The following approximations are used for the second derivatives:
Two possible schemes may be used to approximate the first derivatives:
Central differences are more accurate than upwind differences, but upwind differences may lead to a more diagonally dominant matrix for those problems where the coefficients of the first derivatives are significantly larger than the coefficients of the second derivatives.
The approximations used for the first derivatives may be written in a more compact form as follows:
where
and
for upwind differences, and
for central differences.
At all points in the rectangular domain, including the boundary, the coefficients in the partial differential equation are evaluated by calling
pdef, and applying the approximations. This leads to a seven-diagonal system of linear equations of the form:
where the coefficients are given by
These equations then have to be modified to take account of the boundary conditions. These may be Dirichlet (where the solution is given), Neumann (where the derivative of the solution is given), or mixed (where a linear combination of solution and derivative is given).
If the boundary conditions are Dirichlet, there are an infinity of possible equations which may be applied:
If
nag_pde_2d_ellip_mgrid (d03ed) is used to solve the discretized equations, it turns out that the choice of
can have a dramatic effect on the rate of convergence, and the obvious choice
is not the best. Some choices may even cause the multigrid method to fail altogether. In practice it has been found that a value of the same order as the other diagonal elements of the matrix is best, and the following value has been found to work well in practice:
If the boundary conditions are either mixed or Neumann (i.e.,
on return from
bndy), then one of the points in the seven-point stencil lies outside the domain. In this case the normal derivative in the boundary conditions is used to eliminate the ‘fictitious’ point,
:
It should be noted that if the boundary conditions are Neumann and , then there is no unique solution. The function returns with in this case, and the seven-diagonal matrix is singular.
The four corners are treated separately.
bndy is called twice, once along each of the edges meeting at the corner. If both boundary conditions at this point are Dirichlet and the prescribed solution values agree, then this value is used in an equation of the form
(2). If the prescribed solution is discontinuous at the corner, then the average of the two values is used. If one boundary condition is Dirichlet and the other is mixed, then the value prescribed by the Dirichlet condition is used in an equation of the form given above. Finally, if both conditions are mixed or Neumann, then two ‘fictitious’ points are eliminated using two equations of the form
(3).
It is possible that equations for which the solution is known at all points on the boundary, have coefficients which are not defined on the boundary. Since this function calls
pdef at
all points in the domain, including boundary points, arithmetic errors may occur in
pdef which this function cannot trap. If you have an equation with Dirichlet boundary conditions (i.e.,
at all points on the boundary), but with PDE coefficients which are singular on the boundary, then
nag_pde_2d_ellip_mgrid (d03ed) could be called directly only using interior grid points at your discretization.
After the equations have been set up as described above, they are checked for diagonal dominance. That is to say,
If this condition is not satisfied then the function returns with
. The multigrid function
nag_pde_2d_ellip_mgrid (d03ed) may still converge in this case, but if the coefficients of the first derivatives in the partial differential equation are large compared with the coefficients of the second derivative, you should consider using upwind differences (
).
Since this function is designed primarily for use with
nag_pde_2d_ellip_mgrid (d03ed), this document should be read in conjunction with the document for that function.
References
Wesseling P (1982) MGD1 – a robust and efficient multigrid method Multigrid Methods. Lecture Notes in Mathematics 960 614–630 Springer–Verlag
Parameters
Compulsory Input Parameters
- 1:
– double scalar
- 2:
– double scalar
-
The lower and upper coordinates of the rectangular region respectively, and .
Constraint:
.
- 3:
– double scalar
- 4:
– double scalar
-
The lower and upper coordinates of the rectangular region respectively, and .
Constraint:
.
- 5:
– function handle or string containing name of m-file
-
pdef must evaluate the functions
,
,
,
,
,
and
which define the equation at a general point
.
[alpha, beta, gamma, delta, epslon, phi, psi] = pdef(x, y)
Input Parameters
- 1:
– double scalar
- 2:
– double scalar
-
The and coordinates of the point at which the coefficients of the partial differential equation are to be evaluated.
Output Parameters
- 1:
– double scalar
- 2:
– double scalar
- 3:
– double scalar
- 4:
– double scalar
- 5:
– double scalar
- 6:
– double scalar
- 7:
– double scalar
-
alpha,
beta,
gamma,
delta,
epslon,
phi and
psi must be set to the values of
,
,
,
,
,
and
respectively at the point specified by
x and
y.
- 6:
– function handle or string containing name of m-file
-
bndy must evaluate the functions
,
, and
involved in the boundary conditions.
[a, b, c] = bndy(x, y, ibnd)
Input Parameters
- 1:
– double scalar
- 2:
– double scalar
-
The and coordinates of the point at which the boundary conditions are to be evaluated.
- 3:
– int64int32nag_int scalar
-
Specifies on which boundary the point (
x,
y) lies.
,
,
or
according as the point lies on the bottom, right, top or left boundary.
Output Parameters
- 1:
– double scalar
- 2:
– double scalar
- 3:
– double scalar
-
a,
b and
c must be set to the values of the functions appearing in the boundary conditions.
- 7:
– int64int32nag_int scalar
- 8:
– int64int32nag_int scalar
-
The number of interior grid points in the
- and
-directions respectively,
and
. If the seven-diagonal equations are to be solved by
nag_pde_2d_ellip_mgrid (d03ed), then
and
should preferably be divisible by as high a power of
as possible.
- 9:
– string (length ≥ 1)
-
The type of approximation to be used for the first derivatives which occur in the partial differential equation.
- Central differences are used.
- Upwind differences are used.
Constraint:
or
.
Note: generally speaking, if at least one of the coefficients multiplying the first derivatives (
delta or
epslon as returned by
pdef) are large compared with the coefficients multiplying the second derivatives, then upwind differences may be more appropriate. Upwind differences are less accurate than central differences, but may result in more rapid convergence for strongly convective equations. The easiest test is to try both schemes.
Optional Input Parameters
None.
Output Parameters
- 1:
– double array
-
, for
and
, contains the seven-diagonal linear equations produced by the discretization described above. If
, the remaining elements are not referenced by the function, but if
then the array
a can be passed directly to
nag_pde_2d_ellip_mgrid (d03ed), where these elements are used as workspace.
- 2:
– double array
-
The first
elements contain the right-hand sides of the seven-diagonal linear equations produced by the discretization described above. If
, the remaining elements are not referenced by the function, but if
then the array
rhs can be passed directly to
nag_pde_2d_ellip_mgrid (d03ed), where these elements are used as workspace.
- 3:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Note: nag_pde_2d_ellip_discret (d03ee) may return useful information for one or more of the following detected errors or warnings.
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
| On entry, | , |
| or | , |
| or | , |
| or | , |
| or | , |
| or | scheme is not one of 'C' or 'U'. |
-
-
At some point on the boundary there is a derivative in the boundary conditions (
on return from
bndy) and there is a nonzero coefficient of the mixed derivative
(
on return from
pdef).
-
-
A null boundary has been specified, i.e., at some point both
a and
b are zero on return from a call to
bndy.
- W
-
The equation is not elliptic, i.e.,
after a call to
pdef. The discretization has been completed, but the convergence of
nag_pde_2d_ellip_mgrid (d03ed) cannot be guaranteed.
- W
-
The boundary conditions are purely Neumann (only the derivative is specified) and there is, in general, no unique solution.
- W
-
The equations were not diagonally dominant. (See
Description.)
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
Not applicable.
Further Comments
If this function is used as a preprocessor to the multigrid function
nag_pde_2d_ellip_mgrid (d03ed) it should be noted that the rate of convergence of that function is strongly dependent upon the number of levels in the multigrid scheme, and thus the choice of
ngx and
ngy is very important.
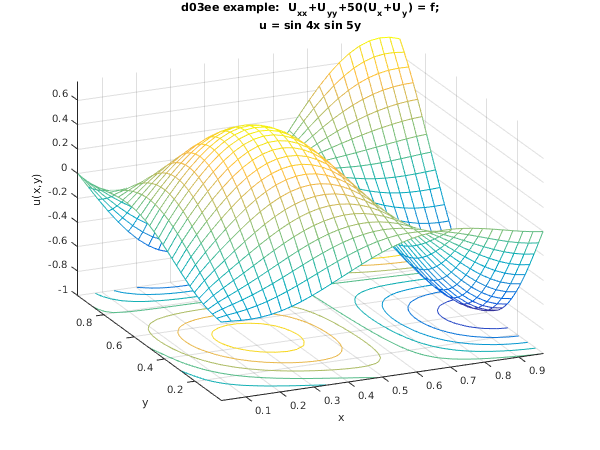
Example
The program solves the elliptic partial differential equation
on the unit square
,
, with boundary conditions
- given on and ,
- given on and .
The function and the exact form of the boundary conditions are derived from the exact solution .
The equation is first solved using central differences. Since the coefficients of the first derivatives are large, the linear equations are not diagonally dominated, and convergence is slow. The equation is solved a second time with upwind differences, showing that convergence is more rapid, but the solution is less accurate.
Open in the MATLAB editor:
d03ee_example
function d03ee_example
fprintf('d03ee example results\n\n');
global k l;
k = 4; l = 5;
xmin = 0; xmax = 1;
ymin = 0; ymax = 1;
ngx = int64(33); ngy = ngx;
scheme = 'Upwind';
[a, rhs, ifail] = ...
d03ee( ...
xmin, xmax, ymin, ymax, @pdef, @bndy, ngx, ngy, scheme);
maxit = int64(100); acc = 0.0001; iout = int64(0);
ub = zeros(ngx*ngy, 1);
[a, rhs, ub, resid, u, numit, ifail] = ...
d03ed( ...
ngx, ngy, a, rhs, ub, maxit, acc, iout);
fprintf('Number of iterations to solution = %2d.\n', numit);
fprintf('Maximum residual %8.1e\n',resid(numit));
u2 = u(1:ngx*ngy);
umat = reshape(u2,ngx,ngy);
hx = 1/double(ngx+1);
hy = hx;
x(1:ngx) = hx:hx:1-hx;
y(1:ngy) = hy:hy:1-hy;
[xs,ys] = meshgrid(y,x);
fig1 = figure;
meshc(xs,ys,umat);
xlabel('x'); ylabel('y'); zlabel ('u(x,y)');
exact = sprintf('u = sin %dx sin %dy',k,l);
title({'d03ee example: U_{xx}+U_{yy}+50(U_x+U_y) = f;',exact});
view(-24,28);
function [alpha, beta, gamma, delta, epsilon, phi, psi] = pdef(x,y)
global k l;
u = sin(k*x)*cos(l*y);
ux = k*cos(k*x)*sin(l*y); uy = l*sin(k*x)*cos(l*y);
uxx = -k*k*u; uyy = -l*l*u;
uxy = k*l*cos(k*x)*cos(l*y);
alpha = 1; beta = 0; gamma = 1; delta = 50; epsilon = 50;
phi = 0;
psi = alpha*uxx + beta*uxy + gamma*uyy + delta*ux + epsilon*uy + phi*u;
function [a, b, c] = bndy(x, y, ibnd)
global k l;
u = sin(k*x)*sin(l*y);
if (ibnd == 2 || ibnd == 1)
a = 1;
b = 0;
c = u;
elseif (ibnd == 0)
a = 0;
b = 1;
c = -l*sin(k*x);
elseif (ibnd == 3)
a = 0;
b = 1;
c = -k*sin(l*y);
end
d03ee example results
Number of iterations to solution = 5.
Maximum residual -3.4e-09
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015