PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_pde_2d_ellip_mgrid (d03ed)
Purpose
nag_pde_2d_ellip_mgrid (d03ed) solves seven-diagonal systems of linear equations which arise from the discretization of an elliptic partial differential equation on a rectangular region. This function uses a multigrid technique.
Syntax
[
a,
rhs,
ub,
us,
u,
numit,
ifail] = d03ed(
ngx,
ngy,
a,
rhs,
ub,
maxit,
acc,
iout)
[
a,
rhs,
ub,
us,
u,
numit,
ifail] = nag_pde_2d_ellip_mgrid(
ngx,
ngy,
a,
rhs,
ub,
maxit,
acc,
iout)
Description
nag_pde_2d_ellip_mgrid (d03ed) solves, by multigrid iteration, the seven-point scheme
which arises from the discretization of an elliptic partial differential equation of the form
and its boundary conditions, defined on a rectangular region. This we write in matrix form as
The algorithm is described in separate reports by
Wesseling (1982a),
Wesseling (1982b) and
McCarthy (1983).
Systems of linear equations, matching the seven-point stencil defined above, are solved by a multigrid iteration. An initial estimate of the solution must be provided by you. A zero guess may be supplied if no better approximation is available.
A ‘smoother’ based on incomplete Crout decomposition is used to eliminate the high frequency components of the error. A restriction operator is then used to map the system on to a sequence of coarser grids. The errors are then smoothed and prolongated (mapped onto successively finer grids). When the finest cycle is reached, the approximation to the solution is corrected. The cycle is repeated for
maxit iterations or until the required accuracy,
acc, is reached.
nag_pde_2d_ellip_mgrid (d03ed) will automatically determine the number
of possible coarse grids, ‘levels’ of the multigrid scheme, for a particular problem. In other words,
nag_pde_2d_ellip_mgrid (d03ed) determines the maximum integer
so that
and
can be expressed in the form
It should be noted that the rate of convergence improves significantly with the number of levels used (see
McCarthy (1983)), so that
and
should be carefully chosen so that
and
have factors of the form
, with
as large as possible. For good convergence the integer
should be at least
.
nag_pde_2d_ellip_mgrid (d03ed) has been found to be robust in application, but being an iterative method the problem of divergence can arise. For a strictly diagonally dominant matrix
no such problem is foreseen. The diagonal dominance of
is not a necessary condition, but should this condition be strongly violated then divergence may occur. The quickest test is to try the function.
References
McCarthy G J (1983) Investigation into the multigrid code MGD1 Report AERE-R 10889 Harwell
Wesseling P (1982a) MGD1 – a robust and efficient multigrid method Multigrid Methods. Lecture Notes in Mathematics 960 614–630 Springer–Verlag
Wesseling P (1982b) Theoretical aspects of a multigrid method SIAM J. Sci. Statist. Comput. 3 387–407
Parameters
Compulsory Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of interior grid points in the -direction, . should preferably be divisible by as high a power of as possible.
Constraint:
.
- 2:
– int64int32nag_int scalar
-
The number of interior grid points in the -direction, . should preferably be divisible by as high a power of as possible.
Constraint:
.
- 3:
– double array
-
must be set to , for , and .
- 4:
– double array
-
must be set to , for and .
- 5:
– double array
-
must be set to the initial estimate for the solution .
- 6:
– int64int32nag_int scalar
-
The maximum permitted number of multigrid iterations. If
, no multigrid iterations are performed, but the coarse-grid approximations and incomplete Crout decompositions are computed, and may be output if
iout is set accordingly.
Constraint:
.
- 7:
– double scalar
-
The required tolerance for convergence of the residual
-norm:
where
and
is the computed solution. Note that the norm is not scaled by the number of equations. The function will stop after fewer than
maxit iterations if the residual
-norm is less than the specified tolerance. (If
, at least one iteration is always performed.)
If on entry
, then the
machine precision is used as a default value for the tolerance; if
, but
acc is less than the
machine precision, then the function will stop when the residual
-norm is less than the
machine precision and
ifail will be set to
.
Constraint:
.
- 8:
– int64int32nag_int scalar
-
Controls the output of printed information to the advisory message unit as returned by
nag_file_set_unit_advisory (x04ab):
- No output.
- The solution
, for and .
- The residual -norm after each iteration, with the reduction factor over the previous iteration.
- As for and .
- As for , plus the final residual (as returned in ub).
- As for , plus the initial elements of a and rhs.
- As for , plus the Galerkin coarse grid approximations.
- As for , plus the incomplete Crout decompositions.
- As for , plus the residual after each iteration.
The elements
, the Galerkin coarse grid approximations and the incomplete Crout decompositions are output in the format:
- Y-index
- X-index
- where
, for and .
The vectors
,
,
are output in matrix form with
ngy rows and
ngx columns. Where
, the
ngx values for a given
value are produced in rows of
. Values of
may yield considerable amounts of output.
Constraint:
.
Optional Input Parameters
None.
Output Parameters
- 1:
– double array
-
Is overwritten.
- 2:
– double array
-
The first elements are unchanged and the rest of the array is used as workspace.
- 3:
– double array
-
The corresponding component of the residual .
- 4:
– double array
-
The residual -norm, stored in element .
- 5:
– double array
-
The computed solution is returned in , for and .
- 6:
– int64int32nag_int scalar
-
The number of iterations performed.
- 7:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
| On entry, | , |
| or | , |
| or | lda is too small, |
| or | , |
| or | , |
| or | , |
| or | . |
-
-
maxit iterations have been performed with the residual
-norm decreasing at each iteration but the residual
-norm has not been reduced to less than the specified tolerance (see
acc). Examine the progress of the iteration by setting
.
-
-
As for , except that at one or more iterations the residual -norm did not decrease. It is likely that the method fails to converge for the given matrix .
- W
-
On entry,
acc is less than the
machine precision. The function terminated because the residual norm is less than the
machine precision.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
Further Comments
The rate of convergence of this function is strongly dependent upon the number of levels,
, in the multigrid scheme, and thus the choice of
ngx and
ngy is very important. You are advised to experiment with different values of
ngx and
ngy to see the effect they have on the rate of convergence; for example, using a value such as
(
) followed by
(for which
).
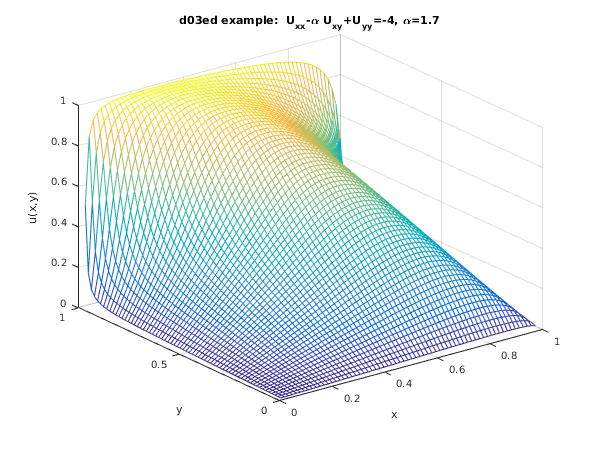
Example
The program solves the elliptic partial differential equation
on the unit square
, with boundary conditions
For the equation to be elliptic,
must be less than
.
The equation is discretized on a square grid with mesh spacing
in both directions using the following approximations:
Thus the following equations are solved:
Open in the MATLAB editor:
d03ed_example
function d03ed_example
fprintf('d03ed example results\n\n');
ngx = int64(65);
ngy = ngx;
nn = ngx*ngy;
lda = 4*(ngx+1)*(ngy+1)/3;
a = zeros(lda,7);
rhs = zeros(lda, 1);
ub = zeros(nn, 1);
maxit = int64(15); acc = 0.0001; iout = int64(0);
hx = 1/double(ngx+1);
hy = 1/double(ngy+1);
alpha = 1.7;
a(1:nn,[1 3 5 7]) = 1 - 0.5*alpha;
a(1:nn,[2 6]) = 0.5*alpha;
a(1:nn,4) = -4 + alpha;
rhs(1:nn) = -4*hx*hy;
a(2:ngx-1,1:2) = 0.0;
a(nn-ngx+2:nn-1,6:7) = 0.0;
for j = 2:ngy-1
iy = (j-1)*ngx + 1;
a(iy,[3 6]) = 0.0;
iy = j*ngx;
rhs(iy) = rhs(iy) - a(iy,5) - a(iy,2);
a(iy,[2 5]) = 0.0;
end
a(1,[1:3 6]) = 0.0;
k = nn - ngx + 1;
a(k,[3 6:7]) = 0.0;
k = ngx;
rhs(k) = rhs(k) - a(k,2)*0.5 - a(k,5);
a(k,[1:2 5]) = 0.0;
k = ngx*ngy;
rhs(k) = rhs(k) - a(k,2) - a(k,5);
a(k,[2 5:7]) = 0.0;
u = zeros(ngx*ngy,1);
[a, rhs, ub, resid, u, numit, ifail] = ...
d03ed(...
ngx, ngy, a, rhs, ub, maxit, acc, iout);
fprintf('Number of iterations %4d\n',numit);
fprintf('Maximum residual %8.3e\n',resid(numit));
fig1 = figure;
u2 = u(1:nn);
umat = reshape(u2,ngx,ngy);
x(1:ngx) = hx:hx:1-hx; y(1:ngy) = hy:hy:1-hy;
[xs,ys] = meshgrid(y,x);
mesh(xs,ys,umat);
xlabel('x'); ylabel('y'); zlabel ('u(x,y)');
title('d03ed example: U_{xx}-\alpha U_{xy}+U_{yy}=-4, \alpha=1.7');
d03ed example results
Number of iterations 4
Maximum residual -1.060e-08
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015