| At Mark 22: | lrwork and liwork were removed from the interface |
None.
Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.
Open in the MATLAB editor: d02qz_example
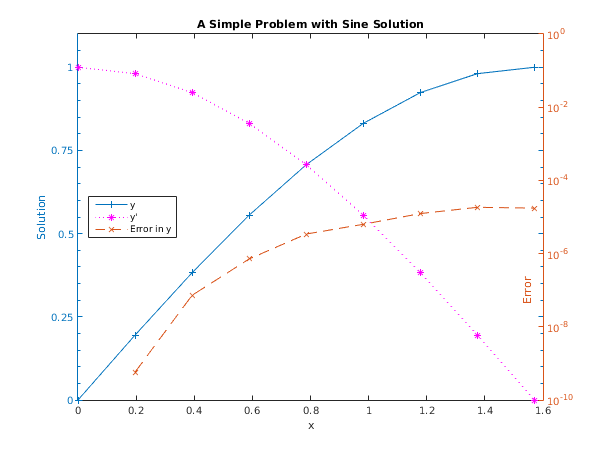
function d02qz_example fprintf('d02qz example results\n\n'); % Initialize variables and arrays. neqf = int64(2); neqg = int64(0); latol = neqf; lrtol = neqf; lrwork = 23 + 23*neqf + 14*neqg; liwork = 21 + 4*neqg; rwork = zeros(lrwork); iwork = zeros(liwork,'int64'); tstart = 0; hmax = 2.0; statef = 's'; vectol = true; alterg = false; sophst = false; atol = [1.0e-08; 1.0e-08]; rtol = [1.0e-04; 1.0e-04]; onestp = true; crit = true; tinc = 0.0625*pi; tcrit = 8.0*tinc; tout = tcrit; maxstp = int64(500); t = tstart; twant = tstart + tinc; nwant = neqf; y = [0 1]; % d02qw is a setup routine to be called prior to d02qf. [statef, alterg, rwork, iwork, ifail] = ... d02qw( ... statef, neqf, vectol, atol, rtol, onestp, crit, tcrit, hmax, ... maxstp, neqg, alterg, sophst, rwork, iwork); % Prepare to store results for plotting. xarray = zeros(1); yarray = zeros(1, neqf+1); % Output initial results. fprintf(' t y_1 y_2\n'); fprintf('%6.4f %7.4f %7.4f\n', t, y(1:2)); xarray(1) = t; yarray(1, 1:neqf) = y(1:neqf); j = 1; while t < tout % Integrate ODEs from t to tout. [t, y, root, rwork, iwork, ifail] = ... d02qf( ... @f, t, y, tout, 'd02qfz', neqg, rwork, iwork); % Now interpolate the solution at twant; keep looping till % twant is bigger than t. while twant <= t [ywant, ypwant, ifail] = ... d02qz( ... neqf, twant, nwant, rwork, iwork); fprintf('%6.4f %7.4f %7.4f\n', twant, ywant(1), ywant(2)); j = j+1; xarray(j) = twant; yarray(j, neqf+1) = abs(ywant(1) - sin(twant)); yarray(j, 1:neqf) = ywant(1:neqf); twant = tstart + j*tinc; end end % Plot results. fig1 = figure; display_plot(xarray, yarray); function f = f(neqf, x, y) % Evaluate derivative vector. f = zeros(neqf, 1); f(1) = y(2); f(2) = -y(1); function display_plot(x, y) % Plot two of the curves, then add the other one. [haxes, hline1, hline2] = plotyy(x, y(:,1), x, y(:,3), 'plot', 'semilogy'); % We want the third curve to be plotted on the left-hand y-axis. hold(haxes(1), 'on'); hline3 = plot(x, y(:,2)); % Set the axis limits and the tick specifications to beautify the plot. set(haxes(1), 'YLim', [0 1.1]); set(haxes(1), 'YMinorTick', 'on'); set(haxes(1), 'YTick', [0.0 0.25 0.5 0.75 1.0]); set(haxes(2), 'YMinorTick', 'on'); set(haxes(2), 'YTick', [1.0e-10 1.0e-8 1.0e-6 1.0e-4 1.0e-2 1.0]); for iaxis = 1:2 % These properties must be the same for both sets of axes. set(haxes(iaxis), 'XLim', [0 1.6]); end % Add title. title('A Simple Problem with Sine Solution'); % Label the axes. xlabel('x'); ylabel(haxes(1), 'Solution'); yh2 = ylabel(haxes(2), 'Error'); set(yh2,'position',[1.52,1e-7]); % Add a legend. legend('y','y''','Error in y','Location','West') % Set some features of the three lines. set(hline1, 'Linewidth', 0.25, 'Marker', '+', 'LineStyle', '-'); set(hline2, 'Linewidth', 0.25, 'Marker', 'x', 'LineStyle', '--'); set(hline3, 'Linewidth', 0.25, 'Marker', '*', 'LineStyle', ':', ... 'Color', 'Magenta');
d02qz example results t y_1 y_2 0.0000 0.0000 1.0000 0.1963 0.1951 0.9808 0.3927 0.3827 0.9239 0.5890 0.5556 0.8315 0.7854 0.7071 0.7071 0.9817 0.8315 0.5556 1.1781 0.9239 0.3827 1.3744 0.9808 0.1951 1.5708 1.0000 -0.0000
